.gif)
Geon (psychology)
Encyclopedia
Geons are the simple 2D or 3D forms such as cylinders, bricks
, wedge
s, cones
, circles and rectangle
s corresponding to the simple parts of an object in Biederman's theory of object recognition
. The theory proposes that the visual input is matched against structural representations of objects in the brain
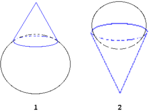
. These structural representations consist of geons and their relations (e.g., an ice cream cone
could be broken down into a sphere
located above a cone
). Only a modest number of geons (< 40) are assumed. When combined in different relations to each other (e.g., on-top-of, larger-than, end-to-end, end-to-middle) and coarse metric variation such as aspect ratio and 2D orientation, billions of possible 2- and 3-geon objects can be generated. Two classes of shape-based visual identification that are not done through geon representations, are those involved in: a) individuating similar faces, and b) classifications that don’t have definite boundaries, such as that of bushes or a crumpled garment. Typically, such identifications are not viewpoint-invariant.
 There are 4 essential properties of geons:
There are 4 essential properties of geons:
NAPs can be distinguished from metric properties (MPs), such as the degree of non-zero curvature of a contour or its length, which do vary with changes in orientation in depth.
These variations in the generating of geons create shapes that differ in NAPs.
Bricks
Bricks may refer to:* Brick, an artificial stone made by forming clay into rectangular blocks* Brick , a slang term for a device that cannot function due to internal failure...
, wedge
Wedge
Wedge may refer to:Mathematics:* Triangular prism, a parallel triangle wedge* Wedge , a polyhedral solid defined by two triangles and three trapezoid faces* Wedge product, a mathematical term, named for the ∧ operator symbol used...
s, cones
Cone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
, circles and rectangle
Rectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
s corresponding to the simple parts of an object in Biederman's theory of object recognition
Object recognition
Object recognition in computer vision is the task of finding a given object in an image or video sequence. Humans recognize a multitude of objects in images with little effort, despite the fact that the image of the objects may vary somewhat in different view points, in many different sizes / scale...
. The theory proposes that the visual input is matched against structural representations of objects in the brain
Brain
The brain is the center of the nervous system in all vertebrate and most invertebrate animals—only a few primitive invertebrates such as sponges, jellyfish, sea squirts and starfishes do not have one. It is located in the head, usually close to primary sensory apparatus such as vision, hearing,...
. These structural representations consist of geons and their relations (e.g., an ice cream cone
Ice cream cone
An ice cream cone, poke or cornet is a dry, cone-shaped pastry, usually made of a wafer similar in texture to a waffle, allowing ice cream to be eaten without a bowl or spoon...
could be broken down into a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
located above a cone
Cone
A cone is a basic geometrical shape; see cone .Cone may also refer to:-Mathematics:*Cone , a family of morphisms resembling a geometric cone...
). Only a modest number of geons (< 40) are assumed. When combined in different relations to each other (e.g., on-top-of, larger-than, end-to-end, end-to-middle) and coarse metric variation such as aspect ratio and 2D orientation, billions of possible 2- and 3-geon objects can be generated. Two classes of shape-based visual identification that are not done through geon representations, are those involved in: a) individuating similar faces, and b) classifications that don’t have definite boundaries, such as that of bushes or a crumpled garment. Typically, such identifications are not viewpoint-invariant.
Properties of Geons

- View-invariance: Each geon can be distinguished from the others from almost any viewpoints except for “accidents” at highly restricted angles in which one geon projects an image that could be a different geon, as, for example, when an end-on view of a cylinder can be a sphere or circle. Objects represented as an arrangement of geons would, similarly, be viewpoint invariant.
- Stability or Resistance to visual noise: Because the geons are simple they are readily supported by the Gestalt property of smooth continuation, rendering their identification robust to partial occlusion and degradation by visual noise as, for example, when a cylinder might be viewed behind a bush.
- Invariance to illumination direction and surface markings and texture.
- High distinctiveness: The geons differ qualitatively, with only two or three levels of an attributes, such as straight vs. curved, parallel vs. non parallel, positive vs. negative curvature. These qualitative differences can be readily distinguished thus rendering the geons readily distinguishable and the objects so composed, readily distinguishable.
Derivation of Invariant Properties of Geons
Viewpoint Invariance: The viewpoint invariance of geons derives from their being distinguished by three nonaccidental properties (NAPs) of contours that do not change with orientation in depth:- Whether the contour is straight or curved,
- The vertex that is formed when two or three contours coterminate (that is, end together at the same point), in the image, i.e., an L (2 contours), fork (3 contours with all angles < 180º), or an arrow (3 contours, with one angle > 180º), and
- Whether a pair of contours is parallel or not (with allowance for perspective). When not parallel, the contours can be straight (converging or diverging) or curved, with positive or negative curvature forming a convex or concave, envelope, respectively (see Figure below).
NAPs can be distinguished from metric properties (MPs), such as the degree of non-zero curvature of a contour or its length, which do vary with changes in orientation in depth.
Invariance to Lighting Direction and Surface Characteristics
Geons can be determined from the contours that mark the edges at orientation and depth discontinuities of an image of an object, i.e., the contours that specify a good line drawing of the object’s shape or volume. Orientation discontinuities define those edges where there is a sharp change in the orientation of the normal to the surface of a volume, as occurs at the contour at the boundaries of the different sides of a brick. A depth discontinuity is where the observer’s line of sight jumps from the surface of an object to the background (i.e., is tangent to the surface), as occurs at the sides of a cylinder. The same contour might mark both an orientation and depth discontinuity, as with the back edge of a brick. Because the geons are based on these discontinuities, they are invariant to variations in the direction of lighting, shadows, and surface texture and markings.Geons and Generalized Cones
The geons constitute a partition of the set of generalized cones, which are the volumes created when a cross section is swept along an axis. For example, a circle swept along a straight axis would define a cylinder. A rectangle swept along an axis would define a brick. Four dimensions with contrastive values (i.e., mutually exclusive values) define the current set of geons (see Figure):- Shape of cross section: round vs. straight.
- Axis: Straight vs. curved.
- Size of cross-section as it is swept along an axis: constant vs. expanding (or contracting) vs. expanding then contracting vs. contracting then expanding.
- Termination of geon with constant sized cross-sections: truncated vs. converging to a point vs. rounded.
These variations in the generating of geons create shapes that differ in NAPs.

