Best linear unbiased prediction
Encyclopedia
In statistics
, best linear unbiased prediction (BLUP) is used in linear mixed model
s for the estimation of random effects. BLUP was derived by Charles Roy Henderson
in 1950 but the term "best linear unbiased predictor" (or "prediction") seems not to have been used until 1962. "Best linear unbiased predictions" (BLUPs) of random effects are similar to best linear unbiased estimates (BLUEs) (see Gauss–Markov theorem
) of fixed effects. The distinction arises because it is conventional to talk about estimating fixed effects but predicting random effects, but the two terms are otherwise equivalent. (This is a bit strange since the random effects have already been "realized" − they already exist. The use of the term "prediction" may be because in the field of animal breeding in which Henderson worked, the random effects were usually genetic merit, which could be used to predict the quality of offspring. (Robinson page 28)) However, the equations for the "fixed" effects and for the random effects are different.
In practice, it is often the case that the parameters associated with the random effect(s) term(s) are unknown; these parameters are the variances of the random effects and residuals. Typically the parameters are estimated and plugged into the predictor, leading to the Empirical Best Linear Unbiased Predictor (EBLUP). Notice that by simply plugging in the estimated parameter into the predictor, additional variability is unaccounted for, leading to overly optimistic prediction variances for the EBLUP.
Best linear unbiased predictions are similar to empirical Bayes estimates of random effects in linear mixed models, except that in the latter case, where weights depend on unknown values of components of variance, these unknown variances are replaced by sample-based estimates.
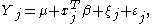
where ξj and εj represent the random effect and observation error for observation j, and suppose they are uncorrelated and have known variances σξ2 and σε2, respectively. Further, xj is a vector of independent variables
for the jth observation and β is a vector of regression parameters. The BLUP problem of providing an estimate of the observation-error-free value for the kth observation,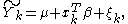
can be formulated as requiring that the coefficients of a linear predictor, defined as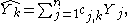
should be chosen so as to minimise the variance of the prediction error,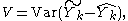
subject to the condition that the predictor is unbiased,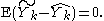
In contrast to the case of best linear unbiased estimation, the "quantity to be estimated",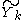
, not only has a contribution from a random element but one of the observed quantities, specifically 
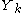which contributes to 
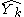, also has a contribution from this same random element.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, best linear unbiased prediction (BLUP) is used in linear mixed model
Mixed model
A mixed model is a statistical model containing both fixed effects and random effects, that is mixed effects. These models are useful in a wide variety of disciplines in the physical, biological and social sciences....
s for the estimation of random effects. BLUP was derived by Charles Roy Henderson
Charles Roy Henderson
Charles Roy Henderson was a statistician and a pioneer in animal breeding — the application of quantitative methods for the genetic evaluation of domestic livestock. He developed mixed model equations to obtain best linear unbiased predictions of breeding values and, in general, any random effect...
in 1950 but the term "best linear unbiased predictor" (or "prediction") seems not to have been used until 1962. "Best linear unbiased predictions" (BLUPs) of random effects are similar to best linear unbiased estimates (BLUEs) (see Gauss–Markov theorem
Gauss–Markov theorem
In statistics, the Gauss–Markov theorem, named after Carl Friedrich Gauss and Andrey Markov, states that in a linear regression model in which the errors have expectation zero and are uncorrelated and have equal variances, the best linear unbiased estimator of the coefficients is given by the...
) of fixed effects. The distinction arises because it is conventional to talk about estimating fixed effects but predicting random effects, but the two terms are otherwise equivalent. (This is a bit strange since the random effects have already been "realized" − they already exist. The use of the term "prediction" may be because in the field of animal breeding in which Henderson worked, the random effects were usually genetic merit, which could be used to predict the quality of offspring. (Robinson page 28)) However, the equations for the "fixed" effects and for the random effects are different.
In practice, it is often the case that the parameters associated with the random effect(s) term(s) are unknown; these parameters are the variances of the random effects and residuals. Typically the parameters are estimated and plugged into the predictor, leading to the Empirical Best Linear Unbiased Predictor (EBLUP). Notice that by simply plugging in the estimated parameter into the predictor, additional variability is unaccounted for, leading to overly optimistic prediction variances for the EBLUP.
Best linear unbiased predictions are similar to empirical Bayes estimates of random effects in linear mixed models, except that in the latter case, where weights depend on unknown values of components of variance, these unknown variances are replaced by sample-based estimates.
Example
Suppose that the model for observations {Yj; j=1,...,n} is written as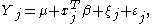where ξj and εj represent the random effect and observation error for observation j, and suppose they are uncorrelated and have known variances σξ2 and σε2, respectively. Further, xj is a vector of independent variables
Dependent and independent variables
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
for the jth observation and β is a vector of regression parameters. The BLUP problem of providing an estimate of the observation-error-free value for the kth observation,
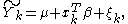
can be formulated as requiring that the coefficients of a linear predictor, defined as
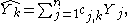
should be chosen so as to minimise the variance of the prediction error,
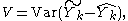
subject to the condition that the predictor is unbiased,
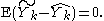
In contrast to the case of best linear unbiased estimation, the "quantity to be estimated",
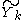, not only has a contribution from a random element but one of the observed quantities, specifically 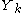which contributes to 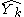, also has a contribution from this same random element.