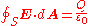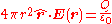Gauss's law
Encyclopedia
In physics
, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge
to the resulting electric field
. Gauss's law states that:
The electric flux through any closed surface is proportional to the enclosed electric charge
.
The law was formulated by Carl Friedrich Gauss
in 1835, but was not published until 1867. It is one of the four Maxwell's equations
which form the basis of classical electrodynamics, the other three being Gauss's law for magnetism, Faraday's law of induction
, and Ampère's law with Maxwell's correction. Gauss's law can be used to derive Coulomb's law
, and vice versa.
Gauss's law may be expressed as: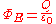
where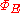 is the electric flux through a closed surface S, Q is the total charge
is the electric flux through a closed surface S, Q is the total charge
enclosed within S, and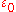 is the electric constant
is the electric constant
. The electric flux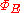 is defined as a surface integral
is defined as a surface integral
of the electric field
: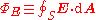
Because the flux is defined as an integral of the electric field, this expression of Gauss's law is called the integral form.
Gauss's law can alternatively be written in the differential form: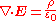
where ∇ · E is the divergence
of the electric field
, and ρ is the charge density
.
The integral and differential forms are related by the divergence theorem
, also called Gauss's theorem. Each of these forms can also be expressed two ways: In terms of a relation between the electric field E and the total electric charge, or in terms of the electric displacement field D and the free electric charge.
Gauss's law has a close mathematical similarity with a number of laws in other areas of physics, such as Gauss's law for magnetism and Gauss's law for gravity. In fact, any "inverse-square law
" can be formulated in a way similar to Gauss's law: For example, Gauss's law itself is essentially equivalent to the inverse-square Coulomb's law
, and Gauss's law for gravity is essentially equivalent to the inverse-square Newton's law of gravity.
Gauss's law can be used to demonstrate that all electric fields inside a Faraday cage
have an electric charge. Gauss's law is something of an electrical analogue of Ampère's law
, which deals with magnetism.
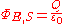
where ΦE,S is the electric flux through S, Q is total charge inside V, and ε0 is the electric constant
. The electric flux is given by a surface integral
over a closed surface S: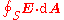
where E is the electric field, dA is a vector representing an infinitesimal
element of area
, and · represents the dot product
.
However, much more often, it is the reverse problem that needs to be solved: The electric charge distribution is known, and the electric field needs to be computed. This is much more difficult, since if you know the total flux through a given surface, that gives almost no information about the electric field, which (for all you know) could go in and out of the surface in arbitrarily complicated patterns.
An exception is if there is some symmetry
in the situation, which mandates that the electric field passes through the surface in a uniform way. Then, if the total flux is known, the field itself can be deduced at every point. Common examples of symmetries which lend themselves to Gauss's law include cylindrical symmetry, planar symmetry, and spherical symmetry. See the article Gaussian surface
for examples where these symmetries are exploited to compute electric fields.
, Gauss's law states:
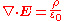
where ∇ · denotes divergence
, E is the electric field, and ρ is the total electric charge density
(including both free and bound charge), and ε0 is the electric constant. This is mathematically equivalent to the integral form, because of the divergence theorem
.
. Here is the argument more specifically:
The integral form of Gauss's law is: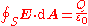
for any closed surface S containing charge Q. By the divergence theorem, this equation is equivalent to: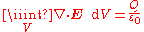
for any volume V containing charge Q. By the relation between charge and charge density, this equation is equivalent to: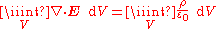
for any volume V. In order for this equation to be simultaneously true for every possible volume V, it is necessary (and sufficient) for the integrands to be equal everywhere. Therefore, this equation is equivalent to: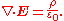
Thus the integral and differential forms are equivalent.
, or the charge on a capacitor
plate. In contrast, "bound charge" arises only in the context of dielectric
(polarizable) materials. (All materials are polarizable to some extent.) When such materials are placed in an external electric field, the electrons remain bound to their respective atoms, but shift a microscopic distance in response to the field, so that they're more on one side of the atom than the other. All these microscopic displacements add up to give a macroscopic net charge distribution, and this constitutes the "bound charge".
Although microscopically, all charge is fundamentally the same, there are often practical reasons for wanting to treat bound charge differently from free charge. The result is that the more "fundamental" Gauss's law, in terms of E, is sometimes put into the equivalent form below, which is in terms of D and the free charge only.

where ΦD,S is the flux of the electric displacement field D through S, and Qfree is the free charge contained in V. The flux ΦD,S is defined analogously to the flux ΦE,S of the electric field E through S. Specifically, it is given by the surface integral
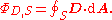

where ∇ · D is the divergence
of the electric displacement field, and ρfree is the free electric charge density.
The differential form and integral form are mathematically equivalent. The proof primarily involves the divergence theorem
.

where ε is the permittivity
of the material. Under these circumstances, there is yet another pair of equivalent formulations of Gauss's law:
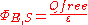
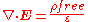
, which states that the electric field due to a stationary point charge is:
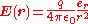
where
Using the expression from Coulomb's law, we get the total field at r by using an integral to sum the field at r due to the infinitesimal charge at each other point s in space, to give
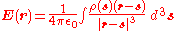
where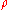 is the charge density. If we take the divergence of both sides of this equation with respect to r, and use the known theorem
is the charge density. If we take the divergence of both sides of this equation with respect to r, and use the known theorem
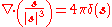
where δ(s) is the Dirac delta function
, the result is
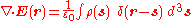
Using the "sifting property" of the Dirac delta function, we arrive at

which is the differential form of Gauss's law, as desired.
Note that since Coulomb's law only applies to stationary charges, there is no reason to expect Gauss's law to hold for moving charges based on this derivation alone. In fact, Gauss's law does hold for moving charges, and in this respect Gauss's law is more general than Coulomb's law.
and Faraday's law
). However, Coulomb's law can be proven from Gauss's law if it is assumed, in addition, that the electric field from a point charge is spherically-symmetric (this assumption, like Coulomb's law itself, is exactly true if the charge is stationary, and approximately true if the charge is in motion).
Taking S in the integral form of Gauss's law to be a spherical surface of radius r, centered at the point charge Q, we have
By the assumption of spherical symmetry, the integrand is a constant which can be taken out of the integral. The result is
where is a unit vector pointing radially away from the charge. Again by spherical symmetry, E points in the radial direction, and so we get
is a unit vector pointing radially away from the charge. Again by spherical symmetry, E points in the radial direction, and so we get
which is essentially equivalent to Coulomb's law. Thus the inverse-square law
dependence of the electric field in Coulomb's law follows from Gauss's law.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
to the resulting electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
. Gauss's law states that:
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
.
The law was formulated by Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
in 1835, but was not published until 1867. It is one of the four Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
which form the basis of classical electrodynamics, the other three being Gauss's law for magnetism, Faraday's law of induction
Faraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
, and Ampère's law with Maxwell's correction. Gauss's law can be used to derive Coulomb's law
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
, and vice versa.
Gauss's law may be expressed as:
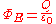
where
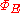 is the electric flux through a closed surface S, Q is the total charge
is the electric flux through a closed surface S, Q is the total chargeElectric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
enclosed within S, and
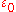 is the electric constant
is the electric constantElectric constant
The physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum...
. The electric flux
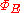 is defined as a surface integral
is defined as a surface integralSurface integral
In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
of the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
:
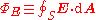
Because the flux is defined as an integral of the electric field, this expression of Gauss's law is called the integral form.
Gauss's law can alternatively be written in the differential form:
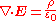
where ∇ · E is the divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
, and ρ is the charge density
Charge density
The linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as...
.
The integral and differential forms are related by the divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
, also called Gauss's theorem. Each of these forms can also be expressed two ways: In terms of a relation between the electric field E and the total electric charge, or in terms of the electric displacement field D and the free electric charge.
Gauss's law has a close mathematical similarity with a number of laws in other areas of physics, such as Gauss's law for magnetism and Gauss's law for gravity. In fact, any "inverse-square law
Inverse-square law
In physics, an inverse-square law is any physical law stating that a specified physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity....
" can be formulated in a way similar to Gauss's law: For example, Gauss's law itself is essentially equivalent to the inverse-square Coulomb's law
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
, and Gauss's law for gravity is essentially equivalent to the inverse-square Newton's law of gravity.
Gauss's law can be used to demonstrate that all electric fields inside a Faraday cage
Faraday cage
A Faraday cage or Faraday shield is an enclosure formed by conducting material or by a mesh of such material. Such an enclosure blocks out external static and non-static electric fields...
have an electric charge. Gauss's law is something of an electrical analogue of Ampère's law
Ampère's law
In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
, which deals with magnetism.
Integral form
For a volume V with surface S, Gauss's law states that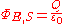
where ΦE,S is the electric flux through S, Q is total charge inside V, and ε0 is the electric constant
Electric constant
The physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum...
. The electric flux is given by a surface integral
Surface integral
In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
over a closed surface S:
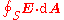
where E is the electric field, dA is a vector representing an infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
element of area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
, and · represents the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
.
Applying the integral form
If the electric field is known everywhere, Gauss's law makes it quite easy, in principle, to find the distribution of electric charge: The charge in any given region can be deduced by integrating the electric field to find the flux.However, much more often, it is the reverse problem that needs to be solved: The electric charge distribution is known, and the electric field needs to be computed. This is much more difficult, since if you know the total flux through a given surface, that gives almost no information about the electric field, which (for all you know) could go in and out of the surface in arbitrarily complicated patterns.
An exception is if there is some symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
in the situation, which mandates that the electric field passes through the surface in a uniform way. Then, if the total flux is known, the field itself can be deduced at every point. Common examples of symmetries which lend themselves to Gauss's law include cylindrical symmetry, planar symmetry, and spherical symmetry. See the article Gaussian surface
Gaussian surface
A Gaussian surface is a closed surface in three dimensional space through which the flux of an electromagnetic field is calculated. It is an arbitrary closed surface S=\partial V used in conjunction with Gauss's law in order to calculate the total enclosed electric charge by performing a surface...
for examples where these symmetries are exploited to compute electric fields.
Differential form
In differential formPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
, Gauss's law states:
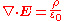
where ∇ · denotes divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
, E is the electric field, and ρ is the total electric charge density
Charge density
The linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as...
(including both free and bound charge), and ε0 is the electric constant. This is mathematically equivalent to the integral form, because of the divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
.
Equivalence of integral and differential forms
The integral and differential forms are mathematically equivalent, by the divergence theoremDivergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
. Here is the argument more specifically:
The integral form of Gauss's law is:
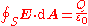
for any closed surface S containing charge Q. By the divergence theorem, this equation is equivalent to:
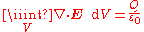
for any volume V containing charge Q. By the relation between charge and charge density, this equation is equivalent to:
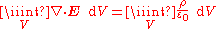
for any volume V. In order for this equation to be simultaneously true for every possible volume V, it is necessary (and sufficient) for the integrands to be equal everywhere. Therefore, this equation is equivalent to:
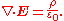
Thus the integral and differential forms are equivalent.
Free versus bound charge
The electric charge that arises in the simplest textbook situations would be classified as "free charge"—for example, the charge which is transferred in static electricityStatic electricity
Static electricity refers to the build-up of electric charge on the surface of objects. The static charges remain on an object until they either bleed off to ground or are quickly neutralized by a discharge. Static electricity can be contrasted with current electricity, which can be delivered...
, or the charge on a capacitor
Capacitor
A capacitor is a passive two-terminal electrical component used to store energy in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors separated by a dielectric ; for example, one common construction consists of metal foils separated...
plate. In contrast, "bound charge" arises only in the context of dielectric
Dielectric
A dielectric is an electrical insulator that can be polarized by an applied electric field. When a dielectric is placed in an electric field, electric charges do not flow through the material, as in a conductor, but only slightly shift from their average equilibrium positions causing dielectric...
(polarizable) materials. (All materials are polarizable to some extent.) When such materials are placed in an external electric field, the electrons remain bound to their respective atoms, but shift a microscopic distance in response to the field, so that they're more on one side of the atom than the other. All these microscopic displacements add up to give a macroscopic net charge distribution, and this constitutes the "bound charge".
Although microscopically, all charge is fundamentally the same, there are often practical reasons for wanting to treat bound charge differently from free charge. The result is that the more "fundamental" Gauss's law, in terms of E, is sometimes put into the equivalent form below, which is in terms of D and the free charge only.
Integral form
This formulation of Gauss's law states that, for any volume V in space, with surface S, the following equation holds:
where ΦD,S is the flux of the electric displacement field D through S, and Qfree is the free charge contained in V. The flux ΦD,S is defined analogously to the flux ΦE,S of the electric field E through S. Specifically, it is given by the surface integral
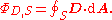
Differential form
The differential form of Gauss's law, involving free charge only, states:
where ∇ · D is the divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of the electric displacement field, and ρfree is the free electric charge density.
The differential form and integral form are mathematically equivalent. The proof primarily involves the divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
.
Equivalence of total and free charge statements
| Proof that the formulations of Gauss's law in terms of free charge are equivalent to the formulations involving total charge. |
|---|
In this proof, we will show that the equation is equivalent to the equation 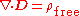 Note that we're only dealing with the differential forms, not the integral forms, but that is sufficient since the differential and integral forms are equivalent in each case, by the divergence theorem. We introduce the polarization density Polarization density In classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is... P, which has the following relation to E and D:  and the following relation to the bound charge:  Now, consider the three equations: 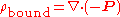  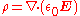 The key insight is that the sum of the first two equations is the third equation. This completes the proof: The first equation is true by definition, and therefore the second equation is true if and only if If and only if In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements.... the third equation is true. So the second and third equations are equivalent, which is what we wanted to prove. |
In linear materials
In homogeneous, isotropic, nondispersive, linear materials, there is a nice, simple relationship between E and D:
where ε is the permittivity
Permittivity
In electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
of the material. Under these circumstances, there is yet another pair of equivalent formulations of Gauss's law:
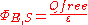
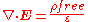
Deriving Gauss's law from Coulomb's law
Gauss's law can be derived from Coulomb's lawCoulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
, which states that the electric field due to a stationary point charge is:
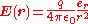
where
- er is the radial unit vector,
- r is the radius, |r|,
 is the electric constantElectric constantThe physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum...
is the electric constantElectric constantThe physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum...
, - q is the charge of the particle, which is assumed to be located at the originOrigin (mathematics)In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
.
Using the expression from Coulomb's law, we get the total field at r by using an integral to sum the field at r due to the infinitesimal charge at each other point s in space, to give
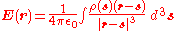
where
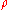 is the charge density. If we take the divergence of both sides of this equation with respect to r, and use the known theorem
is the charge density. If we take the divergence of both sides of this equation with respect to r, and use the known theorem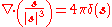
where δ(s) is the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
, the result is
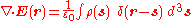
Using the "sifting property" of the Dirac delta function, we arrive at

which is the differential form of Gauss's law, as desired.
Note that since Coulomb's law only applies to stationary charges, there is no reason to expect Gauss's law to hold for moving charges based on this derivation alone. In fact, Gauss's law does hold for moving charges, and in this respect Gauss's law is more general than Coulomb's law.
Deriving Coulomb's law from Gauss's law
Strictly speaking, Coulomb's law cannot be derived from Gauss's law alone, since Gauss's law does not give any information regarding the curl of E (see Helmholtz decompositionHelmholtz decomposition
In physics and mathematics, in the area of vector calculus, Helmholtz's theorem, also known as the fundamental theorem of vector calculus, states that any sufficiently smooth, rapidly decaying vector field in three dimensions can be resolved into the sum of an irrotational vector field and a...
and Faraday's law
Faraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
). However, Coulomb's law can be proven from Gauss's law if it is assumed, in addition, that the electric field from a point charge is spherically-symmetric (this assumption, like Coulomb's law itself, is exactly true if the charge is stationary, and approximately true if the charge is in motion).
Taking S in the integral form of Gauss's law to be a spherical surface of radius r, centered at the point charge Q, we have
By the assumption of spherical symmetry, the integrand is a constant which can be taken out of the integral. The result is
where
 is a unit vector pointing radially away from the charge. Again by spherical symmetry, E points in the radial direction, and so we get
is a unit vector pointing radially away from the charge. Again by spherical symmetry, E points in the radial direction, and so we getwhich is essentially equivalent to Coulomb's law. Thus the inverse-square law
Inverse-square law
In physics, an inverse-square law is any physical law stating that a specified physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity....
dependence of the electric field in Coulomb's law follows from Gauss's law.
See also
- Method of image chargesMethod of image chargesThe method of image charges is a basic problem-solving tool in electrostatics...
- Uniqueness theorem for Poisson's equation
External links
- MIT Video Lecture Series (30 x 50 minute lectures)- Electricity and Magnetism Taught by Professor Walter LewinWalter LewinWalter H. G. Lewin is a professor emeritus of physics at the Massachusetts Institute of Technology .-Education and career:...
. - section on Gauss's law in an online textbook
- MISN-0-132 Gauss's Law for Spherical Symmetry (PDF filePortable Document FormatPortable Document Format is an open standard for document exchange. This file format, created by Adobe Systems in 1993, is used for representing documents in a manner independent of application software, hardware, and operating systems....
) by Peter Signell for Project PHYSNET. - MISN-0-133 Gauss's Law Applied to Cylindrical and Planar Charge Distributions (PDF file) by Peter Signell for Project PHYSNET.