Gamma process
Encyclopedia
A gamma process is a random process with independent
gamma distributed increments. Often written as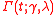
, it is a pure-jump increasing Lévy process
with intensity measure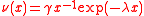
, for positive 
. Thus jumps whose size lies in the interval 
occur as a Poisson process
with intensity
.The parameter 
controls the rate of jump arrivals and the scaling parameter 
inversely controls the jump size.
The marginal distribution
of a gamma process at time
, is a gamma distribution with mean 
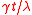and variance 
.
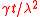The gamma process is sometimes also parameterised in terms of the mean (
) and variance (
) per unit time, which is equivalent to 
and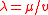 
.
Some basic properties of the gamma process are:
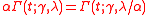(scaling)
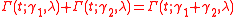(adding independent processes)
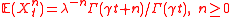(moments), where 
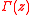is the Gamma function
.
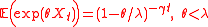(moment generating function)
, for any gamma process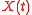 
The gamma process is used as the distribution for random time change in the variance gamma process
.
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
gamma distributed increments. Often written as
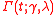, it is a pure-jump increasing Lévy processLévy process
In probability theory, a Lévy process, named after the French mathematician Paul Lévy, is any continuous-time stochastic process that starts at 0, admits càdlàg modification and has "stationary independent increments" — this phrase will be explained below...
with intensity measure
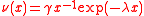, for positive . Thus jumps whose size lies in the interval occur as a Poisson processPoisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
with intensity
.The parameter controls the rate of jump arrivals and the scaling parameter inversely controls the jump size.The marginal distribution
Marginal distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained...
of a gamma process at time
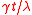, is a gamma distribution with mean and variance 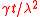.The gamma process is sometimes also parameterised in terms of the mean (
) and variance () per unit time, which is equivalent to and 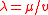.Some basic properties of the gamma process are:
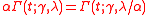(scaling) 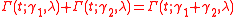(adding independent processes) 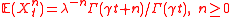(moments), where 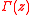is the Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
.
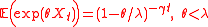(moment generating function), for any gamma process 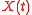The gamma process is used as the distribution for random time change in the variance gamma process
Variance gamma process
In the theory of stochastic processes, a part of the mathematical theory of probability, the variance gamma process , also known as Laplace motion, is a Lévy process determined by a random time change. The process has finite moments distinguishing it from many Lévy processes. There is no diffusion...
.