
Frobenius manifold
Encyclopedia
In the mathematical field of differential geometry, a Frobenius manifold is a flat Riemannian manifold
with a certain compatible multiplicative structure on the tangent space
. The concept generalizes the notion of Frobenius algebra
to tangent bundles. They were introduced by Dubrovin.
Frobenius manifolds occur naturally in the subject of symplectic topology
, more specifically quantum cohomology
. The broadest definition is in the category of Riemannian supermanifold
s. We will limit the discussion here to smooth (real) manifolds. A restriction to complex manifolds is also possible.
Tf of vector spaces that pointwisely span TM the tangent bundle and the tangent bracket of pairs of its sections vanishes.
As a local example consider the coordinate vectorfields over a chart of M. A manifold admits an affine flat structure if one can glue together such vectorfields for a covering family of charts.
Let further be given a Riemannian metric g on M. It is compatible to the flat structure if g(X, Y) is locally constant for all flat vector fields X and Y.
A Riemannian manifold admits a compatible affine flat structure if and only if its curvature tensor
vanishes everywhere.
A family of commutative products * on TM is equivalent to a section A of S2(T*M) ⊗ TM via

We require in addition the property

Therefore the composition g#∘A is a symmetric 3-tensor.
This implies in particular that a linear Frobenius manifold (M, g, *) with constant product is a Frobenius algebra M.
Given (g, Tf, A), a local potential Φ is a local smooth function such that
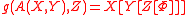
for all flat vector fields X, Y, and Z.
A Frobenius manifold (M, g, *) is now a flat Riemannian manifold (M, g) with symmetric 3-tensor A that admits everywhere a local potential and is associative.
in the local potential Φ
where Einstein's sum convention is implied, Φ,a denotes the partial derivative of the function Φ by the coordinate vectorfield ∂/∂xa which are all assumed to be flat. gef are the coefficients of the inverse of the metric.
The equation is therefore called associativity equation or Witten–Dijkgraaf–Verlinde–Verlinde (WDVV) equation.
(M, ω) then there exists an open neighborhood U of 0 in its even quantum cohomology
QHeven(M, ω) with Novikov ring over C such that the big quantum product *a for a in U is analytic. Now U together with the intersection form
g = <·,·> is a (complex) Frobenius manifold.
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
with a certain compatible multiplicative structure on the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
. The concept generalizes the notion of Frobenius algebra
Frobenius algebra
In mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in...
to tangent bundles. They were introduced by Dubrovin.
Frobenius manifolds occur naturally in the subject of symplectic topology
Symplectic topology
Symplectic geometry is a branch of differential geometry and differential topology which studies symplectic manifolds; that is, differentiable manifolds equipped with a closed, nondegenerate 2-form...
, more specifically quantum cohomology
Quantum cohomology
In mathematics, specifically in symplectic topology and algebraic geometry, a quantum cohomology ring is an extension of the ordinary cohomology ring of a closed symplectic manifold. It comes in two versions, called small and big; in general, the latter is more complicated and contains more...
. The broadest definition is in the category of Riemannian supermanifold
Supermanifold
In physics and mathematics, supermanifolds are generalizations of the manifold concept based on ideas coming from supersymmetry. Several definitions are in use, some of which are described below.- Physics :...
s. We will limit the discussion here to smooth (real) manifolds. A restriction to complex manifolds is also possible.
Definition
Let M be a smooth manifold. An affine flat structure on M is a sheafSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
Tf of vector spaces that pointwisely span TM the tangent bundle and the tangent bracket of pairs of its sections vanishes.
As a local example consider the coordinate vectorfields over a chart of M. A manifold admits an affine flat structure if one can glue together such vectorfields for a covering family of charts.
Let further be given a Riemannian metric g on M. It is compatible to the flat structure if g(X, Y) is locally constant for all flat vector fields X and Y.
A Riemannian manifold admits a compatible affine flat structure if and only if its curvature tensor
Curvature tensor
In differential geometry, the term curvature tensor may refer to:* the Riemann curvature tensor of a Riemannian manifold — see also Curvature of Riemannian manifolds;* the curvature of an affine connection or covariant derivative ;...
vanishes everywhere.
A family of commutative products * on TM is equivalent to a section A of S2(T*M) ⊗ TM via

We require in addition the property

Therefore the composition g#∘A is a symmetric 3-tensor.
This implies in particular that a linear Frobenius manifold (M, g, *) with constant product is a Frobenius algebra M.
Given (g, Tf, A), a local potential Φ is a local smooth function such that
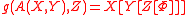
for all flat vector fields X, Y, and Z.
A Frobenius manifold (M, g, *) is now a flat Riemannian manifold (M, g) with symmetric 3-tensor A that admits everywhere a local potential and is associative.
Elementary properties
The associativity of the product * is equivalent to the following quadratic PDEPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
in the local potential Φ

where Einstein's sum convention is implied, Φ,a denotes the partial derivative of the function Φ by the coordinate vectorfield ∂/∂xa which are all assumed to be flat. gef are the coefficients of the inverse of the metric.
The equation is therefore called associativity equation or Witten–Dijkgraaf–Verlinde–Verlinde (WDVV) equation.
Examples
Beside Frobenius algebras, examples arise from quantum cohomology. Namely, given a semipositive symplectic manifoldSymplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
(M, ω) then there exists an open neighborhood U of 0 in its even quantum cohomology
Quantum cohomology
In mathematics, specifically in symplectic topology and algebraic geometry, a quantum cohomology ring is an extension of the ordinary cohomology ring of a closed symplectic manifold. It comes in two versions, called small and big; in general, the latter is more complicated and contains more...
QHeven(M, ω) with Novikov ring over C such that the big quantum product *a for a in U is analytic. Now U together with the intersection form
Intersection form
Intersection form may refer to:*Intersection theory *intersection form...
g = <·,·> is a (complex) Frobenius manifold.

