Free Boolean algebra
Encyclopedia
In abstract algebra
, a branch of mathematics
, a free Boolean algebra is a Boolean algebra 〈B,F〉, such that the set B (called the carrier) has a subset
whose elements are called generators
. The generators satisfy the following properties:
of a free Boolean algebra can represent independent proposition
s. Consider, for example, the propositions "John is tall" and "Mary is rich". These generate a Boolean algebra with four atoms
, namely:
Other elements of the Boolean algebra are then logical disjunction
s of the atoms, such as "John is tall and Mary is not rich, or John is not tall and Mary is rich". In addition there is one more element, FALSE, which can be thought of as the empty disjunction; that is, the disjunction of no atoms.
This example yields a Boolean algebra with 16 elements; in general, for finite n, the free Boolean algebra with n generators has 2n atoms
, and therefore
elements.
If there are infinitely many generators
, a similar situation prevails except that now there are no atoms
. Each element of the Boolean algebra is a combination of finitely many of the generating propositions, with two such elements deemed identical if they are logically equivalent
.
, free Boolean algebras can be defined simply in terms of an adjunction between the category of sets and functions, Set, and the category of Boolean algebras and Boolean algebra homomorphisms, BA. In fact, this approach generalizes to any algebraic structure definable in the framework of universal algebra
.
Above, we said that a free Boolean algebra is a Boolean algebra with a set of generators that behave a certain way; alternatively, one might start with a set and ask which algebra it generates. Every set X generates a free Boolean algebra FX defined as the algebra such that for every algebra B and function f : X → B, there is a unique Boolean algebra homomorphism f′ : FX → B that extends f. Diagrammatically
,
where iX is the inclusion, and the dashed arrow denotes uniqueness. The idea is that once one chooses where to send the elements of X, the laws for Boolean algebra homomorphisms determine where to send everything else in the free algebra FX. If FX contained elements inexpressible as combinations of elements of X, then f′ wouldn't be unique, and if the elements of FX weren't sufficiently independent, then f′ wouldn't be well defined! It's easily shown that FX is unique (up to isomorphism), so this definition makes sense. It's also easily shown that a free Boolean algebra with generating set X, as defined originally, is isomorphic to FX, so the two definitions agree.
One shortcoming of the above definition is that the diagram doesn't capture that f′ is a homomorphism; since it's a diagram in Set each arrow denotes a mere function. We can fix this by separating it into two diagrams, one in BA and one in Set. To relate the two, we introduce a functor
U : BA → Set that "forgets
" the algebraic structure, mapping algebras and homomorphisms to their underlying sets and functions.
If we interpret the top arrow as a diagram in BA and the bottom triangle as a diagram in Set, then this diagram properly expresses that every function f : X → B extends to a unique Boolean algebra homomorphism f′ : FX → B. The functor U can be thought of as a device to pull the homomorphism f′ back into Set so it can be related to f.
The remarkable aspect of this is that the latter diagram is one of the various (equivalent) definitions of when two functors are adjoint
. Our F easily extends to a functor Set → BA, and our definition of X generating a free Boolean algebra FX is precisely that U has a left adjoint F.
, where κ is a finite or infinite cardinal number
, may be realized as the collection of all clopen
subset
s of {0,1}κ, given the product topology
assuming that {0,1} has the discrete topology. For each α<κ, the αth generator is the set of all elements of {0,1}κ whose αth coordinate is 1. In particular, the free Boolean algebra with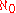
generators is the collection of all clopen subsets
of a Cantor space
. Surprisingly, this collection is countable
. In fact, while the free Boolean algebra with n generators, n finite, has cardinality
, the free Boolean algebra with 
generators has cardinality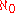 
.
For more on this topological
approach to free Boolean algebra, see Stone's representation theorem for Boolean algebras
.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a free Boolean algebra is a Boolean algebra 〈B,F〉, such that the set B (called the carrier) has a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
whose elements are called generators
Generating set
In mathematics, the expressions generator, generate, generated by and generating set can have several closely related technical meanings:...
. The generators satisfy the following properties:
- Each element of B that is not a generator can be expressed as a finite combination of generatorsGenerating setIn mathematics, the expressions generator, generate, generated by and generating set can have several closely related technical meanings:...
, using the elements of F, which are operationsOperation (mathematics)The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
; - The generators are as "independent" as possible, in that any equation holding for finite termsTerm (mathematics)A term is a mathematical expression which may form a separable part of an equation, a series, or another expression.-Definition:In elementary mathematics, a term is either a single number or variable, or the product of several numbers or variables separated from another term by a + or - sign in an...
formed from the generators using the operations in F, also holds for all elements of all possible Boolean algebras.
A simple example
The generatorsGenerating set
In mathematics, the expressions generator, generate, generated by and generating set can have several closely related technical meanings:...
of a free Boolean algebra can represent independent proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
s. Consider, for example, the propositions "John is tall" and "Mary is rich". These generate a Boolean algebra with four atoms
Atomic (order theory)
In the mathematical field of order theory, given two elements a and b of a partially ordered set, one says that b covers a, and writes a a, if a ...
, namely:
- John is tall, and Mary is rich;
- John is tall, and Mary is not rich;
- John is not tall, and Mary is rich;
- John is not tall, and Mary is not rich.
Other elements of the Boolean algebra are then logical disjunction
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
s of the atoms, such as "John is tall and Mary is not rich, or John is not tall and Mary is rich". In addition there is one more element, FALSE, which can be thought of as the empty disjunction; that is, the disjunction of no atoms.
This example yields a Boolean algebra with 16 elements; in general, for finite n, the free Boolean algebra with n generators has 2n atoms
Atomic (order theory)
In the mathematical field of order theory, given two elements a and b of a partially ordered set, one says that b covers a, and writes a a, if a ...
, and therefore
elements.If there are infinitely many generators
Generating set
In mathematics, the expressions generator, generate, generated by and generating set can have several closely related technical meanings:...
, a similar situation prevails except that now there are no atoms
Atomic (order theory)
In the mathematical field of order theory, given two elements a and b of a partially ordered set, one says that b covers a, and writes a a, if a ...
. Each element of the Boolean algebra is a combination of finitely many of the generating propositions, with two such elements deemed identical if they are logically equivalent
Logical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
.
Category-theoretic definition
In the language of category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, free Boolean algebras can be defined simply in terms of an adjunction between the category of sets and functions, Set, and the category of Boolean algebras and Boolean algebra homomorphisms, BA. In fact, this approach generalizes to any algebraic structure definable in the framework of universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
.
Above, we said that a free Boolean algebra is a Boolean algebra with a set of generators that behave a certain way; alternatively, one might start with a set and ask which algebra it generates. Every set X generates a free Boolean algebra FX defined as the algebra such that for every algebra B and function f : X → B, there is a unique Boolean algebra homomorphism f′ : FX → B that extends f. Diagrammatically
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
,
where iX is the inclusion, and the dashed arrow denotes uniqueness. The idea is that once one chooses where to send the elements of X, the laws for Boolean algebra homomorphisms determine where to send everything else in the free algebra FX. If FX contained elements inexpressible as combinations of elements of X, then f′ wouldn't be unique, and if the elements of FX weren't sufficiently independent, then f′ wouldn't be well defined! It's easily shown that FX is unique (up to isomorphism), so this definition makes sense. It's also easily shown that a free Boolean algebra with generating set X, as defined originally, is isomorphic to FX, so the two definitions agree.
One shortcoming of the above definition is that the diagram doesn't capture that f′ is a homomorphism; since it's a diagram in Set each arrow denotes a mere function. We can fix this by separating it into two diagrams, one in BA and one in Set. To relate the two, we introduce a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
U : BA → Set that "forgets
Forgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
" the algebraic structure, mapping algebras and homomorphisms to their underlying sets and functions.
If we interpret the top arrow as a diagram in BA and the bottom triangle as a diagram in Set, then this diagram properly expresses that every function f : X → B extends to a unique Boolean algebra homomorphism f′ : FX → B. The functor U can be thought of as a device to pull the homomorphism f′ back into Set so it can be related to f.
The remarkable aspect of this is that the latter diagram is one of the various (equivalent) definitions of when two functors are adjoint
Adjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
. Our F easily extends to a functor Set → BA, and our definition of X generating a free Boolean algebra FX is precisely that U has a left adjoint F.
Topological realization
The free Boolean algebra with κ generatorsGenerating set
In mathematics, the expressions generator, generate, generated by and generating set can have several closely related technical meanings:...
, where κ is a finite or infinite cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
, may be realized as the collection of all clopen
Clopen set
In topology, a clopen set in a topological space is a set which is both open and closed. That this is possible for a set is not as counter-intuitive as it might seem if the terms open and closed were thought of as antonyms; in fact they are not...
subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of {0,1}κ, given the product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
assuming that {0,1} has the discrete topology. For each α<κ, the αth generator is the set of all elements of {0,1}κ whose αth coordinate is 1. In particular, the free Boolean algebra with
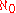generators is the collection of all clopen subsetsClopen set
In topology, a clopen set in a topological space is a set which is both open and closed. That this is possible for a set is not as counter-intuitive as it might seem if the terms open and closed were thought of as antonyms; in fact they are not...
of a Cantor space
Cantor space
In mathematics, a Cantor space, named for Georg Cantor, is a topological abstraction of the classical Cantor set: a topological space is a Cantor space if it is homeomorphic to the Cantor set. In set theory, the topological space 2ω is called "the" Cantor space...
. Surprisingly, this collection is countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
. In fact, while the free Boolean algebra with n generators, n finite, has cardinality
, the free Boolean algebra with generators has cardinality 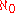.For more on this topological
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
approach to free Boolean algebra, see Stone's representation theorem for Boolean algebras
Stone's representation theorem for Boolean algebras
In mathematics, Stone's representation theorem for Boolean algebras states that every Boolean algebra is isomorphic to a field of sets. The theorem is fundamental to the deeper understanding of Boolean algebra that emerged in the first half of the 20th century. The theorem was first proved by Stone...
.