Fourier–Motzkin elimination
Encyclopedia
Fourier–Motzkin elimination, FME method, is a mathematical algorithm
for eliminating variables from a system of linear inequalities. It can look for both real
and integer
solutions. Its computational complexity is double-exponential.
Elimination (or ∃-elimination) of variables V from a system of relations (here, linear inequalities) consists in creating another system of the same kind, but without the variables V, such that both systems have the same solutions over the remaining variables.
If one eliminates all variables from a system of linear inequalities, then one obtains a system of constant inequalities, which can be trivially decided to be true or false, such that this system has solutions (is true) if and only if the original system has solutions. As a consequence, elimination of all variables can be used to detect whether a system of inequalities has solutions or not.
Let us consider a system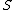
of 
inequalities with 
variables 
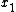to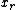 
, with 
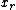the variable to eliminate. The linear inequalities in the system can be grouped into three classes, depending on the sign (positive, negative or null) of the coefficient for 
:
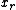The original system is thus equivalent to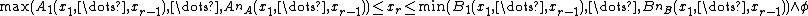
.
Elimination consists in producing a system equivalent to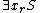
. Obviously, this formula is equivalent to 
.
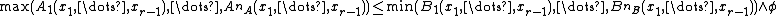The inequality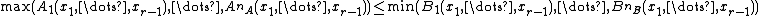
is equivalent to 
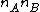inequalities 
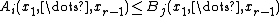, for 
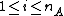and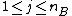 
.
We have therefore transformed the original system into another system where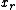
is eliminated. Note that the output system has 
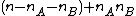inequalities. In particular, if 
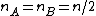, then the number of output inequalities is 
.
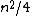The operation is named after Joseph Fourier
and Theodore Motzkin
.
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for eliminating variables from a system of linear inequalities. It can look for both real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
and integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
solutions. Its computational complexity is double-exponential.
Elimination (or ∃-elimination) of variables V from a system of relations (here, linear inequalities) consists in creating another system of the same kind, but without the variables V, such that both systems have the same solutions over the remaining variables.
If one eliminates all variables from a system of linear inequalities, then one obtains a system of constant inequalities, which can be trivially decided to be true or false, such that this system has solutions (is true) if and only if the original system has solutions. As a consequence, elimination of all variables can be used to detect whether a system of inequalities has solutions or not.
Let us consider a system
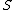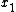of inequalities with variables to 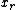, with 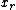the variable to eliminate. The linear inequalities in the system can be grouped into three classes, depending on the sign (positive, negative or null) of the coefficient for :
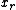- those that are equivalent to some inequalities of the form
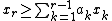; let us note these as 
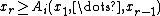, for 
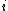ranging from 1 to 
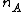where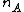 
is the number of such inequalities; - those that are equivalent to some inequalities of the form
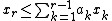; let us note these as 
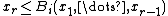, for 
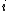ranging from 1 to 
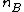where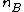 
is the number of such inequalities; - those in which
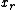plays no role, grouped into a single conjunction 
.
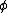The original system is thus equivalent to
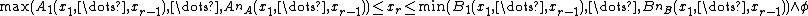.Elimination consists in producing a system equivalent to
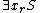. Obviously, this formula is equivalent to 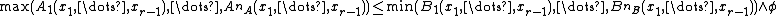.The inequality
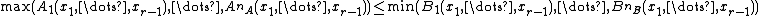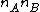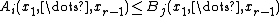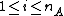is equivalent to inequalities , for and 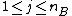.We have therefore transformed the original system into another system where
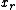is eliminated. Note that the output system has 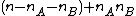inequalities. In particular, if 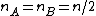, then the number of output inequalities is 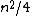.The operation is named after Joseph Fourier
Joseph Fourier
Jean Baptiste Joseph Fourier was a French mathematician and physicist best known for initiating the investigation of Fourier series and their applications to problems of heat transfer and vibrations. The Fourier transform and Fourier's Law are also named in his honour...
and Theodore Motzkin
Theodore Motzkin
Theodore Samuel Motzkin was an Israeli-American mathematician.- Biography :Motzkin's father, Leo Motzkin, was a noted Russian Zionist leader.Motzkin received his Ph.D...
.
See also
- Real closed fieldReal closed fieldIn mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
: the cylindrical algebraic decomposition algorithm performs quantifier elimination over polynomial inequalities, not just linear
External links
- Lectures on Convex Sets, notes by Niels Lauritzen, at Aarhus University, March 2010.