Force of mortality
Encyclopedia
In actuarial science
, force of mortality represents the instantaneous rate of mortality at a certain age measured on an annualized basis. It is identical in concept to failure rate
, also called hazard function, in reliability theory
.
, we consider the probability of a person dying from age x to x + 1, called qx. In the continuous case, we could also consider the conditional probability
of a person who has attained age (x) dying between ages x and x + Δx, which is
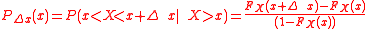
where FX(x) is the distribution function
of the continuous age-at-death random variable
, X. As Δx tends to zero, so does this probability in the continuous case. The approximate force of mortality is this probability divided by Δx. If we let Δx tend to zero, we get the function for force of mortality, denoted by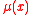
:
Since fX(x)=F 'X(x) is the probability density function of X, and S(x) = 1 - FX(x) is the survival function
, the force of mortality can also be expressed variously as:
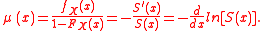
To understand conceptually how the force of mortality operates within a population, consider that the ages, x, where the probability density function fX(x) is zero, there is no chance of dying. Thus the force of mortality at these ages is zero.
The force of mortality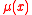
can be interpreted as the conditional density of failure at age x, while f(x) is the unconditional density of failure at age x. The unconditional density of failure at age x is the product of the probability of survival to age x, and the conditional density of failure at age x, given survival to age x.
This is expressed in symbols as
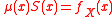
or equivalently
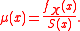
Actuarial science
Actuarial science is the discipline that applies mathematical and statistical methods to assess risk in the insurance and finance industries. Actuaries are professionals who are qualified in this field through education and experience...
, force of mortality represents the instantaneous rate of mortality at a certain age measured on an annualized basis. It is identical in concept to failure rate
Failure rate
Failure rate is the frequency with which an engineered system or component fails, expressed for example in failures per hour. It is often denoted by the Greek letter λ and is important in reliability engineering....
, also called hazard function, in reliability theory
Reliability theory
Reliability theory describes the probability of a system completing its expected function during an interval of time. It is the basis of reliability engineering, which is an area of study focused on optimizing the reliability, or probability of successful functioning, of systems, such as airplanes,...
.
Motivation and definition
In a life tableLife table
In actuarial science, a life table is a table which shows, for each age, what the probability is that a person of that age will die before his or her next birthday...
, we consider the probability of a person dying from age x to x + 1, called qx. In the continuous case, we could also consider the conditional probability
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
of a person who has attained age (x) dying between ages x and x + Δx, which is
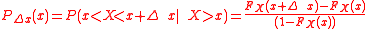
where FX(x) is the distribution function
Distribution function
In molecular kinetic theory in physics, a particle's distribution function is a function of seven variables, f, which gives the number of particles per unit volume in phase space. It is the number of particles per unit volume having approximately the velocity near the place and time...
of the continuous age-at-death random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
, X. As Δx tends to zero, so does this probability in the continuous case. The approximate force of mortality is this probability divided by Δx. If we let Δx tend to zero, we get the function for force of mortality, denoted by
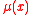:Since fX(x)=F 'X(x) is the probability density function of X, and S(x) = 1 - FX(x) is the survival function
Survival function
The survival function, also known as a survivor function or reliability function, is a property of any random variable that maps a set of events, usually associated with mortality or failure of some system, onto time. It captures the probability that the system will survive beyond a specified time...
, the force of mortality can also be expressed variously as:
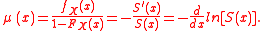
To understand conceptually how the force of mortality operates within a population, consider that the ages, x, where the probability density function fX(x) is zero, there is no chance of dying. Thus the force of mortality at these ages is zero.
The force of mortality
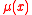can be interpreted as the conditional density of failure at age x, while f(x) is the unconditional density of failure at age x. The unconditional density of failure at age x is the product of the probability of survival to age x, and the conditional density of failure at age x, given survival to age x.This is expressed in symbols as
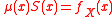
or equivalently
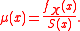
See also
- Failure rateFailure rateFailure rate is the frequency with which an engineered system or component fails, expressed for example in failures per hour. It is often denoted by the Greek letter λ and is important in reliability engineering....
- Hazard function
- Actuarial present valueActuarial present valueIn actuarial science, the actuarial present value of a payment or series of payments which are random variables is the expected value of the present value of the payments, or equivalently, the present value of their expected values....
- Actuarial scienceActuarial scienceActuarial science is the discipline that applies mathematical and statistical methods to assess risk in the insurance and finance industries. Actuaries are professionals who are qualified in this field through education and experience...
- Reliability theoryReliability theoryReliability theory describes the probability of a system completing its expected function during an interval of time. It is the basis of reliability engineering, which is an area of study focused on optimizing the reliability, or probability of successful functioning, of systems, such as airplanes,...