Fermi–Pasta–Ulam problem
Encyclopedia
In physics
, the Fermi–Pasta–Ulam problem or FPU problem was the apparent paradox in chaos theory
that many complicated enough physical systems exhibited almost exactly periodic
behavior instead of ergodic
behavior. One of the resolutions of the paradox includes the insight that many non-linear equations are exactly integrable. Another may be that ergodic behavior may depend on the initial energy of the system.
, Pasta
, Ulam
and Mary Tsingou conducted numerical experiments (i.e. computer simulations) of a vibrating string that included a non-linear term (quadratic in one test, cubic in another, and a piecewise linear approximation to a cubic in a third). They found that the behavior of the system was quite different from what intuition would have led them to expect. Fermi thought that after many iterations, the system would exhibit thermalization, an ergodic behavior in which the influence of the initial modes of vibration fade and the system becomes more or less random with all modes excited more or less equally
. Instead, the system exhibited a very complicated quasi-periodic behavior. They published their results in a Los Alamos technical report in 1955. (Note: Enrico Fermi
died in 1954 and so this technical report was published after Fermi's death.)
The FPU experiment was important both in showing the complexity of nonlinear system behavior and the value of computer simulation in analyzing systems.
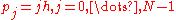where 
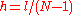is the lattice spacing. Then the position of the jth oscillator as a function of is 
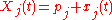so that 
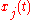gives the displacement from equilibrium. FPU used the following equations of motion:
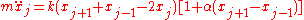
(Note: this equation is not equivalent to the classical one given in the French version of the article)
This is just Newton's second law
for the jth particle. The first factor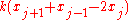
is just the usual Hooke's law
form for the force. The factor with
is the nonlinear force. We can rewrite this in terms of continuum quantities by defining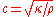 
to be the wave speed, where 
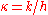is the Young's modulus
for the string and
is the density:
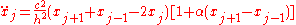
(KdV equation.) The discovery of this relationship and of the soliton
solutions of the KdV equation by Kruskal and Zabusky in 1965 was an important step forward in nonlinear system research. We reproduce below a derivation of this limit, which is rather tricky, as found in Palais's article. Beginning from the "continuum form" of the lattice equations above, we first define u(x,t) to be the displacement of the string at position x and time t. We'll then want a correspondence so that
is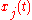 
.
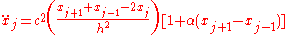
We can use Taylor's theorem
to rewrite the second factor for small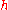
, (subscripts of u denote partial derivatives):
.
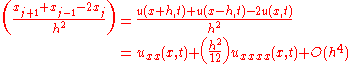Similarly, the second term in the third factor is:
.
Thus, the FPU system is:
.
If one were to keep terms up to O(h) only and assume that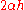
approaches a limit, the resulting equation is one which develops shocks
, which is not observed. Thus one keeps the O(h^2) term as well:
.
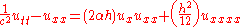We now make the following substitutions, motivated by the decomposition of traveling wave solutions (of the ordinary wave equation
, to which this reduces when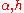
vanish) into left- and right-moving waves, so that we only consider a right-moving wave. Let 
. Under this change of coordinates, the equation becomes:
.
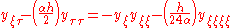To take the continuum limit, assume that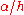
tends to a constant and 
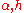tend to zero. If we take 
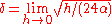, then:
.
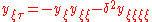Taking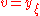
results in the KdV equation:
.
Zabusky and Kruskal argued that it was the fact that soliton solutions of the KdV equation can pass through one another without affecting the asymptotic shapes that explained the quasi-periodicity of the waves in the FPU experiment. In short, thermalization could not occur because of a certain "soliton symmetry" in the system which broke ergodicity.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the Fermi–Pasta–Ulam problem or FPU problem was the apparent paradox in chaos theory
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
that many complicated enough physical systems exhibited almost exactly periodic
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
behavior instead of ergodic
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
behavior. One of the resolutions of the paradox includes the insight that many non-linear equations are exactly integrable. Another may be that ergodic behavior may depend on the initial energy of the system.
The FPU experiment
In the Summer of 1953 FermiEnrico Fermi
Enrico Fermi was an Italian-born, naturalized American physicist particularly known for his work on the development of the first nuclear reactor, Chicago Pile-1, and for his contributions to the development of quantum theory, nuclear and particle physics, and statistical mechanics...
, Pasta
John Pasta
John R. Pasta was a computer scientist who is remembered today for the Fermi–Pasta–Ulam experiment, a result much discussed among physicists and researchers in dynamical systems and chaos theory, and as the head of the department of Computer Science at the University of Illinois at...
, Ulam
Stanislaw Marcin Ulam
Stanisław Marcin Ulam was a renowned mathematician of Polish-Jewish origin. He participated in America's Manhattan Project, originated the Teller–Ulam design of thermonuclear weapons, invented the Monte Carlo method of computation, and proposed the idea of nuclear pulse propulsion...
and Mary Tsingou conducted numerical experiments (i.e. computer simulations) of a vibrating string that included a non-linear term (quadratic in one test, cubic in another, and a piecewise linear approximation to a cubic in a third). They found that the behavior of the system was quite different from what intuition would have led them to expect. Fermi thought that after many iterations, the system would exhibit thermalization, an ergodic behavior in which the influence of the initial modes of vibration fade and the system becomes more or less random with all modes excited more or less equally
Equipartition theorem
In classical statistical mechanics, the equipartition theorem is a general formula that relates the temperature of a system with its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition...
. Instead, the system exhibited a very complicated quasi-periodic behavior. They published their results in a Los Alamos technical report in 1955. (Note: Enrico Fermi
Enrico Fermi
Enrico Fermi was an Italian-born, naturalized American physicist particularly known for his work on the development of the first nuclear reactor, Chicago Pile-1, and for his contributions to the development of quantum theory, nuclear and particle physics, and statistical mechanics...
died in 1954 and so this technical report was published after Fermi's death.)
The FPU experiment was important both in showing the complexity of nonlinear system behavior and the value of computer simulation in analyzing systems.
The FPU lattice system
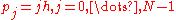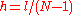Fermi, Pasta and Ulam (FPU) simulated the vibrating string by solving the following discrete system of nearest-neighbor coupled oscillators. We follow the explanation as given in Palais's article. Let there be N oscillators representing a string of length l with equilibrium positions where is the lattice spacing. Then the position of the jth oscillator as a function of is 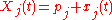so that 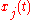gives the displacement from equilibrium. FPU used the following equations of motion: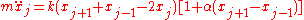(Note: this equation is not equivalent to the classical one given in the French version of the article)
This is just Newton's second law
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
for the jth particle. The first factor
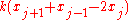is just the usual Hooke's lawHooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
form for the force. The factor with
is the nonlinear force. We can rewrite this in terms of continuum quantities by defining 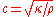to be the wave speed, where 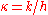is the Young's modulusYoung's modulus
Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
for the string and
is the density: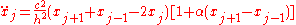Connection to the KdV equation
The continuum limit of the governing equations for the string (with the quadratic force term) is the Korteweg–de Vries equationKorteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
(KdV equation.) The discovery of this relationship and of the soliton
Soliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
solutions of the KdV equation by Kruskal and Zabusky in 1965 was an important step forward in nonlinear system research. We reproduce below a derivation of this limit, which is rather tricky, as found in Palais's article. Beginning from the "continuum form" of the lattice equations above, we first define u(x,t) to be the displacement of the string at position x and time t. We'll then want a correspondence so that
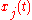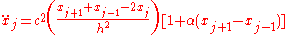
is .We can use Taylor's theorem
Taylor's theorem
In calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
to rewrite the second factor for small
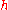, (subscripts of u denote partial derivatives):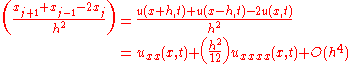.Similarly, the second term in the third factor is:
.Thus, the FPU system is:
.If one were to keep terms up to O(h) only and assume that
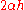approaches a limit, the resulting equation is one which develops shocksShock wave
A shock wave is a type of propagating disturbance. Like an ordinary wave, it carries energy and can propagate through a medium or in some cases in the absence of a material medium, through a field such as the electromagnetic field...
, which is not observed. Thus one keeps the O(h^2) term as well:
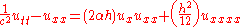.We now make the following substitutions, motivated by the decomposition of traveling wave solutions (of the ordinary wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
, to which this reduces when
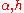vanish) into left- and right-moving waves, so that we only consider a right-moving wave. Let . Under this change of coordinates, the equation becomes: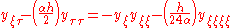.To take the continuum limit, assume that
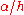tends to a constant and 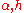tend to zero. If we take 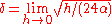, then: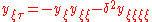.Taking
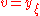results in the KdV equation:.Zabusky and Kruskal argued that it was the fact that soliton solutions of the KdV equation can pass through one another without affecting the asymptotic shapes that explained the quasi-periodicity of the waves in the FPU experiment. In short, thermalization could not occur because of a certain "soliton symmetry" in the system which broke ergodicity.