FTCS scheme
Encyclopedia
In numerical analysis
, the FTCS (Forward-Time Central-Space) method is a finite difference method
used for numerically solving the heat equation
and similar parabolic partial differential equation
s. It is a first-order method in time, explicit
in time, and is conditionally stable
. The abbreviation FTCS was first used by Patrick Roache.
is
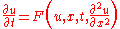
then, letting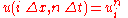
, the forward Euler method is given by:
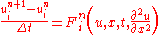
The function
must be discretized spatially with a central difference scheme. This is an explicit method
which means that,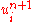
can be explicitly computed (no need of solving a system of algebraic equations) if values of 
at previous time level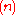 
are known. FTCS method is computationally inexpensive since the method is explicit.
,
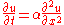
the FTCS scheme is given by:
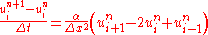
or, letting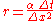
:
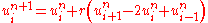
if and only if the following condition is satisfied:
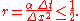
The time step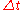
is subjected to the restriction given by the above stability condition. A major drawback of the method is for problems with large diffusivity the time step restriction can be too severe.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, the FTCS (Forward-Time Central-Space) method is a finite difference method
Finite difference method
In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
used for numerically solving the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
and similar parabolic partial differential equation
Parabolic partial differential equation
A parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
s. It is a first-order method in time, explicit
Explicit and implicit methods
Explicit and implicit methods are approaches used in numerical analysis for obtaining numerical solutions of time-dependent ordinary and partial differential equations, as is required in computer simulations of physical processes....
in time, and is conditionally stable
Numerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
. The abbreviation FTCS was first used by Patrick Roache.
The method
The FTCS method is based on central difference in space and the forward Euler method in time, giving first-order convergence in time. For example, in one dimension, if the partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
is
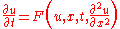
then, letting
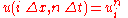, the forward Euler method is given by: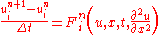The function
must be discretized spatially with a central difference scheme. This is an explicit methodExplicit and implicit methods
Explicit and implicit methods are approaches used in numerical analysis for obtaining numerical solutions of time-dependent ordinary and partial differential equations, as is required in computer simulations of physical processes....
which means that,
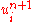can be explicitly computed (no need of solving a system of algebraic equations) if values of at previous time level 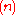are known. FTCS method is computationally inexpensive since the method is explicit.Illustration: one-dimensional heat equation
The FTCS method is often applied to diffusion problems. As an example, for 1D heat equationHeat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
,
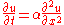
the FTCS scheme is given by:
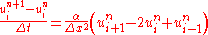
or, letting
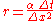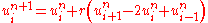
:Stability
The FTCS method, for one-dimensional equations, is numerically stableNumerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
if and only if the following condition is satisfied:
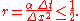
The time step
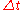is subjected to the restriction given by the above stability condition. A major drawback of the method is for problems with large diffusivity the time step restriction can be too severe.