
Extremum estimator
Encyclopedia
In statistics
and econometrics
, extremum estimators is a wide class of estimator
s for parametric model
s that are calculated through maximization (or minimization) of a certain objective function, which depends on the data. The general theory of extremum estimators was developed by .
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and econometrics
Econometrics
Econometrics has been defined as "the application of mathematics and statistical methods to economic data" and described as the branch of economics "that aims to give empirical content to economic relations." More precisely, it is "the quantitative analysis of actual economic phenomena based on...
, extremum estimators is a wide class of estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
s for parametric model
Parametric model
In statistics, a parametric model or parametric family or finite-dimensional model is a family of distributions that can be described using a finite number of parameters...
s that are calculated through maximization (or minimization) of a certain objective function, which depends on the data. The general theory of extremum estimators was developed by .
Definition
An estimator is called an extremum estimator, if there is an objective function such that-
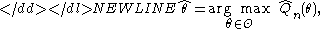
where Θ is the possible range of parameter values. Sometimes a slightly weaker definition is given:-
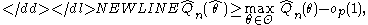
where op(1) is the variable converging in probability to zero. With this modification doesn’t have to be the exact maximizer of the objective function, just be sufficiently close to it.
The theory of extremum estimators does not specify what the objective function should be. There are various types of objective functions suitable for different models, and this framework allows us to analyse the theoretical properties of such estimators from a unified perspective. The theory only specifies the properties that the objective function has to possess, and when one selects a particular objective function, he or she only has to verify that those properties are satisfied.
Consistency
If the set Θ is compact and there is a limiting function Q0(θ) such that: converges to Q0(θ) in probability uniformly over Θ, and the function Q0(θ) is continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
and has a unique maximum at θ = θ0. If these conditions are satisfied then is consistentConsistent estimatorIn statistics, a sequence of estimators for parameter θ0 is said to be consistent if this sequence converges in probability to θ0...
for θ0.
The uniform convergence in probability of means that-

The requirement for Θ to be compact can be replaced with a weaker assumption that the maximum of Q0 was well-separated, that is there should not exist any points θ that are distant from θ0 but such that Q0(θ) were close to Q0(θ0). Formally, it means that for any sequence {θi} such that , it should be true that .
Examples
- Maximum likelihoodMaximum likelihoodIn statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimator uses the objective function-
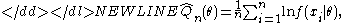
where f(·|θ) is the density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of the distribution from where the observations are drawn.
- Generalized method of moments
Generalized method of momentsIn econometrics, generalized method of moments is a generic method for estimating parameters in statistical models. Usually it is applied in the context of semiparametric models, where the parameter of interest is finite-dimensional, whereas the full shape of the distribution function of the data...
estimator is defined through the objective function-

where g(·|θ) is the moment condition of the model.
- Minimum distance
Minimum distance estimationMinimum distance estimation is a statistical method for fitting a mathematical model to data, usually the empirical distribution.-Definition:...
estimator
- m-estimator
M-estimatorIn statistics, M-estimators are a broad class of estimators, which are obtained as the minima of sums of functions of the data. Least-squares estimators and many maximum-likelihood estimators are M-estimators. The definition of M-estimators was motivated by robust statistics, which contributed new...
s
- Minimum distance
- Generalized method of moments
-
- Maximum likelihood
-
-

