
Expansive
Encyclopedia
In mathematics
, the notion of expansivity formalizes the notion of points moving away from one-another under the action of an iterated function
. The idea of expansivity is fairly rigid
, as the definition of positive expansivity, below, as well as the Schwarz-Ahlfors-Pick theorem demonstrate.
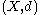 is a metric space
is a metric space
, a homeomorphism
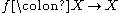 is said to be expansive if there is a constant
is said to be expansive if there is a constant
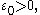
called the expansivity constant, such that for any pair of points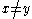 in
in 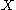 there is an integer
there is an integer  such that
such that
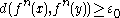 .
.
Note that in this definition, can be positive or negative, and so
can be positive or negative, and so 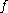 may be expansive in the forward or backward directions.
may be expansive in the forward or backward directions.
The space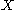 is often assumed to be compact
is often assumed to be compact
, since under that
assumption expansivity is a topological property; i.e. if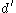 is any other metric generating the same topology as
is any other metric generating the same topology as 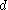 , and if
, and if 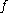 is expansive in
is expansive in 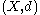 , then
, then 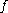 is expansive in
is expansive in 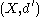 (possibly with a different expansivity constant).
(possibly with a different expansivity constant).
If
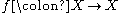
is a continuous map, we say that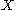 is positively expansive (or forward expansive) if there is a
is positively expansive (or forward expansive) if there is a

such that, for any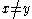 in
in 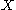 , there is an
, there is an 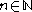 such that
such that  .
.
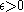 and
and 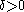 there is an
there is an 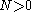 such that for each pair
such that for each pair  of points of
of points of 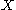 such that
such that 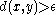 , there is an
, there is an 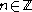 with
with 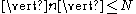 such that
such that
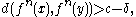
where is the expansivity constant of
is the expansivity constant of 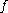 (proof).
(proof).
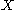 is compact and
is compact and 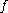 is a positively
is a positively
expansive homeomorphism, then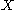 is finite (proof).
is finite (proof).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the notion of expansivity formalizes the notion of points moving away from one-another under the action of an iterated function
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
. The idea of expansivity is fairly rigid
Rigid
In mathematics, a rigid collection C of mathematical objects is one in which every c ∈ C is uniquely determined by less information about c than one would expect....
, as the definition of positive expansivity, below, as well as the Schwarz-Ahlfors-Pick theorem demonstrate.
Definition
If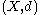 is a metric space
is a metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
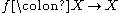 is said to be expansive if there is a constant
is said to be expansive if there is a constant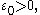
called the expansivity constant, such that for any pair of points
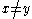 in
in 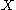 there is an integer
there is an integer  such that
such that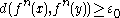 .
.Note that in this definition,
 can be positive or negative, and so
can be positive or negative, and so 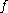 may be expansive in the forward or backward directions.
may be expansive in the forward or backward directions.The space
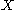 is often assumed to be compact
is often assumed to be compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, since under that
assumption expansivity is a topological property; i.e. if
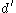 is any other metric generating the same topology as
is any other metric generating the same topology as 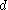 , and if
, and if 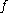 is expansive in
is expansive in 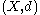 , then
, then 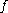 is expansive in
is expansive in 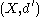 (possibly with a different expansivity constant).
(possibly with a different expansivity constant).If
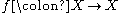
is a continuous map, we say that
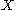 is positively expansive (or forward expansive) if there is a
is positively expansive (or forward expansive) if there is a
such that, for any
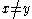 in
in 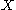 , there is an
, there is an 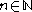 such that
such that  .
.Theorem of uniform expansivity
Given f an expansive homeomorphism, the theorem of uniform expansivity states that for every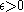 and
and 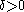 there is an
there is an 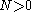 such that for each pair
such that for each pair  of points of
of points of 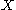 such that
such that 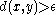 , there is an
, there is an 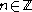 with
with 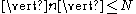 such that
such that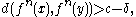
where
 is the expansivity constant of
is the expansivity constant of 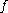 (proof).
(proof).Discussion
Positive expansivity is much stronger than expansivity. In fact, one can prove that if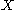 is compact and
is compact and 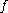 is a positively
is a positivelyexpansive homeomorphism, then
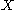 is finite (proof).
is finite (proof).External links
- Expansive dynamical systems on scholarpedia

