
Example of a game without a value
Encyclopedia
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, and in particular the study of zero-sum
Zero-sum
In game theory and economic theory, a zero-sum game is a mathematical representation of a situation in which a participant's gain of utility is exactly balanced by the losses of the utility of other participant. If the total gains of the participants are added up, and the total losses are...
continuous game
Continuous game
A continuous game is a mathematical generalization, used in game theory. It extends the notion of a discrete game, where the players choose from a finite set of pure strategies...
s, it is commonly assumed that a game has a minimax
Minimax
Minimax is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case scenario. Alternatively, it can be thought of as maximizing the minimum gain...
value. This is the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
to one of the players when both play a perfect strategy (which is to choose from a particular PDF
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
).
This article gives an example of a zero sum game that has no value
Minimax
Minimax is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case scenario. Alternatively, it can be thought of as maximizing the minimum gain...
. It is due to Sion and Wolfe.
Zero sum games with a finite number of pure strategies are known to have a minimax
Minimax
Minimax is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case scenario. Alternatively, it can be thought of as maximizing the minimum gain...
value (originally proved by John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
) but this is not necessarily the case if the game has an infinite set of strategies. There follows a simple example of a game with no minimax value.
The existence of such zero-sum games is interesting because many of the results of game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
become inapplicable if there is no minimax value.
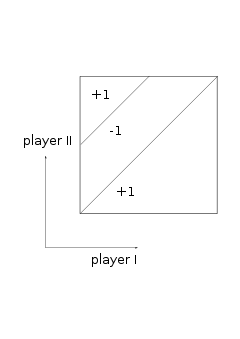
The game
Players I and II choose numbers and
and 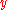 respectively, with
respectively, with  ; the payoff to I is
; the payoff to I is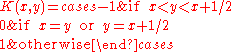
(i.e. player II pays
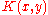 to player I;the game is zero-sum
to player I;the game is zero-sumZero-sum
In game theory and economic theory, a zero-sum game is a mathematical representation of a situation in which a participant's gain of utility is exactly balanced by the losses of the utility of other participant. If the total gains of the participants are added up, and the total losses are...
). Sometimes player I is referred to as the maximizing player and player II the minimizing player.
If
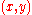 is interpreted as a point on the unit square, the figure shows the payoff to player I. Now suppose that player I adopts a mixed strategy: choosing a number from probability density function (pdf)
is interpreted as a point on the unit square, the figure shows the payoff to player I. Now suppose that player I adopts a mixed strategy: choosing a number from probability density function (pdf)Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
 ; player II chooses from
; player II chooses from 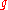 . Player I seeks to maximize the payoff, player II to minimize the payoff. Note that each player is aware of the other's objective.
. Player I seeks to maximize the payoff, player II to minimize the payoff. Note that each player is aware of the other's objective.Interpretation
The game is equivalent to a continuousContinuous game
A continuous game is a mathematical generalization, used in game theory. It extends the notion of a discrete game, where the players choose from a finite set of pure strategies...
Colonel Blotto game
Blotto games
Blotto games constitute a class of two-person zero-sum games in which the players are tasked to simultaneously distribute limited resources over several objects...
. Player I must assign a force x to the attack of one of two mountain passes, and 1-x to the other. Player II must assign a force y to defend the first pass and 1-y to the other, at which is also located an extra defensive force of strength
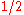 . A player receives from the other a payment of 1 at each pass if his force there exceeds his opponent's, and nothing if they are equal value there (from Sion and Wolfe).
. A player receives from the other a payment of 1 at each pass if his force there exceeds his opponent's, and nothing if they are equal value there (from Sion and Wolfe).Game value
Sion and Wolfe show that
but
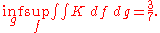
These are the maximal and minimal expectations of the game's value of player I and II respectively.
The
 and
and  respectively take the supremum and infimum over pdf's on the unit interval (actually Probability Borel measures). These represent player I and player II's (mixed) strategies. Thus, player I can assure himself of a payoff of at least
respectively take the supremum and infimum over pdf's on the unit interval (actually Probability Borel measures). These represent player I and player II's (mixed) strategies. Thus, player I can assure himself of a payoff of at least 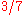 if he knows player II's strategy; and player II can hold the payoff down to
if he knows player II's strategy; and player II can hold the payoff down to 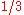 if he knows player I's strategy.
if he knows player I's strategy.There is clearly no epsilon equilibrium for sufficiently small
 , specifically, if
, specifically, if  . Dasgupta and Maskin assert that the game values are achieved if player I puts probability weight only on the set
. Dasgupta and Maskin assert that the game values are achieved if player I puts probability weight only on the set  and player II puts weight only on
and player II puts weight only on 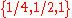 .
.Glicksberg's theorem
Glicksberg's theorem
In the study of zero sum games, Glicksberg's theorem is a result that shows certain games have a minimax value....
shows that any zero-sum game with upper or lower semicontinuous payoff function has a value (in this context, an upper (lower) semicontinuous function K is one in which the set
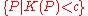 (resp
(resp  ) is open
) is openOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
for any real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
c).
Observe that the payoff function of Sion and Wolfe's example is clearly not semicontinuous. However, it may be made so by changing the value of K(x,x) and K(x,x+1/2) [ie the payoff along the two discontinuities] to either +1 or -1, making the payoff upper or lower semicontinuous respectively. If this is done, the game then has a value.

