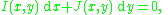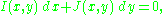Exact differential equation
Encyclopedia
In mathematics, an exact differential equation or total differential equation is a certain kind of ordinary differential equation
which is widely used in physics
and engineering
.
subset D of R2 and two functions I and J which are continuous
on D then an implicit first-order ordinary differential equation
of the form
is called exact differential equation if there exists a continuously differentiable function F, called the potential function, so that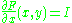
and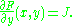
The nomenclature of "exact differential equation" refers to the exact derivative
of a function. For a function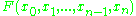 , the exact or total derivative with respect to
, the exact or total derivative with respect to 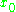 is given by
is given by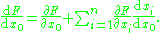
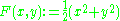
is a potential function for the differential equation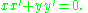
then provides us with a necessary
criterion for the existence of a potential function. For differential equations defined on simply connected sets the criterion is even sufficient and we get the following theorem:
Given a differential equation of the form (for example, when F has zero slope in the x and y direction at F(x,y) ):
with I and J continuously differentiable on a simply connected and open subset D of R2 then a potential function F exists if and only if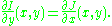
there exists real number
c so that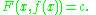
For an initial value problem
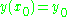
we can locally find a potential function by
Solving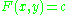
for y, where c is a real number, we can then construct all solutions.
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
which is widely used in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
.
Definition
Given a simply connected and openOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
subset D of R2 and two functions I and J which are continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
on D then an implicit first-order ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
of the form
is called exact differential equation if there exists a continuously differentiable function F, called the potential function, so that
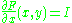
and
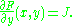
The nomenclature of "exact differential equation" refers to the exact derivative
Total derivative
In the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
of a function. For a function
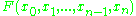 , the exact or total derivative with respect to
, the exact or total derivative with respect to 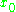 is given by
is given by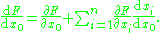
Example
The function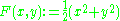
is a potential function for the differential equation
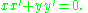
Existence of potential functions
In physical applications the functions I and J are usually not only continuous but even continuously differentiable. Schwarz's TheoremSymmetry of second derivatives
In mathematics, the symmetry of second derivatives refers to the possibility of interchanging the order of taking partial derivatives of a functionfof n variables...
then provides us with a necessary
Necessary and sufficient conditions
In logic, the words necessity and sufficiency refer to the implicational relationships between statements. The assertion that one statement is a necessary and sufficient condition of another means that the former statement is true if and only if the latter is true.-Definitions:A necessary condition...
criterion for the existence of a potential function. For differential equations defined on simply connected sets the criterion is even sufficient and we get the following theorem:
Given a differential equation of the form (for example, when F has zero slope in the x and y direction at F(x,y) ):
with I and J continuously differentiable on a simply connected and open subset D of R2 then a potential function F exists if and only if
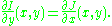
Solutions to exact differential equations
Given an exact differential equation defined on some simply connected and open subset D of R2 with potential function F then a differentiable function f with (x, f(x)) in D is a solution if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there exists real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
c so that
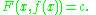
For an initial value problem
Initial value problem
In mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...
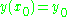
we can locally find a potential function by

Solving
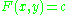
for y, where c is a real number, we can then construct all solutions.