Euler's laws
Encyclopedia
Euler's laws of motion, formulated by Leonhard Euler
about 50 years after Isaac Newton
formulated his laws
about the motion of particles, extends them to rigid body
motion.
is equal to the product of the mass of the body and the velocity of its center of mass
:
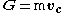. Internal forces, between the particles that make up a body, do not contribute to changing the total momentum of the body. The law is also stated as 
.
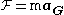about a point,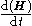
, is equal to the sum of the external moments
about that point: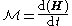
. For rigid bodies translating and rotating in only 2D, this can be expressed as 
, where rcm is the position vector of the center of mass with respect to the point about which moments are summed.
of conservation of linear momentum and angular momentum
, which normally are applied to a mass particle but are extended in continuum mechanics
to a body of continuously distributed mass. For continuous bodies these laws are called Euler’s laws of motion. If a body is represented as an assemblage of discrete particles, each governed by Newton’s laws of motion, then Euler’s equations can be derived from Newton’s laws. Euler’s equations can, however, be taken as axioms describing the laws of motion for extended bodies, independently of any particle structure.
The total body force applied to a continuous body with mass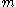
and volume 
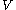is expressed as
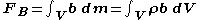
where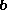
is the body force "density".
Body forces and contact forces acting on the body lead to corresponding moments of force (torque
s) relative to a given point. Thus, the total applied torque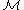
about the origin is given by
where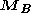
and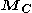 
indicate moments caused by body and contact forces, respectively.
Thus, the sum of all applied forces and torques (with respect to the origin of the coordinate system) in the body can be given by
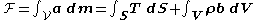
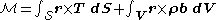
Let the coordinate system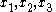
be an inertial frame of reference
. Let
be the position vector of a particle or point 
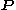in the continuous body with respect to the origin of the coordinate system, and 
the velocity vector of point 
.
Euler’s first axiom or law (law of balance of linear momentum or balance of forces) states that in an inertial frame the time rate of change of linear momentum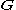
of an arbitrary portion of a continuous body is equal to the total applied force 
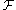acting on the considered portion, and it is expressed as
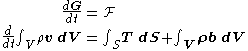
Euler’s second axiom or law (law of balance of angular momentum or balance of torques) states that in an inertial frame the time rate of change of angular momentum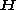
of an arbitrary portion of a continuous body is equal to the total applied torque 
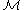acting on the considered portion, and it is expressed as
The derivatives of
and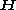 
are material derivatives.
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
about 50 years after Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
formulated his laws
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
about the motion of particles, extends them to rigid body
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
motion.
Euler's first law
Euler's first law states that the linear momentum of a body, is equal to the product of the mass of the body and the velocity of its center of massCenter of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
:
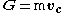. Internal forces, between the particles that make up a body, do not contribute to changing the total momentum of the body. The law is also stated as 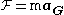.Euler's second law
Euler's second law states that the rate of change of angular momentumAngular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
about a point,
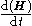, is equal to the sum of the external momentsMoment (physics)
In physics, the term moment can refer to many different concepts:*Moment of force is the tendency of a force to twist or rotate an object; see the article torque for details. This is an important, basic concept in engineering and physics. A moment is valued mathematically as the product of the...
about that point:
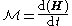. For rigid bodies translating and rotating in only 2D, this can be expressed as , where rcm is the position vector of the center of mass with respect to the point about which moments are summed.Explanation and derivation
The density of internal forces at every point in a deformable body are not necessarily equal, i.e. there is a distribution of stresses throughout the body. This variation of internal forces throughout the body is governed by Newton's second law of motionNewton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
of conservation of linear momentum and angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
, which normally are applied to a mass particle but are extended in continuum mechanics
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
to a body of continuously distributed mass. For continuous bodies these laws are called Euler’s laws of motion. If a body is represented as an assemblage of discrete particles, each governed by Newton’s laws of motion, then Euler’s equations can be derived from Newton’s laws. Euler’s equations can, however, be taken as axioms describing the laws of motion for extended bodies, independently of any particle structure.
The total body force applied to a continuous body with mass
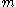and volume 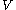is expressed as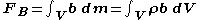where
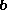is the body force "density".Body forces and contact forces acting on the body lead to corresponding moments of force (torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
s) relative to a given point. Thus, the total applied torque
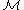about the origin is given bywhere
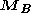and 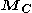indicate moments caused by body and contact forces, respectively.Thus, the sum of all applied forces and torques (with respect to the origin of the coordinate system) in the body can be given by
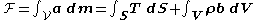
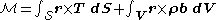
Let the coordinate system
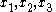be an inertial frame of referenceInertial frame of reference
In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
. Let
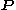be the position vector of a particle or point in the continuous body with respect to the origin of the coordinate system, and the velocity vector of point .Euler’s first axiom or law (law of balance of linear momentum or balance of forces) states that in an inertial frame the time rate of change of linear momentum
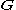of an arbitrary portion of a continuous body is equal to the total applied force 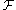acting on the considered portion, and it is expressed as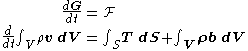Euler’s second axiom or law (law of balance of angular momentum or balance of torques) states that in an inertial frame the time rate of change of angular momentum
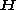of an arbitrary portion of a continuous body is equal to the total applied torque 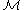acting on the considered portion, and it is expressed asThe derivatives of
and 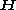are material derivatives.