
Euler's equations
Encyclopedia
- This page discusses rigid body dynamicsRigid body dynamicsIn physics, rigid body dynamics is the study of the motion of rigid bodies. Unlike particles, which move only in three degrees of freedom , rigid bodies occupy space and have geometrical properties, such as a center of mass, moments of inertia, etc., that characterize motion in six degrees of...
. For other uses, see Euler function (disambiguation).
In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, Euler's equations describe the rotation of a rigid body
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
in a frame of reference fixed in the rotating body and having its axes parallel to the body's principal axes of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
.
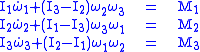
where
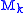 are the components of the applied torque
are the components of the applied torqueTorque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
s,
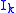 are the principal moments of inertia
are the principal moments of inertiaMoment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
and
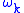 are the components of the angular velocity
are the components of the angular velocityAngular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
vector
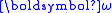 along the principal axes.
along the principal axes.Motivation and derivation
In an inertial frame of referenceInertial frame of reference
In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
(`in'), the time derivative of angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
equals the applied torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
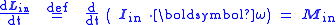
where
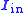 is the moment of inertia
is the moment of inertiaMoment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
tensor calculated in the inertial frame. Although
this law is universally true, it is not always helpful in solving for the motion of a general rotating rigid body, since both
 and
and can change during the motion.
can change during the motion.Therefore, we change to a coordinate frame fixed in the rotating body, and chosen so that its axes are aligned with the principal axes of the moment of inertia tensor
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
. In this frame, at least the moment of inertia tensor is constant (and diagonal), which simplifies calculations. As described in the moment of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
, the angular momentum vector
 can be written
can be written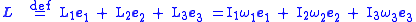
where the
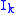 are the principal moments of inertia, the
are the principal moments of inertia, the 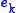 are unit vectors in the directions of the principal axes, and the
are unit vectors in the directions of the principal axes, and the 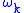 are the components of the angular velocity vector along the principal axes. In a rotating reference frame, the time derivative must be replaced with (see Time derivative in rotating reference frame)
are the components of the angular velocity vector along the principal axes. In a rotating reference frame, the time derivative must be replaced with (see Time derivative in rotating reference frame)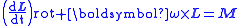
where the
 subscript indicates that it is taken in the rotating reference frame. The expressions for the torque in the rotating and inertial frames are related by
subscript indicates that it is taken in the rotating reference frame. The expressions for the torque in the rotating and inertial frames are related by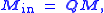
where
 is the rotation tensor, an orthogonal tensor
is the rotation tensor, an orthogonal tensorOrthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
related to the angular velocity vector by
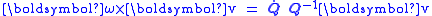 for any vector
for any vector  .
.In general,
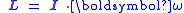 is substituted and the time derivatives are taken realizing that the inertia tensor, and so also the principal moments, do not depend on time. This leads to the general vector form of Euler's equations
is substituted and the time derivatives are taken realizing that the inertia tensor, and so also the principal moments, do not depend on time. This leads to the general vector form of Euler's equations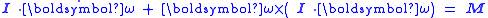
For principal axis rotation
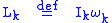 is substituted, and then taking the cross product and using the fact that the principal moments do not change with time, we arrive at the Euler equations
is substituted, and then taking the cross product and using the fact that the principal moments do not change with time, we arrive at the Euler equations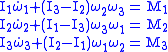
Torque-free solutions
For the RHSs equal to zero there are non-trivial solutions: torque-free precessionPrecession
Precession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
. Notice that if I is constant (because the inertia tensor is the identity, because we work in the intrinsic frame, or because the torque is driving the rotation around the same axis
 so that
so that 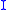 is not changing) then we may write
is not changing) then we may write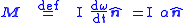
where
 is called the angular acceleration
is called the angular accelerationAngular acceleration
Angular acceleration is the rate of change of angular velocity over time. In SI units, it is measured in radians per second squared , and is usually denoted by the Greek letter alpha .- Mathematical definition :...
(or rotational acceleration) about the rotation axis
 .
.But if I is not constant in the external reference frame (ie. the body is moving and its inertia tensor is not the identity) then we cannot take the I outside the derivate. In this cases we will have torque-free precession, in such a way that I(t) and w(t) change together so that their derivative is zero. This motion can be visualized by Poinsot's construction
Poinsot's construction
In classical mechanics, Poinsot's construction is a geometrical method for visualizing the torque-free motion of a rotating rigid body, that is, the motion of a rigid body on which no external forces are acting. This motion has four constants: the kinetic energy of the body and the three components...
.
Generalizations
It is also possible to use these equations if the axes in which is described are not connected to the body.
is described are not connected to the body. 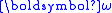 should then be replaced with the rotation of the axes instead of the rotation of the body. It is, however, still required that the chosen axes are still principal axes of inertia! This form of the Euler equations is handy for rotation-symmetric objects that allow some of the principal axes of rotation to be chosen freely.
should then be replaced with the rotation of the axes instead of the rotation of the body. It is, however, still required that the chosen axes are still principal axes of inertia! This form of the Euler equations is handy for rotation-symmetric objects that allow some of the principal axes of rotation to be chosen freely.See also
- Moment of inertiaMoment of inertiaIn classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
- Poinsot's constructionPoinsot's constructionIn classical mechanics, Poinsot's construction is a geometrical method for visualizing the torque-free motion of a rotating rigid body, that is, the motion of a rigid body on which no external forces are acting. This motion has four constants: the kinetic energy of the body and the three components...
- Euler anglesEuler anglesThe Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
- Rigid rotorRigid rotorThe rigid rotor is a mechanical model that is used to explain rotating systems.An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space three angles are required. A special rigid rotor is the linear rotor which isa 2-dimensional object, requiring...

