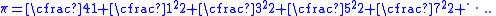Euler's continued fraction formula
Encyclopedia
In the analytic theory
of continued fractions
, Euler's continued fraction formula is an identity connecting a certain very general infinite series with an infinite continued fraction. First published in 1748, it was at first regarded as a simple identity connecting a finite sum with a finite continued fraction in such a way that the extension to the infinite case was immediately apparent. Today it is more fully appreciated as a useful tool in analytic attacks on the general convergence problem for infinite continued fractions with complex elements.
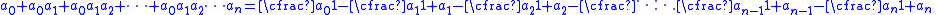
The identity is easily established by induction
on n, and is therefore applicable in the limit: if the expression on the left is extended to represent a convergent infinite series, the expression on the right can also be extended to represent a convergent infinite continued fraction.
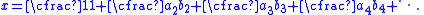
is a continued fraction with complex elements
and none of the denominators Bi are zero, a sequence of ratios {ri} can be defined by
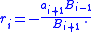
For x and ri so defined, these equalities can be proved by induction.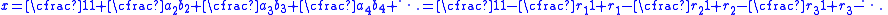
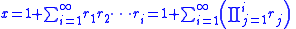
Here equality is to be understood as equivalence, in the sense that the nth convergent
of each continued fraction is equal to the nth partial sum of the series shown above. So if the series shown is convergent – or uniformly convergent, when the ais and bis are functions of some complex variable z – then the continued fractions also converge, or converge uniformly.
with a power series expansion that converges uniformly on every bounded domain in the complex plane.
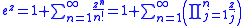
The application of Euler's continued fraction formula is straightforward:
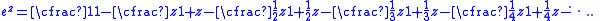
Applying an equivalence transformation that consists of clearing the fractions this example is simplified to
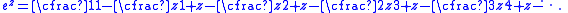
and we can be certain that this continued fraction converges uniformly on every bounded domain in the complex plane because it is equivalent to the power series for ez.
of the natural logarithm in the neighborhood of z = 1 is well known. Recognizing that log(a/b) = log(a) - log(b), the following series is easily derived:
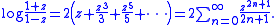
This series converges when |z| < 1 and can also be expressed as a sum of products:
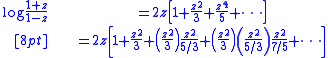
Applying Euler's continued fraction formula to this expression shows that

and using an equivalence transformation to clear all the fractions results in
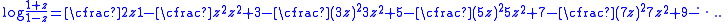
This continued fraction converges when |z| < 1 because it is equivalent to the series from which it was derived.
. First we note that
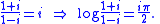
Setting z = i in the previous result, and remembering that i2 = −1, we obtain immediately
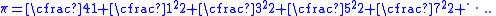
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
of continued fractions
Generalized continued fraction
In complex analysis, a branch of mathematics, a generalized continued fraction is a generalization of regular continued fractions in canonical form, in which the partial numerators and partial denominators can assume arbitrary real or complex values....
, Euler's continued fraction formula is an identity connecting a certain very general infinite series with an infinite continued fraction. First published in 1748, it was at first regarded as a simple identity connecting a finite sum with a finite continued fraction in such a way that the extension to the infinite case was immediately apparent. Today it is more fully appreciated as a useful tool in analytic attacks on the general convergence problem for infinite continued fractions with complex elements.
The original formula
Euler derived the formula as an identity connecting a finite sum of products with a finite continued fraction.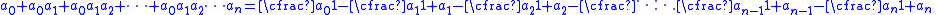
The identity is easily established by induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
on n, and is therefore applicable in the limit: if the expression on the left is extended to represent a convergent infinite series, the expression on the right can also be extended to represent a convergent infinite continued fraction.
Euler's formula in modern notation
If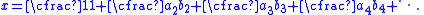
is a continued fraction with complex elements
Generalized continued fraction
In complex analysis, a branch of mathematics, a generalized continued fraction is a generalization of regular continued fractions in canonical form, in which the partial numerators and partial denominators can assume arbitrary real or complex values....
and none of the denominators Bi are zero, a sequence of ratios {ri} can be defined by
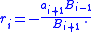
For x and ri so defined, these equalities can be proved by induction.
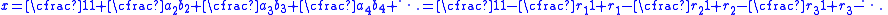
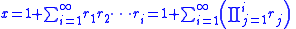
Here equality is to be understood as equivalence, in the sense that the nth convergent
Convergent (continued fraction)
A convergent is one of a sequence of values obtained by evaluating successive truncations of a continued fraction The nth convergent is also known as the nth approximant of a continued fraction.-Representation of real numbers:...
of each continued fraction is equal to the nth partial sum of the series shown above. So if the series shown is convergent – or uniformly convergent, when the ais and bis are functions of some complex variable z – then the continued fractions also converge, or converge uniformly.
The exponential function
The exponential function ez is an entire functionEntire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
with a power series expansion that converges uniformly on every bounded domain in the complex plane.
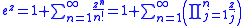
The application of Euler's continued fraction formula is straightforward:
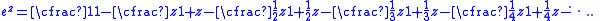
Applying an equivalence transformation that consists of clearing the fractions this example is simplified to
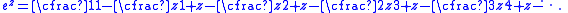
and we can be certain that this continued fraction converges uniformly on every bounded domain in the complex plane because it is equivalent to the power series for ez.
The natural logarithm
The Taylor series for the principal branchPrincipal branch
In mathematics, a principal branch is a function which selects one branch, or "slice", of a multi-valued function. Most often, this applies to functions defined on the complex plane: see branch cut....
of the natural logarithm in the neighborhood of z = 1 is well known. Recognizing that log(a/b) = log(a) - log(b), the following series is easily derived:
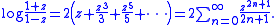
This series converges when |z| < 1 and can also be expressed as a sum of products:
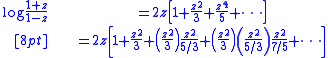
Applying Euler's continued fraction formula to this expression shows that

and using an equivalence transformation to clear all the fractions results in
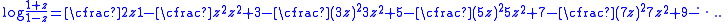
This continued fraction converges when |z| < 1 because it is equivalent to the series from which it was derived.
A continued fraction for π
We can use the previous example involving the principal branch of the natural logarithm function to construct a continued fraction representation of πPi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
. First we note that
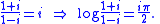
Setting z = i in the previous result, and remembering that i2 = −1, we obtain immediately