
Equipollence (geometry)
Encyclopedia
In geometry
, equipollence is a certain relationship between ordered pairs of points. A pair (a, b) of points and another pair (c, d) are equipollent precisely if the distance and direction from a to b are respectively the same as the distance and direction from c to d.
(which may be the field R of real number
s). An affine space
E associated with a K-vector space V is a set provided with a mapping ƒ : E × E → V; (a, b) → ƒ(a, b) (the vector ƒ(a b) will be denoted ) such that:
) such that:
1) for all a in E and all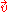 in V there exist a single b in E such that
in V there exist a single b in E such that 
2) for all a,b,c in E,
Definition:
Two bipoints (a, b) and (c, d) of ExE are equipollent if

when K=R (or K is a field of characteristic different from 2) then (a, b) and (c, d) are equipollent if and only if (a,d) and (b,c) have the same midpoint.
The concept of equipollence of bipoints can be also defined axiomatically.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, equipollence is a certain relationship between ordered pairs of points. A pair (a, b) of points and another pair (c, d) are equipollent precisely if the distance and direction from a to b are respectively the same as the distance and direction from c to d.
In affine spaces over a field
Let K be a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
(which may be the field R of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s). An affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
E associated with a K-vector space V is a set provided with a mapping ƒ : E × E → V; (a, b) → ƒ(a, b) (the vector ƒ(a b) will be denoted
 ) such that:
) such that:1) for all a in E and all
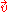 in V there exist a single b in E such that
in V there exist a single b in E such that 
2) for all a,b,c in E,

Definition:
Two bipoints (a, b) and (c, d) of ExE are equipollent if

when K=R (or K is a field of characteristic different from 2) then (a, b) and (c, d) are equipollent if and only if (a,d) and (b,c) have the same midpoint.
The concept of equipollence of bipoints can be also defined axiomatically.

