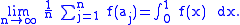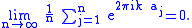Equidistributed sequence
Encyclopedia
In mathematics
, a bounded sequence {s1, s2, s3, …} of real number
s is said to be equidistributed, or uniformly distributed, if the proportion of terms falling in a subinterval is proportional to the length of that interval. Such sequences are studied in Diophantine approximation
theory and have applications to Monte Carlo integration.
s is said to be equidistributed on an interval [a, b] if for any subinterval [c, d] of [a, b] we have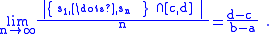
(Here, the notation |{s1,…,sn }∩[c,d]| denotes the number of elements, out of the first n elements of the sequence, that are between c and d.)
For example, if a sequence is equidistributed in [0, 2], since the interval [0.5, 0.9] occupies 1/5 of the length of the interval [0, 2], as n becomes large, the proportion of the first n members of the sequence which fall between 0.5 and 0.9 must approach 1/5. Loosely speaking, one could say that each member of the sequence is equally likely to fall anywhere in its range. However, this is not to say that {sn} is a sequence of random variables; rather, it is a determinate sequence of real numbers.

A sequence is thus equidistributed if the discrepancy D(N) tends to zero as N tends to infinity.
Equidistribution is a rather weak criterion to express the fact that a sequence fills the segment leaving no gaps. For example, the drawings of a random variable uniform over a segment will be equidistributed in the segment, but there will be large gaps compared to a sequence which first enumerates multiples of ε in the segment, for some small ε, in an appropriately chosen way, and then continues to do this for smaller and smaller values of ε. See low-discrepancy sequence
for stronger criteria and constructions of low-discrepancy sequences for constructions of sequences which are more evenly distributed.
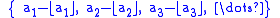
is equidistributed in the interval [0, 1].
is uniformly distributed modulo 1: this is the equidistribution theorem
.
is equidistributed modulo 1. This is a famous theorem
of analytic number theory
, proved by I. M. Vinogradov in 1935.
The third condition is known as Weyl's criterion
. Together with the formula for the sum of a finite geometric series, the equivalence of the first and third conditions furnishes an immediate proof of the equidistribution theorem.
values of some parameter α: that is, for values of α not lying in some exceptional set of Lebesgue measure
zero.
It is not known whether the sequences {en} or {πn} are equidistributed mod 1. However it is known that the sequence {αn} is not equidistributed mod 1 if α is a PV number.
s is said to be well-distributed on [a, b] if for any subinterval [c, d] of [a, b] we have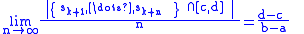
uniformly in k. Clearly every well-distributed sequence is uniformly distributed, but the converse does not hold. The definition of well-distributed modulo 1 is analogous.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a bounded sequence {s1, s2, s3, …} of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s is said to be equidistributed, or uniformly distributed, if the proportion of terms falling in a subinterval is proportional to the length of that interval. Such sequences are studied in Diophantine approximation
Diophantine approximation
In number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
theory and have applications to Monte Carlo integration.
Definition
A bounded sequence {s1, s2, s3, …} of real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s is said to be equidistributed on an interval [a, b] if for any subinterval [c, d] of [a, b] we have
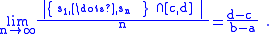
(Here, the notation |{s1,…,sn }∩[c,d]| denotes the number of elements, out of the first n elements of the sequence, that are between c and d.)
For example, if a sequence is equidistributed in [0, 2], since the interval [0.5, 0.9] occupies 1/5 of the length of the interval [0, 2], as n becomes large, the proportion of the first n members of the sequence which fall between 0.5 and 0.9 must approach 1/5. Loosely speaking, one could say that each member of the sequence is equally likely to fall anywhere in its range. However, this is not to say that {sn} is a sequence of random variables; rather, it is a determinate sequence of real numbers.
Discrepancy
We define the discrepancy D(N) for a sequence {s1, s2, s3, …} with respect to the interval [a, b] as
A sequence is thus equidistributed if the discrepancy D(N) tends to zero as N tends to infinity.
Equidistribution is a rather weak criterion to express the fact that a sequence fills the segment leaving no gaps. For example, the drawings of a random variable uniform over a segment will be equidistributed in the segment, but there will be large gaps compared to a sequence which first enumerates multiples of ε in the segment, for some small ε, in an appropriately chosen way, and then continues to do this for smaller and smaller values of ε. See low-discrepancy sequence
Low-discrepancy sequence
In mathematics, a low-discrepancy sequence is a sequence with the property that for all values of N, its subsequence x1, ..., xN has a low discrepancy....
for stronger criteria and constructions of low-discrepancy sequences for constructions of sequences which are more evenly distributed.
Equidistribution modulo 1
The sequence {a1, a2, a3, …} is said to be equidistributed modulo 1 or uniformly distributed modulo 1 if the sequence of the fractional parts of the an's, (denoted by an−⌊an⌋)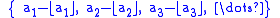
is equidistributed in the interval [0, 1].
Examples
- The sequence of all multiples of an irrational α,
-
- 0, α, 2α, 3α, 4α, …
is uniformly distributed modulo 1: this is the equidistribution theorem
Equidistribution theorem
In mathematics, the equidistribution theorem is the statement that the sequenceis uniformly distributed on the unit interval, when a is an irrational number...
.
- More generally, if p is a polynomial with at least one irrational coefficient (other than the constant term) then the sequence p(n) is uniformly distributed modulo 1: this was proved by Weyl and is an application of the theorem of Johannes van der CorputJohannes van der CorputJohannes Gualtherus van der Corput was a Dutch mathematician, working in the field of analytic number theory....
. - The sequence log(n) is not uniformly distributed modulo 1.
- The sequence of all multiples of an irrational α by successive prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s,
-
- 2α, 3α, 5α, 7α, 11α, …
is equidistributed modulo 1. This is a famous theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
of analytic number theory
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
, proved by I. M. Vinogradov in 1935.
- The van der Corput sequenceVan der Corput sequenceA van der Corput sequence is a low-discrepancy sequence over the unit interval first published in 1935 by the Dutch mathematician J. G. van der Corput. It is constructed by reversing the base n representation of the sequence of natural numbers...
is equidistributed.
Properties
The following three conditions are equivalent:- {an} is equidistributed modulo 1.
- For every Riemann integrable function f on [0, 1],
- For every nonzero integer k,
-
The third condition is known as Weyl's criterion
Weyl's criterion
In mathematics, in the theory of diophantine approximation, Weyl's criterion states that a sequence of real numbers is equidistributed mod 1 if and only if for all non-zero integers \ell we have:...
. Together with the formula for the sum of a finite geometric series, the equivalence of the first and third conditions furnishes an immediate proof of the equidistribution theorem.
Metric theorems
Metric theorems describe the behaviour of a parametrised sequence for almost allAlmost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
values of some parameter α: that is, for values of α not lying in some exceptional set of Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
zero.
- For any sequence of distinct integers bn, the sequence {bn α} is equidistributed mod 1 for almost all values of α.
- The sequence {αn} is equidistributed mod 1 for almost all values of α > 1.
It is not known whether the sequences {en} or {πn} are equidistributed mod 1. However it is known that the sequence {αn} is not equidistributed mod 1 if α is a PV number.
Well-distributed sequence
A bounded sequence {s1, s2, s3, …} of real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s is said to be well-distributed on [a, b] if for any subinterval [c, d] of [a, b] we have
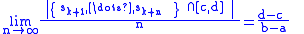
uniformly in k. Clearly every well-distributed sequence is uniformly distributed, but the converse does not hold. The definition of well-distributed modulo 1 is analogous.