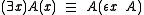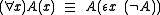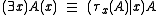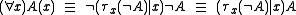Epsilon calculus
Encyclopedia
Hilbert
's epsilon calculus is an extension of a formal language
by the epsilon operator, where the epsilon operator substitutes for quantifiers
in that language as a method leading to a proof of consistency
for the extended formal language. The epsilon operator and epsilon substitution method are typically applied to a first-order predicate calculus
, followed by a showing of consistency. The epsilon-extended calculus is further extended and generalized to cover those mathematical objects, classes, and categories for which there is a desire to show consistency, building on previously-shown consistency at earlier levels.
The intended interpretation of εx A is some x that satisfies A, if it exists. In other words, εx A returns some term t such that A(t) is true, otherwise it returns some default or arbitrary term. If more than one term can satisfy A, then any one of these terms (which make A true) can be chosen, non-deterministically. Equality is required to be defined under L, and the only rules required for L extended by the epsilon operator are modus ponens and the substitution of A(t) to replace A(x) for any term t.
where A is a relation in L, x is a variable, and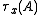 juxtaposes a
juxtaposes a  at the front of A, replaces all instances of x with
at the front of A, replaces all instances of x with  , and links them back to
, and links them back to  . Then let Y be an assembly, (Y|x)A denotes the replacement of all variables x in A with Y.
. Then let Y be an assembly, (Y|x)A denotes the replacement of all variables x in A with Y.
This notation is equivalent to the Hilbert notation and is read the same.
s as consistent in relation to constructive or semi-constructive systems. While Gödel's results on incompleteness mooted Hilbert's Program to a great extent, modern researchers find the epsilon calculus to provide alternatives for approaching proofs of systemic consistency as described in the epsilon substitution method.
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
's epsilon calculus is an extension of a formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
by the epsilon operator, where the epsilon operator substitutes for quantifiers
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
in that language as a method leading to a proof of consistency
Consistency proof
In logic, a consistent theory is one that does not contain a contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if and only if it has a model, i.e. there exists an interpretation under which all...
for the extended formal language. The epsilon operator and epsilon substitution method are typically applied to a first-order predicate calculus
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, followed by a showing of consistency. The epsilon-extended calculus is further extended and generalized to cover those mathematical objects, classes, and categories for which there is a desire to show consistency, building on previously-shown consistency at earlier levels.
Hilbert notation
For any formal language L, extend L by adding the epsilon operator to redefine quantification:The intended interpretation of εx A is some x that satisfies A, if it exists. In other words, εx A returns some term t such that A(t) is true, otherwise it returns some default or arbitrary term. If more than one term can satisfy A, then any one of these terms (which make A true) can be chosen, non-deterministically. Equality is required to be defined under L, and the only rules required for L extended by the epsilon operator are modus ponens and the substitution of A(t) to replace A(x) for any term t.
Bourbaki notation
In tau-square notation from N. Bourbaki's Theory of Sets, the quantifiers are defined as follows:where A is a relation in L, x is a variable, and
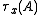 juxtaposes a
juxtaposes a  at the front of A, replaces all instances of x with
at the front of A, replaces all instances of x with  , and links them back to
, and links them back to  . Then let Y be an assembly, (Y|x)A denotes the replacement of all variables x in A with Y.
. Then let Y be an assembly, (Y|x)A denotes the replacement of all variables x in A with Y.This notation is equivalent to the Hilbert notation and is read the same.
Modern approaches
Hilbert's Program for mathematics was to justify those formal systemFormal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
s as consistent in relation to constructive or semi-constructive systems. While Gödel's results on incompleteness mooted Hilbert's Program to a great extent, modern researchers find the epsilon calculus to provide alternatives for approaching proofs of systemic consistency as described in the epsilon substitution method.