
Entropy estimation
Encyclopedia
Estimating the differential entropy
of a system or process, given some observations, is useful in various science/engineering applications, such as Independent Component Analysis
, image analysis
, genetic analysis
, speech recognition
, manifold learning, and time delay estimation. The simplest and most common approach uses histogram-based estimation, but other approaches have been developed and used, each with their own benefits and drawbacks. The main factor in choosing a method is often a trade-off between the bias and the variance of the estimate although the nature of the (suspected) distribution of the data may also be a factor.

can be approximated by producing a histogram
of the observations, and then finding the discrete entropy
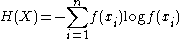
of that histogram (which is itself a maximum-likelihood estimate
of the discretized frequency distribution). Histograms can be quick to calculate, and simple, so this approach has some attractions. However, the estimate produced is bias
ed, and although corrections can be made to the estimate, they may not always be satisfactory.
A method better suited for multidimensional pdf's is to first make a pdf estimate with some method, and then, from the pdf estimate, compute the entropy. A useful pdf estimate method is e.g. Gaussian Mixture Modeling (GMM), where the Expectation Maximization (EM) algorithm is used to find an ML estimate of a weighted sum of Gaussian pdf's approximating the data pdf.
of) the probability density in that region: the closer together the values are, the higher the probability density. This is a very rough estimate with high variance
, but can be improved, for example by thinking about the space between a given value and the one m away from it, where m is some fixed number.
The probability density estimated in this way can then be used to calculate the entropy estimate, in a similar way to that given above for the histogram, but with some slight tweaks.
One of the main drawbacks with this approach is going beyond one dimension: the idea of lining the data points up in order falls apart in more than one dimension. However, using analogous methods, some multidimensional entropy estimators have been developed.
Differential entropy
Differential entropy is a concept in information theory that extends the idea of entropy, a measure of average surprisal of a random variable, to continuous probability distributions.-Definition:...
of a system or process, given some observations, is useful in various science/engineering applications, such as Independent Component Analysis
Independent component analysis
Independent component analysis is a computational method for separating a multivariate signal into additive subcomponents supposing the mutual statistical independence of the non-Gaussian source signals...
, image analysis
Image analysis
Image analysis is the extraction of meaningful information from images; mainly from digital images by means of digital image processing techniques...
, genetic analysis
Genetic analysis
Genetic analysis can be used generally to describe methods both used in and resulting from the sciences of genetics and molecular biology, or to applications resulting from this research....
, speech recognition
Speech recognition
Speech recognition converts spoken words to text. The term "voice recognition" is sometimes used to refer to recognition systems that must be trained to a particular speaker—as is the case for most desktop recognition software...
, manifold learning, and time delay estimation. The simplest and most common approach uses histogram-based estimation, but other approaches have been developed and used, each with their own benefits and drawbacks. The main factor in choosing a method is often a trade-off between the bias and the variance of the estimate although the nature of the (suspected) distribution of the data may also be a factor.
Histogram estimator
The histogram approach uses the idea that the differential entropy,
can be approximated by producing a histogram
Histogram
In statistics, a histogram is a graphical representation showing a visual impression of the distribution of data. It is an estimate of the probability distribution of a continuous variable and was first introduced by Karl Pearson...
of the observations, and then finding the discrete entropy
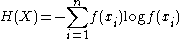
of that histogram (which is itself a maximum-likelihood estimate
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
of the discretized frequency distribution). Histograms can be quick to calculate, and simple, so this approach has some attractions. However, the estimate produced is bias
Bias
Bias is an inclination to present or hold a partial perspective at the expense of alternatives. Bias can come in many forms.-In judgement and decision making:...
ed, and although corrections can be made to the estimate, they may not always be satisfactory.
A method better suited for multidimensional pdf's is to first make a pdf estimate with some method, and then, from the pdf estimate, compute the entropy. A useful pdf estimate method is e.g. Gaussian Mixture Modeling (GMM), where the Expectation Maximization (EM) algorithm is used to find an ML estimate of a weighted sum of Gaussian pdf's approximating the data pdf.
Estimates based on sample-spacings
If the data is one-dimensional, we can imagine taking all the observations and putting them in order of their value. The spacing between one value and the next then gives us a rough idea of (the reciprocalMultiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of) the probability density in that region: the closer together the values are, the higher the probability density. This is a very rough estimate with high variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
, but can be improved, for example by thinking about the space between a given value and the one m away from it, where m is some fixed number.
The probability density estimated in this way can then be used to calculate the entropy estimate, in a similar way to that given above for the histogram, but with some slight tweaks.
One of the main drawbacks with this approach is going beyond one dimension: the idea of lining the data points up in order falls apart in more than one dimension. However, using analogous methods, some multidimensional entropy estimators have been developed.

