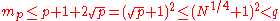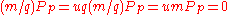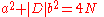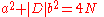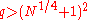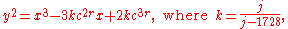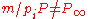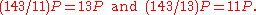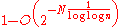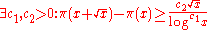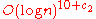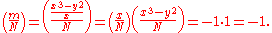Elliptic curve primality testing
Encyclopedia
Elliptic curve
primality testing techniques are among the quickest and most widely used methods in primality proving. It is an idea forwarded by Shafi Goldwasser
and Joe Kilian in 1986 and turned into an algorithm by A.O.L. Atkin the same year. The algorithm was altered and improved by several collaborators subsequently, and notably by Atkin and Francois Morain, in 1993. The concept of using elliptic curves in factorization
had been developed by H.W. Lenstra in 1985, and the implications for its use in primality testing (and proving) followed quickly.
Primality testing is a field that has been around since the time of Fermat, in whose time most algorithms were based on factoring, which become unwieldy with large input; modern algorithms treat the problems of determining whether a number is prime and what its factors are separately. It enjoys a great deal of interest with the advent of modern cryptography. Although many current tests result in a probabilistic output (N is either shown composite, or probably prime, such as with the Miller–Rabin test), the elliptic curve test, proves primality (or compositeness) with a quickly verifiable certificate.
Elliptic curve primality proving provides an alternative to (among others) the Pocklington primality test
, which can be difficult to implement in practice. Interestingly, the elliptic curve primality tests are based on criteria which is analogous to the Pocklington criterion, on which that test is based, where the group
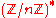 is replaced by
is replaced by 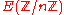 , and E is a properly chosen elliptic curve. We will now state a proposition on which to base our test, which is analogous to the Pocklington criterion, and gives rise to the Goldwasser-Kilian-Atkin form of the elliptic curve primality test.
, and E is a properly chosen elliptic curve. We will now state a proposition on which to base our test, which is analogous to the Pocklington criterion, and gives rise to the Goldwasser-Kilian-Atkin form of the elliptic curve primality test.
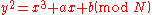 . Consider E over
. Consider E over 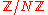 , use the usual addition law on E, and write O for the neutral element on E.
, use the usual addition law on E, and write O for the neutral element on E.
Let m be an integer. If there is a prime q which divides m, and is greater than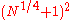 and there exists a point P on E such that
and there exists a point P on E such that
(1) mP = 0
(2) (m/q)P is defined and not equal to 0
Then N is prime.
 that divides N. Define
that divides N. Define 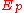 as the elliptic curve defined by the same equation as E but evaluated modulo p rather than modulo N. Define
as the elliptic curve defined by the same equation as E but evaluated modulo p rather than modulo N. Define 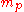 as the order of the group
as the order of the group 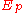 . By Hasse's theorem on elliptic curves we know
. By Hasse's theorem on elliptic curves we know
and thus and there exists an integer u with the property that
and there exists an integer u with the property that
Let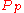 be the point P evaluated modulo p. Thus, on
be the point P evaluated modulo p. Thus, on 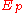 we have
we have
by (1), as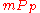 is calculated using the same method as mP, except modulo p rather than modulo N (and
is calculated using the same method as mP, except modulo p rather than modulo N (and  ).
).
This contradicts (2), because if (m/q)P is defined and not equal to 0 (mod N), then the same method calculated modulo p instead of modulo N will yield
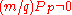
Choose three integers at random, a, x, y and set
Now P = (x,y) is a point on E, where we have that E is defined by . Next we need an algorithm to count the number of points on E. Applied to E, this algorithm (Koblitz and others suggest Schoof's algorithm
. Next we need an algorithm to count the number of points on E. Applied to E, this algorithm (Koblitz and others suggest Schoof's algorithm
) produces a number m which is the number of points on curve E over FN, provided N is prime. Next we have a criterion for deciding whether our curve E is acceptable.
If we can write m in the form where
where  is a small integer and q a probable prime (it has passed some previous probabilistic primality test
is a small integer and q a probable prime (it has passed some previous probabilistic primality test
, for example), then we do not discard E. If it is not possible to write m in this form, we discard our curve and randomly select another triple (a, x, y) to start over.
Assuming we find a curve which passes the criterion, proceed to calculate mP and kP. If at any stage in the calculation we encounter an undefined expression (from calculating the multiples of P or in our point counting algorithm), it gives us a non-trivial factor of N.
If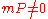 it is clear that N is not prime, because if N were prime then E would have order m, and any element of E would become 0 on multiplication by m. If kP = 0 then we have hit a dead-end and must start again with a different triple.
it is clear that N is not prime, because if N were prime then E would have order m, and any element of E would become 0 on multiplication by m. If kP = 0 then we have hit a dead-end and must start again with a different triple.
Now if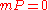 and
and 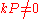 then our previous proposition tells us that N is prime. However there is one possible problem, which is the primality of q. This must be verified, using the same algorithm. So we have described a down-run procedure, where the primality of N can be proven through the primality of q and indeed smaller 'probable primes' until we have reached certain primes and are finished.
then our previous proposition tells us that N is prime. However there is one possible problem, which is the primality of q. This must be verified, using the same algorithm. So we have described a down-run procedure, where the primality of N can be proven through the primality of q and indeed smaller 'probable primes' until we have reached certain primes and are finished.
to be seen in the historical context, before the improvements by Elkies and Atkin to Schoof's method.
A second problem Koblitz notes is the difficulty of finding the curve E whose number of points is of the form kq, as above. There is no known theorem which guarantees we can find a suitable E in polynomially many attempts. The distribution of primes on the Hasse interval
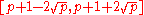 ,
,
which contains m, is not the same as the distribution of primes in the group orders, counting curves with multiplity. However, this is not a significant problem in practice.
is key in the construction of the curve.
Now, given an N for which primality needs to be proven we need to find a suitable m and q, just as in the Goldwasser-Kilian test, that will fulfill the proposition and prove the primality of N. (Of course, a point P and the curve itself, E, must also be found.)
ECPP uses complex multiplication to construct the curve E, doing so in a way that allows for m (the number of points on E) to be easily computed. We will now describe this method:
Utilization of complex multiplication requires a negative discriminant
, D, such that D can be written as the product of two elements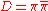 , or completely equivalently, we can write the equation:
, or completely equivalently, we can write the equation:
For some a, b. If we can describe N in terms of either of these forms, we can create an elliptic curve E on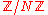 with complex multiplication (described in detail below), and the number of points is given by:
with complex multiplication (described in detail below), and the number of points is given by:
For N to split into two the two elements, we need that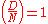 (where
(where 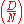 denotes the Legendre symbol
denotes the Legendre symbol
). This is a necessary condition, and we achieve sufficiency if the class number
h(D) of the order in is 1. This happens for only 13 values of D, which are the elements of {−3, −4, −7, −8, −11, −12, −16, −19, −27, −28, −43, −67, −163}
is 1. This happens for only 13 values of D, which are the elements of {−3, −4, −7, −8, −11, −12, −16, −19, −27, −28, −43, −67, −163}
 and whether 4N can be written as:
and whether 4N can be written as:
This part can be verified using Cornacchia's algorithm
. Once acceptable D and a have been discovered, calculate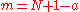 . Now if m has a prime factor q of size
. Now if m has a prime factor q of size
use the complex multplication method to construct the curve E and a point P on it.
Then we can use our proposition to verify the primality of N. Note that if m does not have a large prime factor or cannot be factored quickly enough, another choice of D can be made.
, the way in which an elliptic curve can be created, given our D (which can be written as a product of two elements).
Assume first that and
and 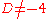 (these cases are much more easily done). It is necessary to calculate the elliptic j-invariant
(these cases are much more easily done). It is necessary to calculate the elliptic j-invariant
s of the h(D) classes of the order of discriminant D as complex numbers. There are several formulas to calculate these.
Next create the monic polynomial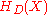 , which has roots corresponding to the h(D) values. Note, that
, which has roots corresponding to the h(D) values. Note, that 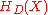 is the class polynomial. From complex multiplication theory, we know that
is the class polynomial. From complex multiplication theory, we know that 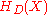 has integer coefficients, which allows us to estimate these coefficients accurately enough to discover their true values.
has integer coefficients, which allows us to estimate these coefficients accurately enough to discover their true values.
Now, if N is prime, CM tells us that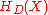 splits modulo N into a product of h(D) linear factors, based on the fact that D was chosen so that N splits as the product of two elements. Now if j is one of the h(D) roots modulo N we can define E as:
splits modulo N into a product of h(D) linear factors, based on the fact that D was chosen so that N splits as the product of two elements. Now if j is one of the h(D) roots modulo N we can define E as:
c is any quadratic nonresidue mod N, and r is either 0 or 1.
Given a root j there are only two possible nonisomorphic choices of E, one for each choice of r. We have the cardinality of these curves as
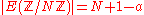 or
or 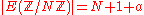
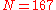 is prime using the Atkin–Morain ECPP test. First proceed through the set of 13 possible discriminants, testing whether the Legendre Symbol
is prime using the Atkin–Morain ECPP test. First proceed through the set of 13 possible discriminants, testing whether the Legendre Symbol  , and if 4N can be written as
, and if 4N can be written as 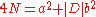 .
.
For our example D = −43 is chosen. This is because and also, using Cornacchia's algorithm, we know that
and also, using Cornacchia's algorithm, we know that 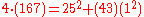 and thus a = 25 and b = 1.
and thus a = 25 and b = 1.
The next step is to calculate m. This is easily done as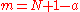 which yields
which yields 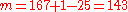 . Next we need to find a probable prime divisor of m, which was referred to as q. It must satisfy the condition that
. Next we need to find a probable prime divisor of m, which was referred to as q. It must satisfy the condition that 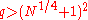
Now in this case, m = 143 = 11*13. So unfortunately we cannot choose 11 or 13 as our q, for it does not satisfy the necessary inequality. We are saved, however, by an analogous proposition to that which we stated before the Goldwasser–Kilian algorithm, which comes from a paper by Morain. It states, that given our m, we look for an s which divides m,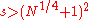 , but is not necessarily prime, and check whether, for each
, but is not necessarily prime, and check whether, for each 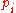 which divides s
which divides s
for some point P on our yet to be constructed curve.
If s satisfies the inequality, and its prime factors satisfy the above, then N is prime.
So in our case, we choose s = m = 143. Thus our possible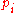 's are 11 and 13. First, it is clear that
's are 11 and 13. First, it is clear that  , and so we need only check the values of
, and so we need only check the values of
But before we can do this, we must construct our curve, and choose a point P. In order to construct the curve, we make use of complex multiplication. In our case we compute the J-invariant
Next we compute and we know our elliptic curve is of the form:
and we know our elliptic curve is of the form:
where k is as described previously and c a non-square in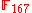 . So we can begin with
. So we can begin with
 ,
,  which yields
which yields
E:
Now, utilizing the point P = (6,6) on E it can be verified that 143P =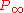 .
.
It is simple to check that 13(6, 6) = (12, 65) and 11P = (140, 147), and so, by Morain's proposition, N is prime.
of prime inputs.
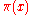 be the number of primes smaller than x
be the number of primes smaller than x
for sufficiently large x.
If one accepts this conjecture then the Goldwasser–Kilian algorithm terminates in expected polynomial time for every input. Also, if our N is of length k, then the algorithm creates a certificate of size O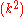 that can be verified in O
that can be verified in O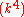 .
.
Now consider another conjecture, which will give us a bound on the total time of the algorithm.
 and
and 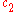 such that the amount of primes in the interval
such that the amount of primes in the interval
Then the Goldwasser Kilian algorithm proves the primality of N in an expected time of
For the Atkin–Morain algorithm, the running time stated is
O( ) for some
) for some 
. This test does not rely on elliptic curves. However we present a result where numbers of the form
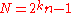 where
where 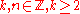 , n odd
, n odd
can be proven prime (or composite) using elliptic curves. Of course this will also provide a method for proving primality of Mersenne numbers, which correspond to the case where n = 1. It should be noted that there is a method in place for testing this form of number without elliptic curves (with a limitation on the size of k) known as the Lucas–Lehmer–Riesel test. The following method is drawn from the paper Primality Test for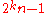 using Elliptic Curves, by Yu Tsumura.
using Elliptic Curves, by Yu Tsumura.
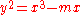 for
for 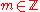 ,
,  , where
, where  is prime, and
is prime, and 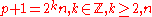 odd.
odd.
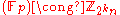 or
or
E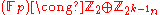
Depending on whether or not m is a quadratic residue modulo p.
 be prime, E, k, n, m as above.
be prime, E, k, n, m as above.
Take Q = (x,y) on E, x a quadratic nonresidue modulo p.
Then the order of Q is divisible by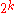 in the cyclic group
in the cyclic group
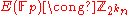 .
.
First we will present the case where n is relatively small with respect to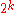 , and this will require one more theorem.
, and this will require one more theorem.
 . E, k, n, m are specified as above with the added restrictions that
. E, k, n, m are specified as above with the added restrictions that
p is a prime if and only if there exists a Q = (x,y) which is on E, such that the
 for i = 1, 2, ...,k − 1 and
for i = 1, 2, ...,k − 1 and 
where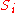 is a sequence with initial value
is a sequence with initial value 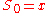
(1) Chose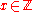 such that
such that 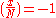 , and find y such that
, and find y such that 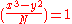
Take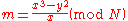
Then Q = (x,y) is on E: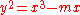 where
where 
Calculate Q = mQ. If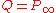 then N is composite, otherwise proceed to (2).
then N is composite, otherwise proceed to (2).
(2) Set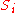 as the sequence with initial value Q. Calculate
as the sequence with initial value Q. Calculate 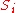 for i = 1,2,..., k − 1
for i = 1,2,..., k − 1
If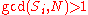 for an i, where
for an i, where  then N is composite. Otherwise, proceed to (3).
then N is composite. Otherwise, proceed to (3).
(3) If then N is prime. Otherwise, N is composite. This completes the test.
then N is prime. Otherwise, N is composite. This completes the test.
Thus, if N is prime, Q has order divisible by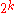 , by Theorem 3,
, by Theorem 3,
and therefore the order of Q is d | n.
d | n.
This means Q = nQ has order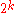 . Therefore, if (1) concludes that N is composite, it truly is composite. (2) and (3) check if Q has order
. Therefore, if (1) concludes that N is composite, it truly is composite. (2) and (3) check if Q has order 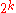 . Thus, if (2) or (3) conclude N is composite, it is composite.
. Thus, if (2) or (3) conclude N is composite, it is composite.
Now, if the algorithm concludes that N is prime, then that means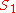 satisfies the condition of Theorem 4, and so N is truly prime.
satisfies the condition of Theorem 4, and so N is truly prime.
There is an algorithm as well for when n is large, however for this we refer to the aforementioned article.
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
primality testing techniques are among the quickest and most widely used methods in primality proving. It is an idea forwarded by Shafi Goldwasser
Shafi Goldwasser
Shafrira Goldwasser is the RSA Professor of electrical engineering and computer science at MIT, and a professor of mathematical sciences at the Weizmann Institute of Science, Israel.-Biography:...
and Joe Kilian in 1986 and turned into an algorithm by A.O.L. Atkin the same year. The algorithm was altered and improved by several collaborators subsequently, and notably by Atkin and Francois Morain, in 1993. The concept of using elliptic curves in factorization
Lenstra elliptic curve factorization
The Lenstra elliptic curve factorization or the elliptic curve factorization method is a fast, sub-exponential running time algorithm for integer factorization which employs elliptic curves. For general purpose factoring, ECM is the third-fastest known factoring method...
had been developed by H.W. Lenstra in 1985, and the implications for its use in primality testing (and proving) followed quickly.
Primality testing is a field that has been around since the time of Fermat, in whose time most algorithms were based on factoring, which become unwieldy with large input; modern algorithms treat the problems of determining whether a number is prime and what its factors are separately. It enjoys a great deal of interest with the advent of modern cryptography. Although many current tests result in a probabilistic output (N is either shown composite, or probably prime, such as with the Miller–Rabin test), the elliptic curve test, proves primality (or compositeness) with a quickly verifiable certificate.
Elliptic curve primality proving provides an alternative to (among others) the Pocklington primality test
Pocklington primality test
In mathematics, the Pocklington–Lehmer primality test is a primality test devised by Henry Cabourn Pocklington and Derrick Henry Lehmer to decide whether a given number N is prime...
, which can be difficult to implement in practice. Interestingly, the elliptic curve primality tests are based on criteria which is analogous to the Pocklington criterion, on which that test is based, where the group
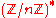 is replaced by
is replaced by 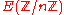 , and E is a properly chosen elliptic curve. We will now state a proposition on which to base our test, which is analogous to the Pocklington criterion, and gives rise to the Goldwasser-Kilian-Atkin form of the elliptic curve primality test.
, and E is a properly chosen elliptic curve. We will now state a proposition on which to base our test, which is analogous to the Pocklington criterion, and gives rise to the Goldwasser-Kilian-Atkin form of the elliptic curve primality test.Proposition
Let N be a positive integer, and E be the set which is defined by the equation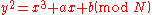 . Consider E over
. Consider E over 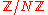 , use the usual addition law on E, and write O for the neutral element on E.
, use the usual addition law on E, and write O for the neutral element on E.Let m be an integer. If there is a prime q which divides m, and is greater than
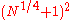 and there exists a point P on E such that
and there exists a point P on E such that(1) mP = 0
(2) (m/q)P is defined and not equal to 0
Then N is prime.
Proof
If N is composite, then there exists a prime that divides N. Define
that divides N. Define 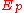 as the elliptic curve defined by the same equation as E but evaluated modulo p rather than modulo N. Define
as the elliptic curve defined by the same equation as E but evaluated modulo p rather than modulo N. Define 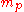 as the order of the group
as the order of the group 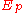 . By Hasse's theorem on elliptic curves we know
. By Hasse's theorem on elliptic curves we knowand thus
 and there exists an integer u with the property that
and there exists an integer u with the property thatLet
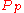 be the point P evaluated modulo p. Thus, on
be the point P evaluated modulo p. Thus, on 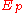 we have
we haveby (1), as
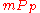 is calculated using the same method as mP, except modulo p rather than modulo N (and
is calculated using the same method as mP, except modulo p rather than modulo N (and  ).
).This contradicts (2), because if (m/q)P is defined and not equal to 0 (mod N), then the same method calculated modulo p instead of modulo N will yield
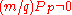
Goldwasser–Kilian algorithm
From this proposition an algorithm can be constructed to prove an integer, N, is prime. This is done as follows:Choose three integers at random, a, x, y and set
Now P = (x,y) is a point on E, where we have that E is defined by
 . Next we need an algorithm to count the number of points on E. Applied to E, this algorithm (Koblitz and others suggest Schoof's algorithm
. Next we need an algorithm to count the number of points on E. Applied to E, this algorithm (Koblitz and others suggest Schoof's algorithmSchoof's algorithm
Schoof's algorithm is an efficient algorithm to count points on elliptic curves over finite fields. The algorithm has applications in elliptic curve cryptography where it is important to know the number of points to judge the difficulty of solving the discrete logarithm problem in the group of...
) produces a number m which is the number of points on curve E over FN, provided N is prime. Next we have a criterion for deciding whether our curve E is acceptable.
If we can write m in the form
 where
where  is a small integer and q a probable prime (it has passed some previous probabilistic primality test
is a small integer and q a probable prime (it has passed some previous probabilistic primality testPrimality test
A primality test is an algorithm for determining whether an input number is prime. Amongst other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not...
, for example), then we do not discard E. If it is not possible to write m in this form, we discard our curve and randomly select another triple (a, x, y) to start over.
Assuming we find a curve which passes the criterion, proceed to calculate mP and kP. If at any stage in the calculation we encounter an undefined expression (from calculating the multiples of P or in our point counting algorithm), it gives us a non-trivial factor of N.
If
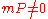 it is clear that N is not prime, because if N were prime then E would have order m, and any element of E would become 0 on multiplication by m. If kP = 0 then we have hit a dead-end and must start again with a different triple.
it is clear that N is not prime, because if N were prime then E would have order m, and any element of E would become 0 on multiplication by m. If kP = 0 then we have hit a dead-end and must start again with a different triple.Now if
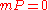 and
and 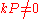 then our previous proposition tells us that N is prime. However there is one possible problem, which is the primality of q. This must be verified, using the same algorithm. So we have described a down-run procedure, where the primality of N can be proven through the primality of q and indeed smaller 'probable primes' until we have reached certain primes and are finished.
then our previous proposition tells us that N is prime. However there is one possible problem, which is the primality of q. This must be verified, using the same algorithm. So we have described a down-run procedure, where the primality of N can be proven through the primality of q and indeed smaller 'probable primes' until we have reached certain primes and are finished.Problems with the algorithm
Atkin and Morain state "the problem with GK is that Schoof's algorithm seems almost impossible to implement. It is very slow and cumbersome to count all of the points on E using Schoof's algorithm, which is the preferred algorithm for the Goldwasser–Kilian algorithm. However, the original algorithm by Schoof is not effcicient enough to provide the number of points in short time. These comments haveto be seen in the historical context, before the improvements by Elkies and Atkin to Schoof's method.
A second problem Koblitz notes is the difficulty of finding the curve E whose number of points is of the form kq, as above. There is no known theorem which guarantees we can find a suitable E in polynomially many attempts. The distribution of primes on the Hasse interval
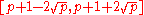 ,
,which contains m, is not the same as the distribution of primes in the group orders, counting curves with multiplity. However, this is not a significant problem in practice.
Atkin–Morain elliptic curve primality test (ECPP)
In a 1993 paper, Atkin and Morain described an algorithm ECPP which avoided the trouble of relying on a cumbersome point counting algorithm (Schoof's). The algorithm still relies on the proposition stated above, but rather than randomly generating elliptic curves and searching for a proper m, their idea was to construct a curve E where the number of points is easy to compute. Complex multiplicationComplex multiplication
In mathematics, complex multiplication is the theory of elliptic curves E that have an endomorphism ring larger than the integers; and also the theory in higher dimensions of abelian varieties A having enough endomorphisms in a certain precise sense In mathematics, complex multiplication is the...
is key in the construction of the curve.
Now, given an N for which primality needs to be proven we need to find a suitable m and q, just as in the Goldwasser-Kilian test, that will fulfill the proposition and prove the primality of N. (Of course, a point P and the curve itself, E, must also be found.)
ECPP uses complex multiplication to construct the curve E, doing so in a way that allows for m (the number of points on E) to be easily computed. We will now describe this method:
Utilization of complex multiplication requires a negative discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
, D, such that D can be written as the product of two elements
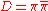 , or completely equivalently, we can write the equation:
, or completely equivalently, we can write the equation:For some a, b. If we can describe N in terms of either of these forms, we can create an elliptic curve E on
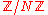 with complex multiplication (described in detail below), and the number of points is given by:
with complex multiplication (described in detail below), and the number of points is given by:For N to split into two the two elements, we need that
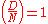 (where
(where 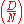 denotes the Legendre symbol
denotes the Legendre symbolLegendre symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
). This is a necessary condition, and we achieve sufficiency if the class number
Ideal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
h(D) of the order in
 is 1. This happens for only 13 values of D, which are the elements of {−3, −4, −7, −8, −11, −12, −16, −19, −27, −28, −43, −67, −163}
is 1. This happens for only 13 values of D, which are the elements of {−3, −4, −7, −8, −11, −12, −16, −19, −27, −28, −43, −67, −163}The test
Pick discriminants D in sequence of increasing h(D). For each D check if and whether 4N can be written as:
and whether 4N can be written as:This part can be verified using Cornacchia's algorithm
Cornacchia's algorithm
In computational number theory, Cornacchia's algorithm is an algorithm for solving the Diophantine equation x^2+dy^2=m, where 1\le dIn computational number theory, Cornacchia's algorithm is an algorithm for solving the Diophantine equation...
. Once acceptable D and a have been discovered, calculate
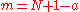 . Now if m has a prime factor q of size
. Now if m has a prime factor q of sizeuse the complex multplication method to construct the curve E and a point P on it.
Then we can use our proposition to verify the primality of N. Note that if m does not have a large prime factor or cannot be factored quickly enough, another choice of D can be made.
Complex multiplication method
For completeness, we will provide an overview of complex multiplicationComplex multiplication
In mathematics, complex multiplication is the theory of elliptic curves E that have an endomorphism ring larger than the integers; and also the theory in higher dimensions of abelian varieties A having enough endomorphisms in a certain precise sense In mathematics, complex multiplication is the...
, the way in which an elliptic curve can be created, given our D (which can be written as a product of two elements).
Assume first that
 and
and 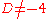 (these cases are much more easily done). It is necessary to calculate the elliptic j-invariant
(these cases are much more easily done). It is necessary to calculate the elliptic j-invariantJ-invariant
In mathematics, Klein's j-invariant, regarded as a function of a complex variable τ, is a modular function defined on the upper half-plane of complex numbers.We haveThe modular discriminant \Delta is defined as \Delta=g_2^3-27g_3^2...
s of the h(D) classes of the order of discriminant D as complex numbers. There are several formulas to calculate these.
Next create the monic polynomial
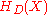 , which has roots corresponding to the h(D) values. Note, that
, which has roots corresponding to the h(D) values. Note, that 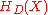 is the class polynomial. From complex multiplication theory, we know that
is the class polynomial. From complex multiplication theory, we know that 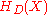 has integer coefficients, which allows us to estimate these coefficients accurately enough to discover their true values.
has integer coefficients, which allows us to estimate these coefficients accurately enough to discover their true values.Now, if N is prime, CM tells us that
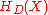 splits modulo N into a product of h(D) linear factors, based on the fact that D was chosen so that N splits as the product of two elements. Now if j is one of the h(D) roots modulo N we can define E as:
splits modulo N into a product of h(D) linear factors, based on the fact that D was chosen so that N splits as the product of two elements. Now if j is one of the h(D) roots modulo N we can define E as:c is any quadratic nonresidue mod N, and r is either 0 or 1.
Given a root j there are only two possible nonisomorphic choices of E, one for each choice of r. We have the cardinality of these curves as
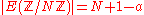 or
or 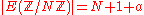
Discussion
Just as with the Goldwasser–Killian test, this one leads to a down-run procedure. Again, the culprit is q. Once we find a q that works, we must check it to be prime, so in fact we are doing the whole test now for q. Then again we may have to perform the test for factors of q. This leads to a nested certificate where at each level we have an elliptic curve E, an m and the prime in doubt, q.Example of Atkin–Morain ECPP
We construct an example to prove that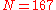 is prime using the Atkin–Morain ECPP test. First proceed through the set of 13 possible discriminants, testing whether the Legendre Symbol
is prime using the Atkin–Morain ECPP test. First proceed through the set of 13 possible discriminants, testing whether the Legendre Symbol  , and if 4N can be written as
, and if 4N can be written as 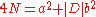 .
.For our example D = −43 is chosen. This is because
 and also, using Cornacchia's algorithm, we know that
and also, using Cornacchia's algorithm, we know that 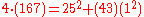 and thus a = 25 and b = 1.
and thus a = 25 and b = 1.The next step is to calculate m. This is easily done as
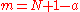 which yields
which yields 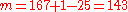 . Next we need to find a probable prime divisor of m, which was referred to as q. It must satisfy the condition that
. Next we need to find a probable prime divisor of m, which was referred to as q. It must satisfy the condition that 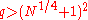
Now in this case, m = 143 = 11*13. So unfortunately we cannot choose 11 or 13 as our q, for it does not satisfy the necessary inequality. We are saved, however, by an analogous proposition to that which we stated before the Goldwasser–Kilian algorithm, which comes from a paper by Morain. It states, that given our m, we look for an s which divides m,
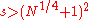 , but is not necessarily prime, and check whether, for each
, but is not necessarily prime, and check whether, for each 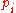 which divides s
which divides sfor some point P on our yet to be constructed curve.
If s satisfies the inequality, and its prime factors satisfy the above, then N is prime.
So in our case, we choose s = m = 143. Thus our possible
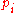 's are 11 and 13. First, it is clear that
's are 11 and 13. First, it is clear that  , and so we need only check the values of
, and so we need only check the values ofBut before we can do this, we must construct our curve, and choose a point P. In order to construct the curve, we make use of complex multiplication. In our case we compute the J-invariant
J-invariant
In mathematics, Klein's j-invariant, regarded as a function of a complex variable τ, is a modular function defined on the upper half-plane of complex numbers.We haveThe modular discriminant \Delta is defined as \Delta=g_2^3-27g_3^2...
Next we compute
 and we know our elliptic curve is of the form:
and we know our elliptic curve is of the form:-
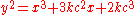 ,
,
where k is as described previously and c a non-square in
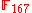 . So we can begin with
. So we can begin with ,
,  which yields
which yieldsE:

Now, utilizing the point P = (6,6) on E it can be verified that 143P =
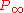 .
.It is simple to check that 13(6, 6) = (12, 65) and 11P = (140, 147), and so, by Morain's proposition, N is prime.
Complexity and running times
Goldwasser and Kilian's elliptic curve primality proving algorithm terminates in expected polynomial time for at leastof prime inputs.
Conjecture
Let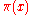 be the number of primes smaller than x
be the number of primes smaller than xfor sufficiently large x.
If one accepts this conjecture then the Goldwasser–Kilian algorithm terminates in expected polynomial time for every input. Also, if our N is of length k, then the algorithm creates a certificate of size O
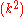 that can be verified in O
that can be verified in O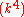 .
.Now consider another conjecture, which will give us a bound on the total time of the algorithm.
Conjecture 2
Suppose there exist positive constants and
and 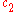 such that the amount of primes in the interval
such that the amount of primes in the interval-
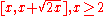 is larger than
is larger than 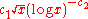
Then the Goldwasser Kilian algorithm proves the primality of N in an expected time of
For the Atkin–Morain algorithm, the running time stated is
O(
 ) for some
) for some 
Primes of special form
For some forms of numbers, it is possible to find 'short-cuts' to a primality proof. This is the case for the Mersenne numbers. In fact, due to their special structure, which allows for easier verification of primality, the largest known prime number is a Mersenne number. There has been a method in use for some time to verify primality of Mersenne numbers, known as the Lucas–Lehmer testLucas–Lehmer test
In computational number theory, the Lucas test is a primality test for a natural number n; it requires that the prime factors of n − 1 be already known. It is the basis of the Pratt certificate that gives a concise verification that n is prime....
. This test does not rely on elliptic curves. However we present a result where numbers of the form
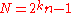 where
where 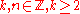 , n odd
, n oddcan be proven prime (or composite) using elliptic curves. Of course this will also provide a method for proving primality of Mersenne numbers, which correspond to the case where n = 1. It should be noted that there is a method in place for testing this form of number without elliptic curves (with a limitation on the size of k) known as the Lucas–Lehmer–Riesel test. The following method is drawn from the paper Primality Test for
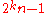 using Elliptic Curves, by Yu Tsumura.
using Elliptic Curves, by Yu Tsumura.Group structure of E(FN)
We take E as our elliptic curve, where E is of the form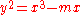 for
for 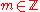 ,
,  , where
, where  is prime, and
is prime, and 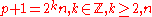 odd.
odd.Theorem 2
E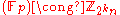 or
orE
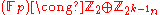
Depending on whether or not m is a quadratic residue modulo p.
Theorem 3
Let be prime, E, k, n, m as above.
be prime, E, k, n, m as above.Take Q = (x,y) on E, x a quadratic nonresidue modulo p.
Then the order of Q is divisible by
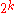 in the cyclic group
in the cyclic group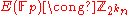 .
.First we will present the case where n is relatively small with respect to
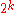 , and this will require one more theorem.
, and this will require one more theorem.Theorem 4
Choose a . E, k, n, m are specified as above with the added restrictions that
. E, k, n, m are specified as above with the added restrictions that-
 and
and 
p is a prime if and only if there exists a Q = (x,y) which is on E, such that the
 for i = 1, 2, ...,k − 1 and
for i = 1, 2, ...,k − 1 and 
where
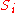 is a sequence with initial value
is a sequence with initial value 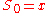
The algorithm
We provide the following algorithm, which relies mainly on Theorems 3 and 4. To verify the primality of a given number N, perform the following steps:(1) Chose
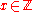 such that
such that 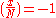 , and find y such that
, and find y such that 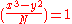
Take
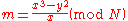
Then Q = (x,y) is on E:
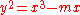 where
where 
Calculate Q = mQ. If
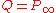 then N is composite, otherwise proceed to (2).
then N is composite, otherwise proceed to (2).(2) Set
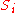 as the sequence with initial value Q. Calculate
as the sequence with initial value Q. Calculate 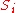 for i = 1,2,..., k − 1
for i = 1,2,..., k − 1If
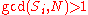 for an i, where
for an i, where  then N is composite. Otherwise, proceed to (3).
then N is composite. Otherwise, proceed to (3).(3) If
 then N is prime. Otherwise, N is composite. This completes the test.
then N is prime. Otherwise, N is composite. This completes the test.Justification of the algorithm
In (1), and elliptic curve, E is picked, along with a point Q on E, such that the x-coordinate of Q is a quadratic nonresidue. We can sayThus, if N is prime, Q has order divisible by
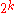 , by Theorem 3,
, by Theorem 3, and therefore the order of Q is
 d | n.
d | n.This means Q = nQ has order
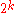 . Therefore, if (1) concludes that N is composite, it truly is composite. (2) and (3) check if Q has order
. Therefore, if (1) concludes that N is composite, it truly is composite. (2) and (3) check if Q has order 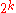 . Thus, if (2) or (3) conclude N is composite, it is composite.
. Thus, if (2) or (3) conclude N is composite, it is composite.Now, if the algorithm concludes that N is prime, then that means
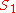 satisfies the condition of Theorem 4, and so N is truly prime.
satisfies the condition of Theorem 4, and so N is truly prime.There is an algorithm as well for when n is large, however for this we refer to the aforementioned article.