
Electron localization function
Encyclopedia
In quantum chemistry
, the electron localization function (ELF) is a measure of the likelihood of finding an electron
in the neighborhood space of a reference electron located at a given point and with the same spin. Physically, this measures the extent of spatial localization of the reference electron and provides a method for the mapping of electron pair
probability in multielectronic systems.
ELF's usefulness stems from the manner it allows the analysis of electron localization in a chemically intuitive way. For example, the shell structure of heavy atoms is obvious when plotting ELF against the radial distance from the nucleus; the ELF for radon, for example, has six clear maxima, whereas the electronic density
decreases monotonically and the radially weighted density fails to show all shells. When applied to molecules, an analysis of the ELF shows a clear separation between the core and valence electron, and also shows covalent bond
s and lone pair
s, in what has been called "a faithful visualization of VSEPR theory
in action". Another feature of the ELF is that it is invariant with respect to transformation of the molecular orbital
s.
The ELF was originally defined by Axel D. Becke
and K. E. Edgecombe in 1990. They first argued that a measure of the electron localization is provided by

where ρ is the electron spin density and τ the kinetic energy density. D is expected to be small in those regions of space where localized electrons are to be found. Given the arbitrariness of the magnitude of the localization measure provided by D, it is compared to the corresponding value for a uniform electron gas with spin density equal to ρ(r), which is given by

The ratio,
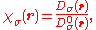
is a dimensionless localization index that expresses electron localization with respect to the uniform electron gas. In the final step, the ELF is defined in terms of χ by mapping its values on to the range 0 ≤ ELF ≤ 1 by defining the electron localization function as
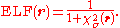
ELF = 1 corresponding to perfect localization and ELF = ½ corresponding to the electron gas.
The original derivation was based on Hartree-Fock
theory. For density functional theory
, the approach was generalized by Savin in 1992.
The approach of electron localization (not in this form) was pioneered by Bader. Bader's analysis partitions the charge density in a molecule to "atoms" according to zero-flux surfaces (surfaces across which no electron flow is taking place). Bader's analysis allows many properties such as multipole moments, energies and forces, to be partitioned in a defensible and consistent manner to individual atoms within molecules.
Both the Bader approach, and the ELF approach to partitioning of molecular properties have gained popularity in recent years, because the fastest, accurate ab-initio calculations of molecular properties are now mostly made using density functional theory (DFT), which directly calculates the electron density. This electron density is the property whose properties are then analyzed using with Bader charge analysis or Electron Localization Functions. One of the most popular functionals in DFT was first proposed by Becke, who also originated Electron Localization Functions.
Quantum chemistry
Quantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...
, the electron localization function (ELF) is a measure of the likelihood of finding an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
in the neighborhood space of a reference electron located at a given point and with the same spin. Physically, this measures the extent of spatial localization of the reference electron and provides a method for the mapping of electron pair
Electron pair
In chemistry, an electron pair consists of two electrons that occupy the same orbital but have opposite spins.Because electrons are fermions, the Pauli exclusion principle forbids these particles from having exactly the same quantum numbers. Therefore the only way to occupy the same orbital, i.e....
probability in multielectronic systems.
ELF's usefulness stems from the manner it allows the analysis of electron localization in a chemically intuitive way. For example, the shell structure of heavy atoms is obvious when plotting ELF against the radial distance from the nucleus; the ELF for radon, for example, has six clear maxima, whereas the electronic density
Electronic density
In quantum mechanics, and in particular quantum chemistry, the electronic density is a measure of the probability of an electron occupying an infinitesimal element of space surrounding any given point. It is a scalar quantity depending upon three spatial variables and is typically denoted as either...
decreases monotonically and the radially weighted density fails to show all shells. When applied to molecules, an analysis of the ELF shows a clear separation between the core and valence electron, and also shows covalent bond
Covalent bond
A covalent bond is a form of chemical bonding that is characterized by the sharing of pairs of electrons between atoms. The stable balance of attractive and repulsive forces between atoms when they share electrons is known as covalent bonding....
s and lone pair
Lone pair
In chemistry, a lone pair is a valence electron pair without bonding or sharing with other atoms. They are found in the outermost electron shell of an atom, so lone pairs are a subset of a molecule's valence electrons...
s, in what has been called "a faithful visualization of VSEPR theory
VSEPR theory
Valence shell electron pair repulsion theory is a model in chemistry used to predict the shape of individual molecules based upon the extent of electron-pair electrostatic repulsion. It is also named Gillespie–Nyholm theory after its two main developers...
in action". Another feature of the ELF is that it is invariant with respect to transformation of the molecular orbital
Molecular orbital
In chemistry, a molecular orbital is a mathematical function describing the wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The term "orbital" was first...
s.
The ELF was originally defined by Axel D. Becke
Axel D. Becke
Axel Dieter Becke is a physical chemist and Professor of Chemistry at Dalhousie University, Canada. He is a leading researcher in the application of density functional theory to molecules.- Early life :...
and K. E. Edgecombe in 1990. They first argued that a measure of the electron localization is provided by

where ρ is the electron spin density and τ the kinetic energy density. D is expected to be small in those regions of space where localized electrons are to be found. Given the arbitrariness of the magnitude of the localization measure provided by D, it is compared to the corresponding value for a uniform electron gas with spin density equal to ρ(r), which is given by

The ratio,
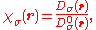
is a dimensionless localization index that expresses electron localization with respect to the uniform electron gas. In the final step, the ELF is defined in terms of χ by mapping its values on to the range 0 ≤ ELF ≤ 1 by defining the electron localization function as
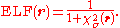
ELF = 1 corresponding to perfect localization and ELF = ½ corresponding to the electron gas.
The original derivation was based on Hartree-Fock
Hartree-Fock
In computational physics and chemistry, the Hartree–Fock method is an approximate method for the determination of the ground-state wave function and ground-state energy of a quantum many-body system....
theory. For density functional theory
Density functional theory
Density functional theory is a quantum mechanical modelling method used in physics and chemistry to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. With this theory, the properties of a many-electron system can be determined by...
, the approach was generalized by Savin in 1992.
The approach of electron localization (not in this form) was pioneered by Bader. Bader's analysis partitions the charge density in a molecule to "atoms" according to zero-flux surfaces (surfaces across which no electron flow is taking place). Bader's analysis allows many properties such as multipole moments, energies and forces, to be partitioned in a defensible and consistent manner to individual atoms within molecules.
Both the Bader approach, and the ELF approach to partitioning of molecular properties have gained popularity in recent years, because the fastest, accurate ab-initio calculations of molecular properties are now mostly made using density functional theory (DFT), which directly calculates the electron density. This electron density is the property whose properties are then analyzed using with Bader charge analysis or Electron Localization Functions. One of the most popular functionals in DFT was first proposed by Becke, who also originated Electron Localization Functions.
External links
- Frank R. Wagner (ed.) Electron localizability: chemical bonding analysis in direct and momentum space. Max-Planck-Institut für Chemische Physik fester Stoffe, 2002. (accessed 2008-09-02).

