Eisenbud–Levine–Khimshiashvili signature formula
Encyclopedia
In mathematics, and especially differential topology
and singularity theory
, the Eisenbud–Levine–Khimshiashvili signature formula gives a way of computing the Poincaré-Hopf index of a real, analytic
vector field
at an algebraicially isolated singularity. It is named after David Eisenbud
, Harold Levine
, and George Khimshiashvili. Intuitively, the index of a vector field near a zero is the number of times the vector field wraps around the sphere. Because analytic vector fields have a rich algebraic structure, the techniques of commutative algebra
can be brought to bear to compute their index. The signature formula expresses the index of an analytic vector field in terms of the signature of a certain quadratic form
.
, and write x for a point in Rn, where
Let X be a vector field
on Rn. For there exist function
s such that one may express X as
To say that X is an analytic vector field means that each of the functions is an analytic function
. One says that X is singular at a point p in Rn (or that p is a singular point of X) if , i.e. X vanishes at p. In terms of the functions it means that for all . A singular point p of X is called isolated (or that p is an isolated singularity of X) if and there exists an open neighbourhood , containing p, such that for all q in U, different from p. An isolated singularity of X is called algebraically isolated if, when considered over the complex domain, it remains isolated.
Since the Poincaré-Hopf index at a point is a purely local invariant (cf. Poincaré-Hopf theorem), one may restrict one's study to that of germs
. Assume that each of the ƒk from above are function germs, i.e. In turn, one may call X at vector field germ.
of analytic function germs . Assume that X is a vector field germ of the form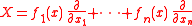
with an algebraicially isolated singularity at 0. Where, as mentioned above, each of the ƒk are function germs . Denote by IX the ideal
generated by the ƒk, i.e. Then one considers the local algebra, BX, given by the quotient
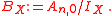
The Eisenbud–Levine–Khimshiashvili signature formula gives the index of the vector field X, at 0, by assigning a non-degenerate bilinear form on the local algebra BX. The signature of this non-degenerate bilinear form being equal to the index of X.
The dimension of BX is finite if and only if the complexification
of X has an isolated singularity at 0 in Cn; i.e. X has an algebraically isolated singularity at 0 in Rn. In this case, BX will be a finite dimensional, real algebra.
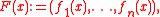
for all . Let denote the determinant
of the Jacobian matrix of F with respect to the basis
Finally, let denote the equivalence class of JF, modulo
IX. Using ∗ to denote multiplication in BX one is able to define a non-degenerate bilinear form β as follows: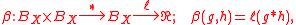
where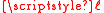
is any linear function such that
As mentioned: the signature of β is exactly the signature of X at 0.
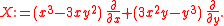
Clearly X has an algebraically isolated singularity at 0 since if and only if The ideal IX is given by and
The first step for finding the non-degenerate, bilinear form β is to calculate the multiplication table of BX; reducing each entry modulo IX. Whence
Direct calculation shows that , and so Next one assigns values for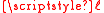
. One may take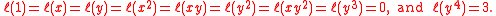
This choice was made so that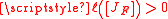
as was required by the hypothesis, and to make the calculations involve integers, as aposed to fractions. Applying this to the multiplication table gives the matrix representation of the bilinear form β with respect to the given basis:
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
and singularity theory
Singularity theory
-The notion of singularity:In mathematics, singularity theory is the study of the failure of manifold structure. A loop of string can serve as an example of a one-dimensional manifold, if one neglects its width. What is meant by a singularity can be seen by dropping it on the floor...
, the Eisenbud–Levine–Khimshiashvili signature formula gives a way of computing the Poincaré-Hopf index of a real, analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
at an algebraicially isolated singularity. It is named after David Eisenbud
David Eisenbud
David Eisenbud is an American mathematician. He is a professor of mathematics at the University of California, Berkeley and was Director of the Mathematical Sciences Research Institute from 1997 to 2007....
, Harold Levine
Harold Levine
Harold Levine is an American mathematician who is professor emeritus at Stanford university. He specializes in wave motion and optics. In 1954, he was awarded a Guggenheim fellowship.-External links:...
, and George Khimshiashvili. Intuitively, the index of a vector field near a zero is the number of times the vector field wraps around the sphere. Because analytic vector fields have a rich algebraic structure, the techniques of commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
can be brought to bear to compute their index. The signature formula expresses the index of an analytic vector field in terms of the signature of a certain quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
.
Nomenclature
Consider the n-dimensional space Rn. Assume that Rn has some fixed coordinate systemCoordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
, and write x for a point in Rn, where
Let X be a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
on Rn. For there exist function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s such that one may express X as
To say that X is an analytic vector field means that each of the functions is an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
. One says that X is singular at a point p in Rn (or that p is a singular point of X) if , i.e. X vanishes at p. In terms of the functions it means that for all . A singular point p of X is called isolated (or that p is an isolated singularity of X) if and there exists an open neighbourhood , containing p, such that for all q in U, different from p. An isolated singularity of X is called algebraically isolated if, when considered over the complex domain, it remains isolated.
Since the Poincaré-Hopf index at a point is a purely local invariant (cf. Poincaré-Hopf theorem), one may restrict one's study to that of germs
Germ (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
. Assume that each of the ƒk from above are function germs, i.e. In turn, one may call X at vector field germ.
Construction
Let An,0 denote the ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of analytic function germs . Assume that X is a vector field germ of the form
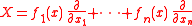
with an algebraicially isolated singularity at 0. Where, as mentioned above, each of the ƒk are function germs . Denote by IX the ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
generated by the ƒk, i.e. Then one considers the local algebra, BX, given by the quotient
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
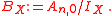
The Eisenbud–Levine–Khimshiashvili signature formula gives the index of the vector field X, at 0, by assigning a non-degenerate bilinear form on the local algebra BX. The signature of this non-degenerate bilinear form being equal to the index of X.
The dimension of BX is finite if and only if the complexification
Complexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
of X has an isolated singularity at 0 in Cn; i.e. X has an algebraically isolated singularity at 0 in Rn. In this case, BX will be a finite dimensional, real algebra.
Definition of the bilinear form
Using the analytic components of X, one defines another analytic germ given by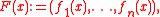for all . Let denote the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the Jacobian matrix of F with respect to the basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
Finally, let denote the equivalence class of JF, modulo
Modulo
In the mathematical community, the word modulo is often used informally. Generally, to say "A is the same as B modulo C" means, more-or-less, "A and B are the same except for differences accounted for or explained by C"....
IX. Using ∗ to denote multiplication in BX one is able to define a non-degenerate bilinear form β as follows:
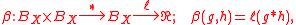
where
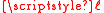is any linear function such thatAs mentioned: the signature of β is exactly the signature of X at 0.
Example
Consider the case of a vector field on the plane. Consider the case where X is given by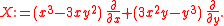Clearly X has an algebraically isolated singularity at 0 since if and only if The ideal IX is given by and
The first step for finding the non-degenerate, bilinear form β is to calculate the multiplication table of BX; reducing each entry modulo IX. Whence
Direct calculation shows that , and so Next one assigns values for
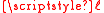. One may take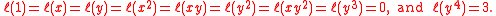This choice was made so that
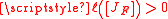as was required by the hypothesis, and to make the calculations involve integers, as aposed to fractions. Applying this to the multiplication table gives the matrix representation of the bilinear form β with respect to the given basis:
The eigenvalues of this matrix are There are 3 negative eigenvalues , and six positive eigenvalues ; meaning that the signature of β is . It follows that X has Poincaré-Hopf index +3 at the origin.
Topological verification
With this particular choice of X it is possible to verify the Poincaré-Hopf index is +3 by a direct application of the definition of Poincaré-Hopf index. This is very rarely the case, and was the reason for the choice of example. If one takes polar coordinates on the plane, i.e. and then and Restrict X to a circle, centre 0, radius , denoted by C0,ε; and consider the map given by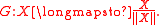
The Poincaré-Hopf index of X is, by definition, the topological degree of the map G. Restricting X to the circle C0,ε, for arbitrarily small ε, gives
meaning that as θ makes one rotation about the circle C0,ε in an anti-clockwise direction; the image G(θ) makes three complete, anti-clockwise rotations about the unit circle C0,1. Meaning that the topological degree of G is +3 and that the Poincaré-Hopf index of X at 0 is +3.