Einstein radius
Encyclopedia
The Einstein radius is the radius of an Einstein ring
, and is a characteristic angle for gravitational lens
ing in general, as typical distances between images in gravitational lensing are of the order of the Einstein radius.
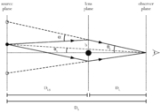
 In the following derivation of the Einstein radius, we will assume that all of mass
In the following derivation of the Einstein radius, we will assume that all of mass  of the lensing galaxy
of the lensing galaxy 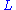 is concentrated in the center of the galaxy.
is concentrated in the center of the galaxy.
For a point mass the deflection can be calculated and is one of the classical tests of general relativity
. For small angles the total deflection by a point mass
the total deflection by a point mass  is given (see Schwarzschild metric
is given (see Schwarzschild metric
) by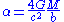
where
By noting that, for small angles and with the angle expressed in radian
s, the point of nearest approach b at an angle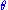 for the lens
for the lens  on a distance
on a distance 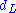 is given by
is given by 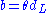 , we can re-express the bending angle
, we can re-express the bending angle  as
as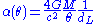 (eq. 1)
(eq. 1)
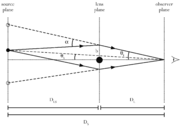
If we set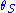 as the angle at which one would see the source without the lens (which is generally not observable), and
as the angle at which one would see the source without the lens (which is generally not observable), and 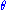 as the observed angle of the image of the source with respect to the lens, then one can see from the geometry of lensing (counting distances in the source plane) that the vertical distance spanned by the angle
as the observed angle of the image of the source with respect to the lens, then one can see from the geometry of lensing (counting distances in the source plane) that the vertical distance spanned by the angle 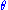 at a distance
at a distance 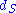 is the same as the sum of the two vertical distances
is the same as the sum of the two vertical distances 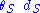 plus
plus 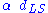 . This gives the lens equation,
. This gives the lens equation,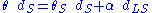 ,
,
which can be rearranged to give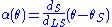 (eq. 2)
(eq. 2)
By setting (eq. 1) equal to (eq. 2), and rearranging, we get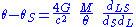
For a source right behind the lens,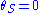 , and the lens equation for a point mass gives a characteristic value for
, and the lens equation for a point mass gives a characteristic value for 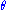 that is called the Einstein radius, denoted
that is called the Einstein radius, denoted 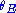 . Putting
. Putting 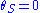 and solving for
and solving for 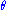 gives
gives
The Einstein radius for a point mass provides a convenient linear scale to make dimensionless lensing variables. In terms of the Einstein radius, the lens equation for a point mass becomes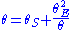
Substituting for the constants gives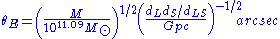
In the latter form, the mass is expressed in solar mass
es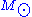 and the distances in Gigaparsec
and the distances in Gigaparsec
(Gpc). The Einstein radius most prominent for a lens typically halfway between the source and the observer.
For a dense cluster with mass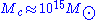 at a distance of 1 Gigaparsec (1 Gpc) this radius could be as large as 100 arcsec (called macrolensing). For a Gravitational microlensing
at a distance of 1 Gigaparsec (1 Gpc) this radius could be as large as 100 arcsec (called macrolensing). For a Gravitational microlensing
event (with masses of order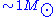 ) search for at galactic distances (say
) search for at galactic distances (say 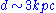 ), the typical Einstein radius would be of order milli-arcseconds. Consequently separate images in microlensing events are impossible to observe with current techniques.
), the typical Einstein radius would be of order milli-arcseconds. Consequently separate images in microlensing events are impossible to observe with current techniques.
The argument above can be extended for lenses which have a distributed mass, rather than a point mass, by using a different expression for the bend angle . The positions
. The positions 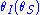 of the images can then be calculated. For small deflections this mapping is one-to-one and consists of distortions of the observed positions which are invertible. This is called weak lensing. For large deflections one can have multiple images and a non-invertible mapping: this is called strong lensing. Note that in order for a distributed mass to result in an Einstein ring, it must be axially symmetric.
of the images can then be calculated. For small deflections this mapping is one-to-one and consists of distortions of the observed positions which are invertible. This is called weak lensing. For large deflections one can have multiple images and a non-invertible mapping: this is called strong lensing. Note that in order for a distributed mass to result in an Einstein ring, it must be axially symmetric.
Einstein ring
In observational astronomy an Einstein ring is the deformation of the light from a source into a ring through gravitational lensing of the source's light by an object with an extremely large mass . This occurs when the source, lens and observer are all aligned...
, and is a characteristic angle for gravitational lens
Gravitational lens
A gravitational lens refers to a distribution of matter between a distant source and an observer, that is capable of bending the light from the source, as it travels towards the observer...
ing in general, as typical distances between images in gravitational lensing are of the order of the Einstein radius.
Derivation

 of the lensing galaxy
of the lensing galaxy 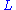 is concentrated in the center of the galaxy.
is concentrated in the center of the galaxy.For a point mass the deflection can be calculated and is one of the classical tests of general relativity
Tests of general relativity
At its introduction in 1915, the general theory of relativity did not have a solid empirical foundation. It was known that it correctly accounted for the "anomalous" precession of the perihelion of Mercury and on philosophical grounds it was considered satisfying that it was able to unify Newton's...
. For small angles
 the total deflection by a point mass
the total deflection by a point mass  is given (see Schwarzschild metric
is given (see Schwarzschild metricSchwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
) by
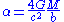
where
-
 is the impact parameterImpact parameterThe impact parameter b is defined as the perpendicular distance between the path of a projectile and the center of the field U created by an object that the projectile is approaching...
is the impact parameterImpact parameterThe impact parameter b is defined as the perpendicular distance between the path of a projectile and the center of the field U created by an object that the projectile is approaching...
(the distance of nearest approach of the lightbeam to the center of mass) -
 is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
, -
 is the speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
is the speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
.
By noting that, for small angles and with the angle expressed in radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s, the point of nearest approach b at an angle
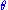 for the lens
for the lens  on a distance
on a distance 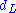 is given by
is given by 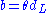 , we can re-express the bending angle
, we can re-express the bending angle  as
as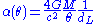 (eq. 1)
(eq. 1)If we set
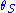 as the angle at which one would see the source without the lens (which is generally not observable), and
as the angle at which one would see the source without the lens (which is generally not observable), and 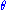 as the observed angle of the image of the source with respect to the lens, then one can see from the geometry of lensing (counting distances in the source plane) that the vertical distance spanned by the angle
as the observed angle of the image of the source with respect to the lens, then one can see from the geometry of lensing (counting distances in the source plane) that the vertical distance spanned by the angle 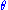 at a distance
at a distance 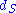 is the same as the sum of the two vertical distances
is the same as the sum of the two vertical distances 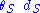 plus
plus 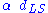 . This gives the lens equation,
. This gives the lens equation,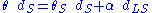 ,
,which can be rearranged to give
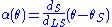 (eq. 2)
(eq. 2)By setting (eq. 1) equal to (eq. 2), and rearranging, we get
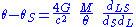
For a source right behind the lens,
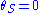 , and the lens equation for a point mass gives a characteristic value for
, and the lens equation for a point mass gives a characteristic value for 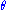 that is called the Einstein radius, denoted
that is called the Einstein radius, denoted 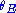 . Putting
. Putting 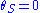 and solving for
and solving for 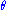 gives
gives
The Einstein radius for a point mass provides a convenient linear scale to make dimensionless lensing variables. In terms of the Einstein radius, the lens equation for a point mass becomes
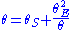
Substituting for the constants gives
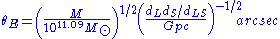
In the latter form, the mass is expressed in solar mass
Solar mass
The solar mass , , is a standard unit of mass in astronomy, used to indicate the masses of other stars and galaxies...
es
 and the distances in Gigaparsec
and the distances in GigaparsecParsec
The parsec is a unit of length used in astronomy. It is about 3.26 light-years, or just under 31 trillion kilometres ....
(Gpc). The Einstein radius most prominent for a lens typically halfway between the source and the observer.
For a dense cluster with mass
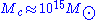 at a distance of 1 Gigaparsec (1 Gpc) this radius could be as large as 100 arcsec (called macrolensing). For a Gravitational microlensing
at a distance of 1 Gigaparsec (1 Gpc) this radius could be as large as 100 arcsec (called macrolensing). For a Gravitational microlensingGravitational microlensing
Gravitational microlensing is an astronomical phenomenon due to the gravitational lens effect. It can be used to detect objects ranging from the mass of a planet to the mass of a star, regardless of the light they emit. Typically, astronomers can only detect bright objects that emit lots of light ...
event (with masses of order
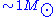 ) search for at galactic distances (say
) search for at galactic distances (say 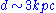 ), the typical Einstein radius would be of order milli-arcseconds. Consequently separate images in microlensing events are impossible to observe with current techniques.
), the typical Einstein radius would be of order milli-arcseconds. Consequently separate images in microlensing events are impossible to observe with current techniques.The argument above can be extended for lenses which have a distributed mass, rather than a point mass, by using a different expression for the bend angle
 . The positions
. The positions 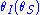 of the images can then be calculated. For small deflections this mapping is one-to-one and consists of distortions of the observed positions which are invertible. This is called weak lensing. For large deflections one can have multiple images and a non-invertible mapping: this is called strong lensing. Note that in order for a distributed mass to result in an Einstein ring, it must be axially symmetric.
of the images can then be calculated. For small deflections this mapping is one-to-one and consists of distortions of the observed positions which are invertible. This is called weak lensing. For large deflections one can have multiple images and a non-invertible mapping: this is called strong lensing. Note that in order for a distributed mass to result in an Einstein ring, it must be axially symmetric.

