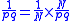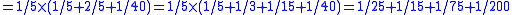Egyptian Mathematical Leather Roll
Encyclopedia
The Egyptian Mathematical Leather Roll (EMLR) was a 10 × 17 in (25 × 43 cm) leather roll purchased by Alexander Henry Rhind
in 1858. It was sent to the British Museum
in 1864, along with the Rhind Mathematical Papyrus
, but the former was not chemically softened and unrolled until 1927 (Scott, Hall 1927).
The writing consists of Middle Kingdom
hieratic
characters written right to left. Scholars date the EMLR to the 17th century BCE.
Of the 26 rational numbers listed, ten are Eye of Horus
numbers: 1/2, 1/4 (twice), 1/8 (thrice), 1/16 (twice), 1/32, 1/64 converted to Egyptian fractions. There are seven other even rational numbers converted to Egyptian fractions: 1/6 (listed twice–but wrong once), 1/10, 1/12, 1/14, 1/20 and 1/30. Finally, there were nine odd rational numbers converted to Egyptian fractions: 2/3, 1/3 (twice), 1/5, 1/7, 1/9, 1/11, 1/13 and 1/15, training patterns for scribal students to learn the RMP 2/n table method.
The British Museum examiners found no introduction or description to how or why the equivalent unit fraction series were computed. Equivalent unit fraction series are associated with fractions 1/3, 1/4, 1/8 and 1/16. There was a trivial error associated with the final 1/15 unit fraction series. The 1/15 series was listed as equal to 1/6. Another serious error was associated with 1/13, an issue that the 1927 examiners did not attempt to resolve.
and the Lahun Mathematical Papyri
. Both types of tables were used to aid in computations dealing with fractions, and for the conversion of measuring units.
It has been noted that there are groups of unit fraction decompositions in the EMLR which are very similar. For instance lines 5 and 6 easily combine into the equation 1/3 + 1/6 = 1/2. It is easy to derive lines 11, 13, 24, 20, 21, 19, 23, 22, 25 and 26 by dividing this equation by 3, 4, 5, 6, 7, 8, 10, 15, 16 and 32 respectively.
Some of the problems would lend themselves to a solution via an algorithm which involves multiplying both the numerator and the denominator by the same term and then further reducing the resulting equation:
This method leads to a solution for the fraction 1/8 as appears in the EMLR when using N=25 (using modern mathematical notation):
Other:
Alexander Henry Rhind
Alexander Henry Rhind was a Scottish lawyer and Egyptologist.Born in Wick on 26 July 1833 in the Highlands, Rhind studied at the University of Edinburgh...
in 1858. It was sent to the British Museum
British Museum
The British Museum is a museum of human history and culture in London. Its collections, which number more than seven million objects, are amongst the largest and most comprehensive in the world and originate from all continents, illustrating and documenting the story of human culture from its...
in 1864, along with the Rhind Mathematical Papyrus
Rhind Mathematical Papyrus
The Rhind Mathematical Papyrus , is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 BC...
, but the former was not chemically softened and unrolled until 1927 (Scott, Hall 1927).
The writing consists of Middle Kingdom
Middle Kingdom of Egypt
The Middle Kingdom of Egypt is the period in the history of ancient Egypt stretching from the establishment of the Eleventh Dynasty to the end of the Fourteenth Dynasty, between 2055 BC and 1650 BC, although some writers include the Thirteenth and Fourteenth dynasties in the Second Intermediate...
hieratic
Hieratic
Hieratic refers to a cursive writing system that was used in the provenance of the pharaohs in Egypt and Nubia that developed alongside the hieroglyphic system, to which it is intimately related...
characters written right to left. Scholars date the EMLR to the 17th century BCE.
Mathematical content
This leather roll is an aid for computing Egyptian fractions. It contains 26 sums of unit fractions which equal another unit fraction. The sums appear in two columns, and are followed by two more columns which contain exactly the same sums.| Column 1 | |Column 2 | |Column 3 | |Column 4 |
|---|---|---|---|
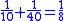 |
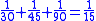 |
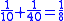 |
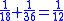 |
 |
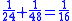 |
 |
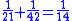 |
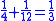 |
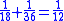 |
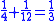 |
 |
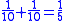 |
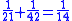 |
 |
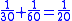 |
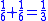 |
 |
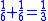 |
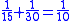 |
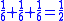 |
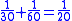 |
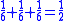 |
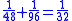 |
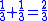 |
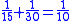 |
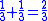 |
 |
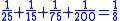 |
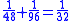 |
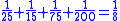 |
|
 |
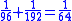 |
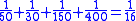 |
|
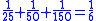 |
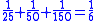 |
||
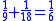 |
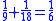 |
||
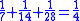 |
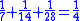 |
||
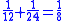 |
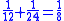 |
||
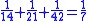 |
 |
||
 |
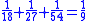 |
||
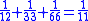 |
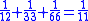 |
||
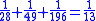 |
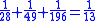 |
||
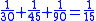 |
|||
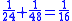 |
Of the 26 rational numbers listed, ten are Eye of Horus
Eye of Horus
The Eye of Horus is an ancient Egyptian symbol of protection, royal power and good health. The eye is personified in the goddess Wadjet...
numbers: 1/2, 1/4 (twice), 1/8 (thrice), 1/16 (twice), 1/32, 1/64 converted to Egyptian fractions. There are seven other even rational numbers converted to Egyptian fractions: 1/6 (listed twice–but wrong once), 1/10, 1/12, 1/14, 1/20 and 1/30. Finally, there were nine odd rational numbers converted to Egyptian fractions: 2/3, 1/3 (twice), 1/5, 1/7, 1/9, 1/11, 1/13 and 1/15, training patterns for scribal students to learn the RMP 2/n table method.
The British Museum examiners found no introduction or description to how or why the equivalent unit fraction series were computed. Equivalent unit fraction series are associated with fractions 1/3, 1/4, 1/8 and 1/16. There was a trivial error associated with the final 1/15 unit fraction series. The 1/15 series was listed as equal to 1/6. Another serious error was associated with 1/13, an issue that the 1927 examiners did not attempt to resolve.
Modern analysis
The original mathematical texts never explain where the procedures and formulas came from. This holds true for the EMLR as well. Scholars have attempted to deduce what techniques the ancient Egyptians may have used to construct both the unit fraction tables of the EMLR and the 2 /n tables known from the Rhind Mathematical PapyrusRhind Mathematical Papyrus
The Rhind Mathematical Papyrus , is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 BC...
and the Lahun Mathematical Papyri
Lahun Mathematical Papyri
The Lahun Mathematical Papyri are part of a collection of Kahun Papyri discovered at El-Lahun by Flinders Petrie during excavations of a worker's town near the pyramid of Sesostris II...
. Both types of tables were used to aid in computations dealing with fractions, and for the conversion of measuring units.
It has been noted that there are groups of unit fraction decompositions in the EMLR which are very similar. For instance lines 5 and 6 easily combine into the equation 1/3 + 1/6 = 1/2. It is easy to derive lines 11, 13, 24, 20, 21, 19, 23, 22, 25 and 26 by dividing this equation by 3, 4, 5, 6, 7, 8, 10, 15, 16 and 32 respectively.
Some of the problems would lend themselves to a solution via an algorithm which involves multiplying both the numerator and the denominator by the same term and then further reducing the resulting equation:
This method leads to a solution for the fraction 1/8 as appears in the EMLR when using N=25 (using modern mathematical notation):
Modern conclusions
The EMLR has been considered a student scribe test document since 1927, the year that the text was unrolled at the British Museum. The scribe practiced conversions of rational numbers 1/p and 1/pq to alternative unit fraction series. Reading available Middle Kingdom math records, RMP 2/n table being one, modern students of Egyptian arithmetic may see that trained scribes improved conversions of 2/n and n/p to concise unit fraction series by applying algorithmic and non-algorithmic methods.Chronology
The following chronology shows several milestones that marked the recent progress toward reporting a clearer understanding of the EMLR's contents, related to the RMP 2/n table.- 1895 – Hultsch suggested that all RMP 2/p series were coded by aliquot parts.
- 1927 – Glanville concluded that EMLR arithmetic was purely additive.
- 1929 – Vogel reported the EMLR to be more important (than the RMP), though it contains only 25 unit fraction series.
- 1950 – Bruins independently confirms Hultsch’s RMP 2/p analysis (Bruins 1950)
- 1972 – Gillings found solutions to an easier RMP problem, the 2/pq series (Gillings 1972: 95–96).
- 1982 – Knorr identifies RMP unit fractions 2/35, 2/91 and 2/95 as exceptions to the 2/pq problem.
- 2002 – Gardner identifies five abstract EMLR patterns.
See also
Egyptian mathematical texts:- Moscow Mathematical PapyrusMoscow Mathematical PapyrusThe Moscow Mathematical Papyrus is an ancient Egyptian mathematical papyrus, also called the Golenishchev Mathematical Papyrus, after its first owner, Egyptologist Vladimir Golenishchev. Golenishchev bought the papyrus in 1892 or 1893 in Thebes...
- Lahun Mathematical PapyriLahun Mathematical PapyriThe Lahun Mathematical Papyri are part of a collection of Kahun Papyri discovered at El-Lahun by Flinders Petrie during excavations of a worker's town near the pyramid of Sesostris II...
- Berlin papyrusBerlin papyrusThe Berlin Papyrus 6619, commonly known as the Berlin Papyrus, is an ancient Egyptian papyrus document from the Middle Kingdom. This papyrus was found at the ancient burial ground of Saqqara in the early 19th century CE....
- Akhmim Wooden TabletAkhmim wooden tabletThe Akhmim wooden tablets or Cairo wooden tablets are two ancient Egyptian wooden writing tablets. They each measure about 18 by 10 inches and are covered with plaster. The tablets are inscribed on both sides. The inscriptions on the first tablet includes a list of servants, which is followed...
- Reisner PapyrusReisner PapyrusThe Reisner Papyri date to the reign of Senusret I, who was king of Ancient Egypt in the 19th century BCE. The documents were discovered by Dr. G.A. Reisner during excavations in 1901-04 in Naga ed-Deir in southern Egypt. A total of four papyrusrolls were found in a wooden coffin in a tomb. * The...
- Rhind Mathematical PapyrusRhind Mathematical PapyrusThe Rhind Mathematical Papyrus , is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 BC...
Other:
- Liber AbaciLiber AbaciLiber Abaci is a historic book on arithmetic by Leonardo of Pisa, known later by his nickname Fibonacci...
- Sylvia Couchoud
Further reading
- Brown, Kevin S. The Akhmin Papyrus 1995 – Egyptian Unit Fractions 1995
- Bruckheimer, Maxim and Y. Salomon. “Some Comments on R. J. Gillings’ Analysis of the 2/n Table in the Rhind Papyrus.” Historia Mathematica 4 Berlin (1977): 445–452.
- Bruins, Evert M. “Platon et la table égyptienne 2/n”. Janus 46, Amsterdam, (1957): 253–263.
- Bruins, Evert M. “Egyptian Arithmetic.” Janus 68, Amsterdam, (1981): 33–52.
- Bruins, Evert M. “Reducible and Trivial Decompositions Concerning Egyptian Arithmetics”. Janus 68, Amsterdam, (1981): 281–297.
- Daressy, Georges. “Akhmim Wood Tablets”, Le Caire Imprimerie de l’Institut Francais d’Archeologie Orientale, 1901, 95–96.
- Gardner, Milo. "Mathematical Roll of Egypt", Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures, Springer, Nov. 2005.
- Gillings, Richard J. “The Egyptian Mathematical Leather Roll”. Australian Journal of Science 24 (1962): 339–344, Mathematics in the Time of the Pharaohs. Cambridge, Mass.: MIT Press, 1972. New York: Dover, reprint 1982.
- Gillings, Richard J. “The Recto of the Rhind Mathematical Papyrus: How Did the Ancient Egyptian Scribe Prepare It ?” Archive for History of Exact Sciences 12 (1974), 291–298.
- Gillings, Richard J. “The Recto of the RMP and the EMLR”, Historia Mathematica, Toronto 6 (1979), 442–447.
- Gillings, Richard J. “The Egyptian Mathematical Leather Role–Line 8. How Did the Scribe Do it?” (Historia Mathematica 1981), 456–457.
- Gunn, Battiscombe George. Review of ”The Rhind Mathematical Papyrus” by T. E. Peet. The Journal of Egyptian Archaeology 12 London, (1926): 123–137.
- Imhausen, Annette. “Egyptian Mathematical Texts and their Contexts”, Science in Context, vol 16, Cambridge (UK), (2003): 367–389.
- Legon, John A.R. “A Kahun Mathematical Fragment”. Discussions in Egyptology, 24 Oxford, (1992).
- Lüneburg, H. “Zerlgung von Bruchen in Stammbruche” Leonardi Pisani Liber Abbaci oder Lesevergnügen eines Mathematikers, Wissenschaftsverlag, Mannheim, 1993. 81–85.
- Rees, C. S. “Egyptian Fractions”, Mathematical Chronicle 10, Auckland, (1981): 13–33.
- Roero, C. S. “Egyptian mathematics” Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences” I. Grattan-Guinness (ed), London, (1994): 30–45.
- Scott, A. and Hall, H.R., “Laboratory Notes: Egyptian Mathematical Leather Roll of the Seventeenth Century BC”, British Museum Quarterly, Vol 2, London, (1927): 56.
- Sylvester, J. J. “On a Point in the Theory of Vulgar Fractions”: American Journal Of Mathematics, 3 Baltimore (1880): 332–335, 388–389.