Lahun Mathematical Papyri
Encyclopedia
The Lahun Mathematical Papyri (also known as the Kahun Mathematical Papyri) are part of a collection of Kahun Papyri discovered at El-Lahun
(also known as Lahun, Kahun or Il-Lahun) by Flinders Petrie during excavations of a worker's town near the pyramid of Sesostris II. The Kahun Papyrus
are a collection of texts including administrative texts, medical texts, veterinarian texts and six fragments devoted to mathematics.
The mathematical texts most commented on are usually named:
reports an odd n table up to 101. These fraction tables were related to multiplication problems and the use of unit fractions, namely n/p scaled by LCM m to mn/mp. With the exception of 2/3, all fractions were represented as sums of unit fractions (i.e. of the form 1/n), first in red numbers. Multiplication algorithms and scaling factors involved repeated doubling of numbers, and other operations. Doubling a unit fraction with an even denominator was simple, divided the denominator by 2. Doubling a fraction with an odd denominator however results in a fraction of the form 2/n. The RMP 2/n table and RMP 36 rules allowed scribes to find decompositions of 2/n into unit fractions for specific needs, most often to solve otherwise un-scalable rational numbers (i.e. 28/97 in RMP 31,and 30/53 n RMP 36 by substituting 26/97 + 2/97 and 28/53 + 2/53) and generally n/p by (n - 2)/p + 2/p. Decompositions were unique. Red auxiliary numbers
selected divisors of denominators mp that best summed to numerator mn.
El-Lahun
Located in the Faiyum, Egypt, el-Lahun or Kahun is the workers' village associated with the pyramid of Senusret II . It is located near the modern village of el-Lahun , and is often known by that name...
(also known as Lahun, Kahun or Il-Lahun) by Flinders Petrie during excavations of a worker's town near the pyramid of Sesostris II. The Kahun Papyrus
Kahun Papyrus
The Kahun Papyri are a collection of ancient Egyptian texts discussing administrative, mathematical and medical topics. Its many fragments were discovered by Flinders Petrie in 1889 and are kept at the University College London. This collection of papyri is one of the largest ever found. Most of...
are a collection of texts including administrative texts, medical texts, veterinarian texts and six fragments devoted to mathematics.
The mathematical texts most commented on are usually named:
- Lahun IV.2 (or Kahun IV.2) (UC 32159): This fragment contains a tableMathematical tableBefore calculators were cheap and plentiful, people would use mathematical tables —lists of numbers showing the results of calculation with varying arguments— to simplify and drastically speed up computation...
of Egyptian fraction representations of numbers of the form 2/n. A more complete version of this table of fractions is given in the Rhind Mathematical PapyrusRhind Mathematical PapyrusThe Rhind Mathematical Papyrus , is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 BC...
. - Lahun IV.3 (or Kahun IV.3) (UC 32160) contains numbers in arithmetical progression and a problem very much like problem 40 of the Rhind Mathematical Papyrus. Another problem on this fragment computes the volume of a cylindrical granary. In this problem the scribe uses a formula which takes measurements in cubits and computes the volume and expresses it in terms of the unit khar. Given the diameter (d) and height (h) of the cylindrical granary:
.
- In modern mathematical notation this is equal to
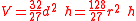(measured in khar). - This problem resembles problem 42 of the Rhind Mathematical PapyrusRhind Mathematical PapyrusThe Rhind Mathematical Papyrus , is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 BC...
. The formula is equivalent to
measured in cubic-cubits as used in the other problems.
- Lahun XLV.1 (or Kahun XLV.1) (UC 32161) contains a group of very large numbers (hundreds of thousands).
- Lahun LV.3 (or Kahun LV.3) (UC 32134A and UC 32134B) contains a so called aha problem which asks one to solve for a certain quantity. The problem resembles ones from the Rhind Mathematical Papyrus (problems 24-29).
- Lahun LV.4 (or Kahun LV.4) (UC 32162) contains what seems to be an area computation and a problem concerning the value of ducks, geese and cranes. The problem concerning fowl is a baku problem and most closely resembles problem 69 in the Rhind Mathematical PapyrusRhind Mathematical PapyrusThe Rhind Mathematical Papyrus , is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 BC...
and problems 11 and 21 in the Moscow Mathematical PapyrusMoscow Mathematical PapyrusThe Moscow Mathematical Papyrus is an ancient Egyptian mathematical papyrus, also called the Golenishchev Mathematical Papyrus, after its first owner, Egyptologist Vladimir Golenishchev. Golenishchev bought the papyrus in 1892 or 1893 in Thebes...
.
- Unnamed fragment (UC 32118B). This is a fragmentary piece.
The 2/n tables
The Lahun papyrus IV.2 reports a 2/n table for odd n, n = 1, , 21. The Rhind Mathematical PapyrusRhind Mathematical Papyrus
The Rhind Mathematical Papyrus , is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 BC...
reports an odd n table up to 101. These fraction tables were related to multiplication problems and the use of unit fractions, namely n/p scaled by LCM m to mn/mp. With the exception of 2/3, all fractions were represented as sums of unit fractions (i.e. of the form 1/n), first in red numbers. Multiplication algorithms and scaling factors involved repeated doubling of numbers, and other operations. Doubling a unit fraction with an even denominator was simple, divided the denominator by 2. Doubling a fraction with an odd denominator however results in a fraction of the form 2/n. The RMP 2/n table and RMP 36 rules allowed scribes to find decompositions of 2/n into unit fractions for specific needs, most often to solve otherwise un-scalable rational numbers (i.e. 28/97 in RMP 31,and 30/53 n RMP 36 by substituting 26/97 + 2/97 and 28/53 + 2/53) and generally n/p by (n - 2)/p + 2/p. Decompositions were unique. Red auxiliary numbers
Red auxiliary numbers
In the study of ancient Egyptian mathematics, red auxiliary numbers were additive numbers that summed to a numerator used in Middle Kingdom arithmetic problems. In the 1650 BCE Rhind Mathematical Papyrus , the additive set of divisors were written in red ink...
selected divisors of denominators mp that best summed to numerator mn.
External links
- John Legon: A Kahun Mathematical Fragment
- http://ahmespapyrus.blogspot.com/2009/01/ahmes-papyrus-new-and-old.html
- Math-History-List
- MathOrigins.com
- History of Egyptian fractions
- Medical Papyrus, UCL website
- The Kahun Gynaecological Papyrus