EWMA chart
Encyclopedia
In statistical quality control
, the EWMA chart (or exponentially-weighted moving average chart) is a type of control chart
used to monitor either variables or attributes-type data using the monitored business
or industrial process's entire history of output. While other control charts treat rational subgroups of samples individually, the EWMA chart tracks the exponentially-weighted moving average of all prior sample means. EWMA weights samples in geometrically decreasing order so that the most recent samples are weighted most highly while the most distant samples contribute very little.
Although the normal distribution is the basis of the EWMA chart, the chart is also relatively robust in the face of non-normally distributed quality characteristics. There is, however, an adaptation of the chart accounts for quality characteristics that are better modeled by the Poisson distribution
. The chart monitors only the process mean; monitoring the process variability requires the use of some other technique.
The EWMA control chart requires a knowledgeable person to select two parameters before setup:
Instead of plotting rational subgroup averages directly, the EWMA chart computes successive observations zi by computing the rational subgroup average,
, and then combining that new subgroup average with the running average of all preceding observations, zi - 1, using the specially–chosen weight, λ, as follows:
.
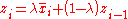The control limits for this chart type are
where T and S are the estimates of the long-term process mean and standard deviation established during control-chart setup and n is the number of samples in the rational subgroup. Note that the limits widen for each successive rational subgroup, approaching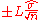 
.
The EWMA chart is sensitive to small shifts in the process mean, but does not match the ability of Shewhart-style charts (namely the
and R and 
and s charts) to detect larger shifts. One author recommends superimposing the EWMA chart on top of a suitable Shewhart-style chart with widened control limits in order to detect both small and large shifts in the process mean.
Statistical process control
Statistical process control is the application of statistical methods to the monitoring and control of a process to ensure that it operates at its full potential to produce conforming product. Under SPC, a process behaves predictably to produce as much conforming product as possible with the least...
, the EWMA chart (or exponentially-weighted moving average chart) is a type of control chart
Control chart
Control charts, also known as Shewhart charts or process-behaviour charts, in statistical process control are tools used to determine whether or not a manufacturing or business process is in a state of statistical control.- Overview :...
used to monitor either variables or attributes-type data using the monitored business
Business process
A business process or business method is a collection of related, structured activities or tasks that produce a specific service or product for a particular customer or customers...
or industrial process's entire history of output. While other control charts treat rational subgroups of samples individually, the EWMA chart tracks the exponentially-weighted moving average of all prior sample means. EWMA weights samples in geometrically decreasing order so that the most recent samples are weighted most highly while the most distant samples contribute very little.
Although the normal distribution is the basis of the EWMA chart, the chart is also relatively robust in the face of non-normally distributed quality characteristics. There is, however, an adaptation of the chart accounts for quality characteristics that are better modeled by the Poisson distribution
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
. The chart monitors only the process mean; monitoring the process variability requires the use of some other technique.
The EWMA control chart requires a knowledgeable person to select two parameters before setup:
- The first parameter is λ, the weight given to the most recent rational subgroup mean. λ must satisfy 0 < λ ≤ 1, but selecting the "right" value is a matter of personal preference and experience. One source recommends 0.05 ≤ λ ≤ 0.25, while another recommends 0.2 ≤ λ ≤ 0.3.
- The second parameter is L, the multiple of the rational subgroup standard deviation that establishes the control limits. L is typically set at 3 to match other control charts, but it may be necessary to reduce L slightly for small values of λ.
Instead of plotting rational subgroup averages directly, the EWMA chart computes successive observations zi by computing the rational subgroup average,
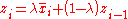, and then combining that new subgroup average with the running average of all preceding observations, zi - 1, using the specially–chosen weight, λ, as follows:.The control limits for this chart type are
where T and S are the estimates of the long-term process mean and standard deviation established during control-chart setup and n is the number of samples in the rational subgroup. Note that the limits widen for each successive rational subgroup, approaching 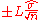.The EWMA chart is sensitive to small shifts in the process mean, but does not match the ability of Shewhart-style charts (namely the
and R and and s charts) to detect larger shifts. One author recommends superimposing the EWMA chart on top of a suitable Shewhart-style chart with widened control limits in order to detect both small and large shifts in the process mean.