
Durbin test
Encyclopedia
In the analysis of designed experiments, the Friedman test
is the most common non-parametric test for complete block designs. The Durbin test is a nonparametric test for balanced incomplete designs that reduces to the Friedman test in the case of a complete block design.
, k treatments are applied to b blocks. In a complete block design, every treatment is run for every block and the data are arranged as follows:
For some experiments, it may not be realistic to run all treatments in all blocks, so one may need to run an incomplete block design. In this case, it is strongly recommended to run a balanced incomplete design. A balanced incomplete block design has the following properties:
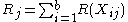
The Durbin test is then
The test statistic is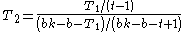
where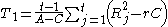
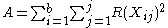

where t is the number of treatments, k is the number of treatments per block, b is the number of blocks, and r is the number of times each treatment appears.
For significance level α, the critical region is given by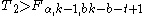
where Fα, k − 1, bk − b − t + 1 denotes the α-quantile
of the F distribution with k − 1 numerator degrees of freedom and bk − b − t + 1 denominator degrees of freedom. The null hypothesis is rejected if the test statistic is in the critical region. If the hypothesis of identical treatment effects is rejected, it is often desirable to determine which treatments are different (i.e., multiple comparisons
). Treatments i and j are considered different if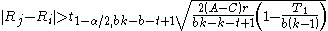
where Rj and Ri are the column sum of ranks within the blocks, t1 − α/2, bk − b − t + 1 denotes the 1 − α/2 quantile of the t distribution
with bk − b − t + 1 degrees of freedom.
, which would have an approximate null distribution of χt − 12 (that is, chi-squared with t − 1 degrees of freedom). The T2 statistic has slightly more accurate critical regions, so it is now the preferred statistic. The T2 statistic is the two-way analysis of variance statistic computed on the ranks R(Xij).
Friedman test
The Friedman test is a non-parametric statistical test developed by the U.S. economist Milton Friedman. Similar to the parametric repeated measures ANOVA, it is used to detect differences in treatments across multiple test attempts. The procedure involves ranking each row together, then...
is the most common non-parametric test for complete block designs. The Durbin test is a nonparametric test for balanced incomplete designs that reduces to the Friedman test in the case of a complete block design.
Background
In a randomized block designRandomized block design
In the statistical theory of the design of experiments, blocking is the arranging of experimental units in groups that are similar to one another. Typically, a blocking factor is a source of variability that is not of primary interest to the experimenter...
, k treatments are applied to b blocks. In a complete block design, every treatment is run for every block and the data are arranged as follows:
| Treatment 1 | Treatment 2 |  |
Treatment k | |
|---|---|---|---|---|
| Block 1 | X11 | X12 |  |
X1k |
| Block 2 | X21 | X22 |  |
X2k |
| Block 3 | X31 | X32 |  |
X3k |
 |
 |
 |
 |
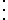 |
| Block b | Xb1 | Xb2 |  |
Xbk |
For some experiments, it may not be realistic to run all treatments in all blocks, so one may need to run an incomplete block design. In this case, it is strongly recommended to run a balanced incomplete design. A balanced incomplete block design has the following properties:
- Every block contains k experimental units.
- Every treatment appears in r blocks.
- Every treatment appears with every other treatment an equal number of times.
Test assumptions
The Durbin test is based on the following assumptions:- The b blocks are mutually independent. That means the results within one block do not affect the results within other blocks.
- The data can be meaningfully ranked (i.e., the data have at least an ordinal scale).
Test definition
Let R(Xij) be the rank assigned to Xij within block i (i.e., ranks within a given row). Average ranks are used in the case of ties. The ranks are summed to obtain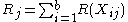
The Durbin test is then
- H0: The treatment effects have identical effects
- Ha: At least one treatment is different from at least one other treatment
The test statistic is
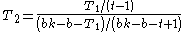
where
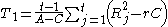
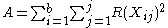

where t is the number of treatments, k is the number of treatments per block, b is the number of blocks, and r is the number of times each treatment appears.
For significance level α, the critical region is given by
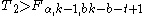
where Fα, k − 1, bk − b − t + 1 denotes the α-quantile
Quantile function
In probability and statistics, the quantile function of the probability distribution of a random variable specifies, for a given probability, the value which the random variable will be at, or below, with that probability...
of the F distribution with k − 1 numerator degrees of freedom and bk − b − t + 1 denominator degrees of freedom. The null hypothesis is rejected if the test statistic is in the critical region. If the hypothesis of identical treatment effects is rejected, it is often desirable to determine which treatments are different (i.e., multiple comparisons
Multiple comparisons
In statistics, the multiple comparisons or multiple testing problem occurs when one considers a set of statistical inferences simultaneously. Errors in inference, including confidence intervals that fail to include their corresponding population parameters or hypothesis tests that incorrectly...
). Treatments i and j are considered different if
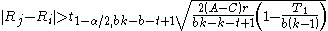
where Rj and Ri are the column sum of ranks within the blocks, t1 − α/2, bk − b − t + 1 denotes the 1 − α/2 quantile of the t distribution
T distribution
The phrase "T distribution" may refer to* Student's t-test in univariate statistics,* Student's t-distribution in univariate probability theory,* Hotelling's T-square distribution in multivariate statistics.* Multivariate Student distribution....
with bk − b − t + 1 degrees of freedom.
Historical note
T1 was the original statistic proposed by James DurbinJames Durbin
James Durbin is a British statistician and econometrician, known particularly for his work on time series analysis and serial correlation.He was educated at St John's College, Cambridge where his contemporaries included David Cox and Denis Sargan...
, which would have an approximate null distribution of χt − 12 (that is, chi-squared with t − 1 degrees of freedom). The T2 statistic has slightly more accurate critical regions, so it is now the preferred statistic. The T2 statistic is the two-way analysis of variance statistic computed on the ranks R(Xij).
Related tests
Cochran's Q test is applied for the special case of a binary response variable (i.e., one that can have only one of two possible outcomes).See also
- Analysis of varianceAnalysis of varianceIn statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
- Friedman testFriedman testThe Friedman test is a non-parametric statistical test developed by the U.S. economist Milton Friedman. Similar to the parametric repeated measures ANOVA, it is used to detect differences in treatments across multiple test attempts. The procedure involves ranking each row together, then...
- Kruskal-Wallis one-way analysis of varianceKruskal-Wallis one-way analysis of varianceIn statistics, the Kruskal–Wallis one-way analysis of variance by ranks is a non-parametric method for testing whether samples originate from the same distribution. The factual null hypothesis is that the populations from which the samples originate, have the same median...
- Van der Waerden testVan der Waerden testNamed for the Dutch mathematician Bartel Leendert van der Waerden, the Van der Waerden test is a statistical test that k population distribution functions are equal. The Van Der Waerden test converts the ranks from a standard Kruskal-Wallis one-way analysis of variance to quantiles of the standard...
- robust ANOVA

