
Van der Waerden test
Encyclopedia
Named for the Dutch mathematician Bartel Leendert van der Waerden
, the Van der Waerden test is a statistical test that k population distribution functions are equal. The Van Der Waerden test converts the ranks from a standard Kruskal-Wallis one-way analysis of variance
to quantile
s of the standard normal distribution (details given below). These are called normal scores and the test is computed from these normal scores.
The k population version of the test is an extension of the test for two populations published by Van der Waerden (1952,1953).
(ANOVA) is a data analysis
technique for examining the significance of the factors (independent variables) in a multi-factor model. The one factor model can be thought of as a generalization of the two sample t-test. That is, the two sample t-test is a test of the hypothesis that two population means are equal. The one factor ANOVA tests the hypothesis that k population means are equal. The standard ANOVA assumes that the errors (i.e., residuals) are normally distributed. If this normality assumption is not valid, an alternative is to use a non-parametric test.
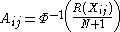
where R(Xij) denotes the rank of observation Xij and where Φ-1 denotes the normal quantile function
. The average of the normal scores for each sample can then be computed as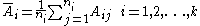
The variance of the normal scores can be computed as
The Van Der Waerden test can then be defined as follows:
The test statistic is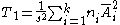
For significance level α, the critical region is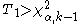
where Χα,k − 12 is the α-quantile
of the chi-squared distribution with k − 1 degrees of freedom. The null hypothesis is rejected if the test statistic is in the critical region. If the hypothesis of identical distributions is rejected, one can perform a multiple comparisons
procedure to determine which pairs of populations tend to differ. The populations i and j seem to be different if the following inequality is satisfied:
with t1 − α/2 the (1 − α/2)-quantile
of the t distribution
.
. The Kruskal-Wallis test is based on the ranks of the data. The advantage of the Van Der Waerden test is that it provides the high efficiency of the standard ANOVA analysis when the normality assumptions are in fact satisfied, but it also provides the robustness of the Kruskal-Wallis test when the normality assumptions are not satisfied.
Bartel Leendert van der Waerden
Bartel Leendert van der Waerden was a Dutch mathematician and historian of mathematics....
, the Van der Waerden test is a statistical test that k population distribution functions are equal. The Van Der Waerden test converts the ranks from a standard Kruskal-Wallis one-way analysis of variance
Kruskal-Wallis one-way analysis of variance
In statistics, the Kruskal–Wallis one-way analysis of variance by ranks is a non-parametric method for testing whether samples originate from the same distribution. The factual null hypothesis is that the populations from which the samples originate, have the same median...
to quantile
Quantile
Quantiles are points taken at regular intervals from the cumulative distribution function of a random variable. Dividing ordered data into q essentially equal-sized data subsets is the motivation for q-quantiles; the quantiles are the data values marking the boundaries between consecutive subsets...
s of the standard normal distribution (details given below). These are called normal scores and the test is computed from these normal scores.
The k population version of the test is an extension of the test for two populations published by Van der Waerden (1952,1953).
Background
Analysis of VarianceAnalysis of variance
In statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
(ANOVA) is a data analysis
Data analysis
Analysis of data is a process of inspecting, cleaning, transforming, and modeling data with the goal of highlighting useful information, suggesting conclusions, and supporting decision making...
technique for examining the significance of the factors (independent variables) in a multi-factor model. The one factor model can be thought of as a generalization of the two sample t-test. That is, the two sample t-test is a test of the hypothesis that two population means are equal. The one factor ANOVA tests the hypothesis that k population means are equal. The standard ANOVA assumes that the errors (i.e., residuals) are normally distributed. If this normality assumption is not valid, an alternative is to use a non-parametric test.
Test definition
Let ni (i = 1, 2, ..., k) represent the sample sizes for each of the k groups (i.e., samples) in the data. Let N denote the sample size for all groups. Let Xij represent the ith value in the jth group. The normal scores are computed as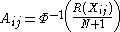
where R(Xij) denotes the rank of observation Xij and where Φ-1 denotes the normal quantile function
Quantile function
In probability and statistics, the quantile function of the probability distribution of a random variable specifies, for a given probability, the value which the random variable will be at, or below, with that probability...
. The average of the normal scores for each sample can then be computed as
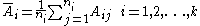
The variance of the normal scores can be computed as

The Van Der Waerden test can then be defined as follows:
- H0: All of the k population distribution functions are identical
- Ha: At least one of the populations tends to yield larger observations than at least one of the other populations
The test statistic is
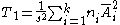
For significance level α, the critical region is
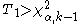
where Χα,k − 12 is the α-quantile
Quantile
Quantiles are points taken at regular intervals from the cumulative distribution function of a random variable. Dividing ordered data into q essentially equal-sized data subsets is the motivation for q-quantiles; the quantiles are the data values marking the boundaries between consecutive subsets...
of the chi-squared distribution with k − 1 degrees of freedom. The null hypothesis is rejected if the test statistic is in the critical region. If the hypothesis of identical distributions is rejected, one can perform a multiple comparisons
Multiple comparisons
In statistics, the multiple comparisons or multiple testing problem occurs when one considers a set of statistical inferences simultaneously. Errors in inference, including confidence intervals that fail to include their corresponding population parameters or hypothesis tests that incorrectly...
procedure to determine which pairs of populations tend to differ. The populations i and j seem to be different if the following inequality is satisfied:

with t1 − α/2 the (1 − α/2)-quantile
Quantile
Quantiles are points taken at regular intervals from the cumulative distribution function of a random variable. Dividing ordered data into q essentially equal-sized data subsets is the motivation for q-quantiles; the quantiles are the data values marking the boundaries between consecutive subsets...
of the t distribution
T distribution
The phrase "T distribution" may refer to* Student's t-test in univariate statistics,* Student's t-distribution in univariate probability theory,* Hotelling's T-square distribution in multivariate statistics.* Multivariate Student distribution....
.
Comparison with the Kruskal-Wallis test
The most common non-parametric test for the one-factor model is the Kruskal-Wallis testKruskal-Wallis one-way analysis of variance
In statistics, the Kruskal–Wallis one-way analysis of variance by ranks is a non-parametric method for testing whether samples originate from the same distribution. The factual null hypothesis is that the populations from which the samples originate, have the same median...
. The Kruskal-Wallis test is based on the ranks of the data. The advantage of the Van Der Waerden test is that it provides the high efficiency of the standard ANOVA analysis when the normality assumptions are in fact satisfied, but it also provides the robustness of the Kruskal-Wallis test when the normality assumptions are not satisfied.

