
Dowker space
Encyclopedia
A Dowker space is a topological space
that is T4
but not countably paracompact
.
(a T4 space), then the following are equivalent:
Dowker conjectured that there were no Dowker spaces, and the conjecture was not resolved until M.E. Rudin
constructed one in 1971. Rudin's counterexample is a very large space (of cardinality ) and is generally not well-behaved
) and is generally not well-behaved
. Zoltán Balogh
gave the first ZFC construction of a small (cardinality continuum
) example, which was more well-behaved
than Rudin's. Using PCF theory
, M. Kojman and S. Shelah
constructed a Dowker space of cardinality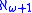 .
.
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
that is T4
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
but not countably paracompact
Paracompact space
In mathematics, a paracompact space is a topological space in which every open cover admits a locally finite open refinement. Paracompact spaces are sometimes also required to be Hausdorff. Paracompact spaces were introduced by ....
.
Equivalences
If X is a normal T1 spaceT1 space
In topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
(a T4 space), then the following are equivalent:
- X is a Dowker space
- The product of X with the unit interval is not normal. C. H. DowkerClifford Hugh DowkerClifford Hugh Dowker was a topologist known for his work in point-set topology and also for his contributions in category theory, sheaf theory and knot theory.-Biography:...
1951 - X is not countably metacompactMetacompact spaceIn mathematics, in the field of general topology, a topological space is said to be metacompact if every open cover has a point finite open refinement...
. This was also shown by Dowker, according to Balogh.
Dowker conjectured that there were no Dowker spaces, and the conjecture was not resolved until M.E. Rudin
Mary Ellen Rudin
Mary Ellen Rudin is an American mathematician.Born Mary Ellen Estill, she attended the University of Texas, completing her B.A. in 1944 and her Ph.D. in 1949, under Robert Lee Moore. In 1953, she married the mathematician Walter Rudin. Following her mentor Moore, her research centers on point-set...
constructed one in 1971. Rudin's counterexample is a very large space (of cardinality
 ) and is generally not well-behaved
) and is generally not well-behavedWell-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
. Zoltán Balogh
Zoltán Tibor Balogh
Zoltán "Zoli" Tibor Balogh was a Hungarian-born mathematician, specializing in set-theoretic topology. His father, Tibor Balogh, was also a mathematician. His best known work concerned solutions to problems involving normality of products, most notably the first ZFC construction of a small ...
gave the first ZFC construction of a small (cardinality continuum
Cardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
) example, which was more well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
than Rudin's. Using PCF theory
PCF theory
PCF theory is the name of a mathematical theory, introduced by Saharon , that deals with the cofinality of the ultraproducts of ordered sets. It gives strong upper bounds on the cardinalities of power sets of singular cardinals, and has many more applications as well...
, M. Kojman and S. Shelah
Saharon Shelah
Saharon Shelah is an Israeli mathematician. He is a professor of mathematics at the Hebrew University of Jerusalem and Rutgers University in New Jersey.-Biography:...
constructed a Dowker space of cardinality
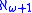 .
.

