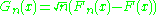Donsker's theorem
Encyclopedia
In probability theory
, Donsker's theorem, named after M. D. Donsker
, identifies a certain stochastic process
as a limit of empirical process
es. It is sometimes called the functional central limit theorem.
A centered and scaled version of empirical distribution function
Fn defines an empirical process
indexed by x ∈ R.
Theorem (Donsker, Skorokhod, Kolmogorov) The sequence of Gn(x), as random elements of the Skorokhod space
, converges in distribution to a Gaussian process
G with zero mean and covariance given by
The process G(x) can be written as B(F(x)) where B is a standard Brownian bridge
on the unit interval.
, for fixed x, the random variable Gn(x) converges in distribution to a Gaussian (normal) random variable
G(x) with zero mean and variance F(x)(1 − F(x)) as the sample size n grows.
Kolmogorov (1933) showed that when F is continuous
, the supremum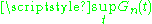
and supremum of absolute value, 
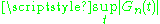converges in distribution to the laws of the same functionals of the Brownian bridge
B(t), see the Kolmogorov–Smirnov test. In 1949 Doob asked whether the convergence in distribution held for more general functionals, thus formulating a problem of weak convergence of random functions in a suitable function space
.
In 1952 Donsker stated and proved (not quite correctly) a general extension for the Doob-Kolmogorov heuristic approach. In the original paper, Donsker proved that the convergence in law of Gn to the Brownian bridge holds for Uniform[0,1
] distributions with respect to uniform convergence in t over the interval [0,1].
However Donsker's formulation was not quite correct because of the problem of measurability of the functionals of discontinuous processes. In 1956 Skorokhod and Kolmogorov defined a separable metric d, called the Skorokhod metric, on the space of cadlag functions on [0,1], such that convergence for d to a continuous function is equivalent to convergence for the sup norm, and showed that Gn converges in law in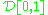
to the Brownian bridge.
Later Dudley reformulated Donsker's result to avoid the problem of measurability and the need of the Skorokhod metric. One can prove that there exist Xi, iid uniform in [0,1] and a sequence of sample-continuous Brownian bridges Bn, such that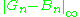
is measurable and converges in probability to 0. An improved version of this result, providing more detail on the rate of convergence, is the Komlós–Major–Tusnády approximation
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, Donsker's theorem, named after M. D. Donsker
M. D. Donsker
Monroe David Donsker was an American mathematician and a professor of mathematics at New York University . His research interest was in the field of probability theory....
, identifies a certain stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
as a limit of empirical process
Empirical process
The study of empirical processes is a branch of mathematical statistics and a sub-area of probability theory. It is a generalization of the central limit theorem for empirical measures...
es. It is sometimes called the functional central limit theorem.
A centered and scaled version of empirical distribution function
Empirical distribution function
In statistics, the empirical distribution function, or empirical cdf, is the cumulative distribution function associated with the empirical measure of the sample. This cdf is a step function that jumps up by 1/n at each of the n data points. The empirical distribution function estimates the true...
Fn defines an empirical process
Empirical process
The study of empirical processes is a branch of mathematical statistics and a sub-area of probability theory. It is a generalization of the central limit theorem for empirical measures...
indexed by x ∈ R.
Theorem (Donsker, Skorokhod, Kolmogorov) The sequence of Gn(x), as random elements of the Skorokhod space
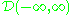, converges in distribution to a Gaussian processGaussian process
In probability theory and statistics, a Gaussian process is a stochastic process whose realisations consist of random values associated with every point in a range of times such that each such random variable has a normal distribution...
G with zero mean and covariance given by
The process G(x) can be written as B(F(x)) where B is a standard Brownian bridge
Brownian bridge
A Brownian bridge is a continuous-time stochastic process B whose probability distribution is the conditional probability distribution of a Wiener process W given the condition that B = B = 0.The expected value of the bridge is zero, with variance t, implying that the most...
on the unit interval.
History
By the classical central limit theoremCentral limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
, for fixed x, the random variable Gn(x) converges in distribution to a Gaussian (normal) random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
G(x) with zero mean and variance F(x)(1 − F(x)) as the sample size n grows.
Kolmogorov (1933) showed that when F is continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, the supremum
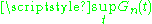and supremum of absolute value, 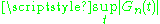converges in distribution to the laws of the same functionals of the Brownian bridgeBrownian bridge
A Brownian bridge is a continuous-time stochastic process B whose probability distribution is the conditional probability distribution of a Wiener process W given the condition that B = B = 0.The expected value of the bridge is zero, with variance t, implying that the most...
B(t), see the Kolmogorov–Smirnov test. In 1949 Doob asked whether the convergence in distribution held for more general functionals, thus formulating a problem of weak convergence of random functions in a suitable function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
.
In 1952 Donsker stated and proved (not quite correctly) a general extension for the Doob-Kolmogorov heuristic approach. In the original paper, Donsker proved that the convergence in law of Gn to the Brownian bridge holds for Uniform[0,1
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
] distributions with respect to uniform convergence in t over the interval [0,1].
However Donsker's formulation was not quite correct because of the problem of measurability of the functionals of discontinuous processes. In 1956 Skorokhod and Kolmogorov defined a separable metric d, called the Skorokhod metric, on the space of cadlag functions on [0,1], such that convergence for d to a continuous function is equivalent to convergence for the sup norm, and showed that Gn converges in law in
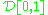to the Brownian bridge.Later Dudley reformulated Donsker's result to avoid the problem of measurability and the need of the Skorokhod metric. One can prove that there exist Xi, iid uniform in [0,1] and a sequence of sample-continuous Brownian bridges Bn, such that
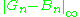
is measurable and converges in probability to 0. An improved version of this result, providing more detail on the rate of convergence, is the Komlós–Major–Tusnády approximation
Komlós–Major–Tusnády approximation
In theory of probability, the Komlós–Major–Tusnády approximation is an approximation of the empirical process by a Gaussian process constructed on the same probability space...
.