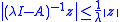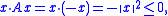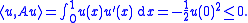Dissipative operator
Encyclopedia
In mathematics
, a dissipative operator is a linear operator A defined on a linear subspace
D(A) of Banach space
X, taking values in X such that for all λ > 0 and all x ∈ D(A)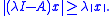
A dissipative operator is called maximally dissipative if it is dissipative and for all λ > 0 the operator λI − A is surjective.
The main importance of dissipative operators is their appearance in the Lumer–Phillips theorem which characterizes maximally dissipative operators as the generators of contraction semigroups.
X of X, by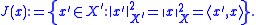
By the Hahn–Banach theorem
this set is nonempty. If X is reflexive, then J(x) consists of a single element. In the Hilbert space
case (using the canonical duality between a Hilbert space and its dual) it consists of the single element x.
Using this notation, A is dissipative if and only if for all x ∈ D(A) there exists a x' ∈ J(x) such that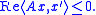
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a dissipative operator is a linear operator A defined on a linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
D(A) of Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
X, taking values in X such that for all λ > 0 and all x ∈ D(A)
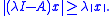
A dissipative operator is called maximally dissipative if it is dissipative and for all λ > 0 the operator λI − A is surjective.
The main importance of dissipative operators is their appearance in the Lumer–Phillips theorem which characterizes maximally dissipative operators as the generators of contraction semigroups.
Properties
A dissipative operator has the following properties- λI − A is injective for all λ > 0 and
-
-
- for all z in the range of λI − A.
- λI − A is surjective for some λ > 0 if and only if it is surjective for all λ > 0. In that case one has (0, ∞) ⊂ ρ(A) (the resolvent setResolvent setIn linear algebra and operator theory, the resolvent set of a linear operator is a set of complex numbers for which the operator is in some sense "well-behaved". The resolvent set plays an important role in the resolvent formalism.-Definitions:...
of A). - A is a closed operatorClosed operatorIn mathematics, specifically in functional analysis, closed linear operators are an important class of linear operators on Banach spaces. They are more general than bounded operators, and therefore not necessarily continuous, but they still retain nice enough properties that one can define the...
if and only if the range of λI − A is closed for some (equivalently: for all) λ > 0.
- λI − A is surjective for some λ > 0 if and only if it is surjective for all λ > 0. In that case one has (0, ∞) ⊂ ρ(A) (the resolvent set
-
Equivalent characterization
Define the duality set of x ∈ X, a subset of the dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
X of X, by
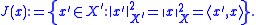
By the Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
this set is nonempty. If X is reflexive, then J(x) consists of a single element. In the Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
case (using the canonical duality between a Hilbert space and its dual) it consists of the single element x.
Using this notation, A is dissipative if and only if for all x ∈ D(A) there exists a x
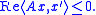
Examples
- For a simple finite-dimensional example, consider n-dimensional Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn with its usual dot productDot productIn mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
. If A denotes the negative of the identity operator, defined on all of Rn, then
- so A is a dissipative operator.
- Consider H = L2([0, 1]; R) with its usual inner product, and let Au = u′ with domain D(A) equal to those functions u in the Sobolev spaceSobolev spaceIn mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
H1([0, 1]; R) with u(1) = 0. D(A) is dense in L2([0, 1]; R). Moreover, for every u in D(A), using integration by partsIntegration by partsIn calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
,
- Hence, A is a dissipative operator.
- Consider H = H02(Ω; R) for an openOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
and connectedConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
domain Ω ⊆ Rn and let A = Δ, the Laplace operatorLaplace operatorIn mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
, defined on the dense subspace of compactly supported smooth functions on Ω. Then, using integration by parts,
- so the Laplacian is a dissipative operator.