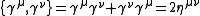Dirac algebra
Encyclopedia
In mathematical physics
, the Dirac algebra is the Clifford algebra
Cℓ1,3(C) which is generated by matrix multiplication
and real and complex linear combination
over the Dirac gamma matrices, introduced by the mathematical physicist P. A. M. Dirac in 1928 in developing the Dirac equation
for spin-½
particles.
These matrices have the defining relation
where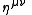
is the Minkowski metric with signature (+ − − −), allowing the definition of a scalar product
where a = Σ aμγμ and b = Σ bνγν.
of the real algebra Cℓ1,3(R), called the space time algebra:
Cℓ1,3(R) differs from Cℓ1,3(C): in Cℓ1,3(R) only real linear combinations of the gamma matrices and their products are allowed.
Proponents of geometric algebra
strive to work with real algebras wherever that is possible. They argue that it is generally possible (and usually enlightening) to identify the presence of an imaginary unit in a physical equation. Such units arise from one of the many quantities in a real Clifford algebra that square to -1, and these have geometric significance because of the properties of the algebra and the interaction of its various subspaces. Some of these proponents also question whether it is necessary or even useful to introduce an additional imaginary unit in the context of the Dirac equation.
However, in contemporary practice, the Dirac algebra rather than the space time algebra continues to be the standard environment the spinor
s of the Dirac equation "live" in.
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, the Dirac algebra is the Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
Cℓ1,3(C) which is generated by matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
and real and complex linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
over the Dirac gamma matrices, introduced by the mathematical physicist P. A. M. Dirac in 1928 in developing the Dirac equation
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
for spin-½
Spin-½
In quantum mechanics, spin is an intrinsic property of all elementary particles. Fermions, the particles that constitute ordinary matter, have half-integer spin. Spin-½ particles constitute an important subset of such fermions. All known elementary fermions have a spin of ½.- Overview :Particles...
particles.
These matrices have the defining relation
where
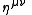is the Minkowski metric with signature (+ − − −), allowing the definition of a scalar product
where a = Σ aμγμ and b = Σ bνγν.
Cℓ1,3(C) and Cℓ1,3(R)
The Dirac algebra can be regarded as a complexificationComplexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
of the real algebra Cℓ1,3(R), called the space time algebra:
Cℓ1,3(R) differs from Cℓ1,3(C): in Cℓ1,3(R) only real linear combinations of the gamma matrices and their products are allowed.
Proponents of geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
strive to work with real algebras wherever that is possible. They argue that it is generally possible (and usually enlightening) to identify the presence of an imaginary unit in a physical equation. Such units arise from one of the many quantities in a real Clifford algebra that square to -1, and these have geometric significance because of the properties of the algebra and the interaction of its various subspaces. Some of these proponents also question whether it is necessary or even useful to introduce an additional imaginary unit in the context of the Dirac equation.
However, in contemporary practice, the Dirac algebra rather than the space time algebra continues to be the standard environment the spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s of the Dirac equation "live" in.