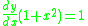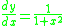Differentiation of trigonometric functions
Encyclopedia
| Function | Derivative |
|---|---|
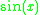 |
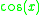 |
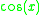 |
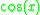 |
 |
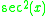 |
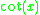 |
 |
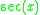 |
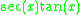 |
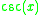 |
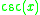 |
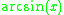 |
 |
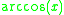 |
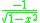 |
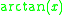 |
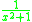 |
The differentiation of trigonometric functions is the mathematical process of finding the rate at which a trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
changes with respect to a variable--the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the trigonometric function. Commonplace trigonometric functions include sin(x), cos(x) and tan(x). For example, in differentiating f(x) = sin(x), one is calculating a function f ′(x) which computes the rate of change of sin(x) at a particular point a. The value of the rate of change at a is thus given by f ′(a). Knowledge of differentiation from first principles is required, along with competence in the use of trigonometric identities and limits. All functions involve the arbitrary variable x, with all differentiation performed with respect to x.
It turns out that once one knows the deriatives of sin(x) and cos(x), one can easily compute the derivatives of the other circular trigonometric functions because they can all be expressed in terms of sine or cosine; the quotient rule is then implemented to differentiate this expression. Proofs of the derivatives of sin(x) and cos(x) are given in the proofs section; the results are quoted in order to give proofs of the derivatives of the other circular trigonometric functions. Finding the derivatives of the inverse trigonometric functions involves using implicit differentiation and the derivatives of regular trigonometric functions also given in the proofs section.
Derivatives of trigonometric functions and their inverses
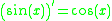
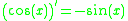
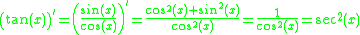
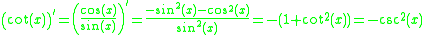
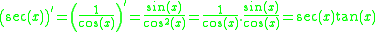
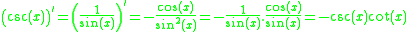
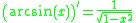
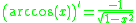
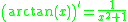
Limit of sin(θ)/θ as θ → 0
Consider the unit circle shown in the figure. Assume that the angle, say θ, made by the chordChord (geometry)
A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
s OB and OC is small, e.g. less than π/2 radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s, Let T1 denote the triangle with vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
O, B and C. Let S denote the sector
Circular sector
A circular sector or circle sector, is the portion of a disk enclosed by two radii and an arc, where the smaller area is known as the minor sector and the larger being the major sector. In the diagram, θ is the central angle in radians, r the radius of the circle, and L is the arc length of the...
given by the chords OB and OC (i.e. the "slice of pizza" given by cutting along the lines OB and OC). Let T2 denote the triangle with vertices O, B and D. Clearly, the area of T1 is less than the area of S, which is itself less than the area of T2, i.e.
The area of a triangle is given by one half of the length of the base multiplied by the height. Using u to denote the chosen unit of measurement, we find that the area of T1 is exactly × ||OB|| × ||CA|| = × 1 × sin(θ) = ·sin(θ) u2. The area of the sector S is exactly ·θ u2. Finally, the area of the triangle T2 is exactly × ||OB|| × ||BD|| = ·tan(θ) u2.
Since we find that, for small θ,
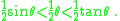
(Recall that .) If this is true then multiplication by two gives . Take the reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
s of each term will reverse the inequalities, e.g. while It follows that
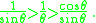
Since θ is small, and so less than π/2 radians, , it follows that We can multiply through by the positive quantity sin(θ) without changing the inequalities; whence:

This tells us that for very small θ, sin(θ)/θ is less than 1, but is bigger than cos(θ). However, as θ becomes smaller, cos(θ) becomes bigger and gets closer to 1 (see the cosine graph). The inequality tells us that sin(θ)/θ is always less than 1 and more than cos(θ); but as θ becomes smaller, cos(θ) gets closer to 1. So, sin(θ)/θ is sandwiched, or squeezed, between 1 and cos(θ) as θ becomes smaller and smaller. Obviously, the number 1 is fixed, and so as θ becomes smaller and smaller, cos(θ) forces sin(θ)/θ to move closer and closer to 1. This is made precise by the so-called sandwich theorem, also known as the squeeze theorem.
Limit of [cos(θ) – 1]/θ as θ → 0
The last section enables us to calculate this new limit easily. We find that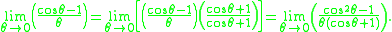
The well-known identity tells us that
Using this, the fact that the limit of a product is the product of the limit, and the result from the last section, we find that

Derivative of the sine function
To calculate the derivative of the sine function, sin(θ) we use first principals. By definition:
Using the well-known angle formula and the two limits from this section and this section, we find that

Derivative of the cosine function
To calculate the derivative of the cosine function, cos(θ) we use first principals. By definition: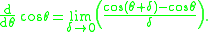
Using the well-known angle formula and the two limits from this section and this section, we find that

Proofs of derivatives of inverse trigonometric functions
The following derivatives are found by setting a variableVariable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
y equal to the inverse trigonometric function
Inverse trigonometric function
In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions with suitably restricted domains .The notations sin−1, cos−1, etc...
that we wish to take the derivative of. Using implicit differentiation and then solving for dy/dx, the derivative of the inverse function is found in terms of y. To convert dy/dx back into being in terms of x, we can draw a reference triangle on the unit circle, letting θ be y. Using the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
and the definition of the regular trigonometric functions, we can finally express dy/dx in terms of x.
Differentiating the inverse sine function
We let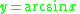
Where
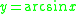
Then
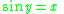
Using implicit differentiation and solving for dy/dx:
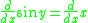
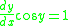
Substituting
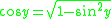 in from above,
in from above,
Substituting
 in from above,
in from above,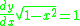

Differentiating the inverse cosine function
We let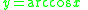
Where

Then
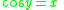
Using implicit differentiation and solving for dy/dx:
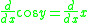
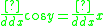
Substituting
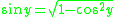 in from above, we get
in from above, we get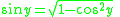
Substituting
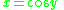 in from above, we get
in from above, we get
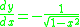
Differentiating the inverse tangent function
We let
Where

Then
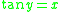
Using implicit differentiation and solving for dy/dx:
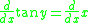
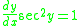
Substituting
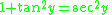 into the above,
into the above,
Substituting
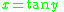 in from above,
in from above,