
Dice's coefficient
Encyclopedia
Dice's coefficient, named after Lee Raymond Dice and also known as the Dice coefficient, is a similarity measure over sets:

It is identical to the Sørensen similarity index
, and is occasionally referred to as the Sørensen-Dice coefficient.
It is not very different in form from the Jaccard index
but has some different properties.
The function ranges between zero and one, like Jaccard. Unlike Jaccard, the corresponding difference function
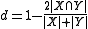
is not a proper distance metric as it does not possess the property of triangle inequality. The simplest counterexample of this is given by the three sets {a), {b}, and {a,b}, the distance between the first two
being 1, and the difference between the third and each of the others being one-third.
Similarly to Jaccard, the set operations can be expressed in terms of vector operations over binary vectors A and B:
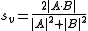
which gives the same outcome over binary vectors and also gives a more general similarity metric over vectors in general terms.
For sets X and Y of keywords used in information retrieval
, the coefficient may be defined as twice the shared information (intersection) over the sum of cardinalities :
When taken as a string similarity measure, the coefficient may be calculated for two strings, x and y using bigram
s as follows:
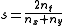
where nt is the number of character bigrams found in both strings, nx is the number of bigrams in string x and ny is the number of bigrams in string y. For example, to calculate the similarity between:
We would find the set of bigrams in each word:
Each set has four elements, and the intersection of these two sets has only one element:
Inserting these numbers into the formula, we calculate, s = (2 · 1) / (4 + 4) = 0.25.

It is identical to the Sørensen similarity index
Sørensen similarity index
The Sørensen index, also known as Sørensen’s similarity coefficient, is a statistic used for comparing the similarity of two samples. It was developed by the botanist Thorvald Sørensen and published in 1948....
, and is occasionally referred to as the Sørensen-Dice coefficient.
It is not very different in form from the Jaccard index
Jaccard index
The Jaccard index, also known as the Jaccard similarity coefficient , is a statistic used for comparing the similarity and diversity of sample sets....
but has some different properties.
The function ranges between zero and one, like Jaccard. Unlike Jaccard, the corresponding difference function
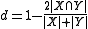
is not a proper distance metric as it does not possess the property of triangle inequality. The simplest counterexample of this is given by the three sets {a), {b}, and {a,b}, the distance between the first two
being 1, and the difference between the third and each of the others being one-third.
Similarly to Jaccard, the set operations can be expressed in terms of vector operations over binary vectors A and B:
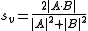
which gives the same outcome over binary vectors and also gives a more general similarity metric over vectors in general terms.
For sets X and Y of keywords used in information retrieval
Information retrieval
Information retrieval is the area of study concerned with searching for documents, for information within documents, and for metadata about documents, as well as that of searching structured storage, relational databases, and the World Wide Web...
, the coefficient may be defined as twice the shared information (intersection) over the sum of cardinalities :
When taken as a string similarity measure, the coefficient may be calculated for two strings, x and y using bigram
Bigram
Bigrams or digrams are groups of two written letters, two syllables, or two words, and are very commonly used as the basis for simple statistical analysis of text. They are used in one of the most successful language models for speech recognition...
s as follows:
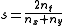
where nt is the number of character bigrams found in both strings, nx is the number of bigrams in string x and ny is the number of bigrams in string y. For example, to calculate the similarity between:
nightnacht
We would find the set of bigrams in each word:
- {
ni,ig,gh,ht} - {
na,ac,ch,ht}
Each set has four elements, and the intersection of these two sets has only one element:
ht.Inserting these numbers into the formula, we calculate, s = (2 · 1) / (4 + 4) = 0.25.
See also
- Jaccard indexJaccard indexThe Jaccard index, also known as the Jaccard similarity coefficient , is a statistic used for comparing the similarity and diversity of sample sets....
, which is equivalent: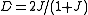 and
and 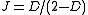
- Tversky indexTversky indexThe Tversky index, named after Amos Tversky, is an asymmetric similarity measure that compares a variant to a prototype. The Tversky index can be seen as a generalization of Dice's coefficient and Tanimoto coefficient....
- Levenshtein distanceLevenshtein distanceIn information theory and computer science, the Levenshtein distance is a string metric for measuring the amount of difference between two sequences...
- Sørensen similarity indexSørensen similarity indexThe Sørensen index, also known as Sørensen’s similarity coefficient, is a statistic used for comparing the similarity of two samples. It was developed by the botanist Thorvald Sørensen and published in 1948....

