
Tversky index
Encyclopedia
The Tversky index, named after Amos Tversky
, is an asymmetric similarity measure that compares a variant to a prototype. The Tversky index can be seen as a generalization of Dice's coefficient and Tanimoto coefficient.
For sets X and Y of keywords used in information retrieval
, the Tversky index is a number between 0 and 1 given by
 ,
,
where are parameters of the Tversky index. Setting
are parameters of the Tversky index. Setting  produces the Tanimono coefficient; setting
produces the Tanimono coefficient; setting 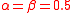 produces Dice's coefficient.
produces Dice's coefficient.
If we consider X to be the prototype and Y to be the variant, then corresponds to the weight of the prototype and
corresponds to the weight of the prototype and  corresponds to the weight of the variant. Tversky measures with
corresponds to the weight of the variant. Tversky measures with  are of special interest.
are of special interest.
Because of the inherent asymmetry, the Tversky index does not meet the criteria for a similarity metric.
Amos Tversky
Amos Nathan Tversky, was a cognitive and mathematical psychologist, a pioneer of cognitive science, a longtime collaborator of Daniel Kahneman, and a key figure in the discovery of systematic human cognitive bias and handling of risk. Much of his early work concerned the foundations of measurement...
, is an asymmetric similarity measure that compares a variant to a prototype. The Tversky index can be seen as a generalization of Dice's coefficient and Tanimoto coefficient.
For sets X and Y of keywords used in information retrieval
Information retrieval
Information retrieval is the area of study concerned with searching for documents, for information within documents, and for metadata about documents, as well as that of searching structured storage, relational databases, and the World Wide Web...
, the Tversky index is a number between 0 and 1 given by
 ,
,where
 are parameters of the Tversky index. Setting
are parameters of the Tversky index. Setting  produces the Tanimono coefficient; setting
produces the Tanimono coefficient; setting 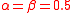 produces Dice's coefficient.
produces Dice's coefficient.If we consider X to be the prototype and Y to be the variant, then
 corresponds to the weight of the prototype and
corresponds to the weight of the prototype and  corresponds to the weight of the variant. Tversky measures with
corresponds to the weight of the variant. Tversky measures with  are of special interest.
are of special interest.Because of the inherent asymmetry, the Tversky index does not meet the criteria for a similarity metric.

