Development (topology)
Encyclopedia
In the mathematical field of topology
, a development is a countable collection of open covers of a topological space
that satisfies certain separation axiom
s.
Let
be a topological space. A development for 
is a countable collection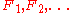 
of open coverings of 
, such that for any closed subset 
and any point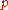 
in the complement
of
, there exists a cover 
such that no element of 
which contains 
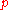intersects 
. A space with a development is called developable.
A development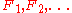
such that 
for all 
is called a nested development. A theorem from Vickery states that every developable space in fact has a nested development. If 
is a refinement of 
, for all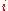 
, then the development is called a refined development.
Vickery's theorem implies that a topological space is a Moore space
if and only if it is regular
and developable.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a development is a countable collection of open covers of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
that satisfies certain separation axiom
Separation axiom
In topology and related fields of mathematics, there are several restrictions that one often makes on the kinds of topological spaces that one wishes to consider. Some of these restrictions are given by the separation axioms...
s.
Let
be a topological space. A development for is a countable collection 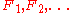of open coverings of , such that for any closed subset and any point 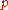in the complementComplement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of
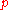, there exists a cover such that no element of which contains intersects . A space with a development is called developable.A development
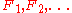such that for all is called a nested development. A theorem from Vickery states that every developable space in fact has a nested development. If is a refinement of , for all , then the development is called a refined development.Vickery's theorem implies that a topological space is a Moore space
Moore space (topology)
In mathematics, more specifically point-set topology, a Moore space is a developable regular Hausdorff space. Equivalently, a topological space X is a Moore space if the following conditions hold:...
if and only if it is regular
Regular space
In topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
and developable.