
Delta method
Encyclopedia
In statistics
, the delta method is a method for deriving an approximate probability distribution
for a function
of an asymptotically normal statistical estimator
from knowledge of the limiting variance
of that estimator. More broadly, the delta method may be considered a fairly general central limit theorem
.

where θ and σ2 are finite valued constants and denotes convergence in distribution, it is the case that
denotes convergence in distribution, it is the case that
for any function g satisfying the property that exists and is non-zero valued. (The final restriction is really only needed for purposes of clarity in argument and application. Should the first derivative evaluate to zero at θ, then the delta method may be extended via use of a second or higher order Taylor series
expansion.)
. To begin, we use the Mean value theorem
:
where lies between Xn and θ.
lies between Xn and θ.
Note that since implies
implies  and since is continuous, applying the continuous mapping theorem
and since is continuous, applying the continuous mapping theorem
yields
where denotes convergence in probability.
denotes convergence in probability.
Rearranging the terms and multiplying by gives
gives
Since
by assumption, it follows immediately from appeal to Slutsky's Theorem that
This concludes the proof.
estimator
B converges in probability to its true value β, and often a central limit theorem
can be applied to obtain asymptotic normality:

where n is the number of observations and Σ is a (symmetric positive semi-definite) covariance matrix. Suppose we want to estimate the variance of a function h of the estimator B. Keeping only the first two terms of the Taylor series
, and using vector notation for the gradient
, we can estimate h(B) as

which implies the variance of h(B) is approximately
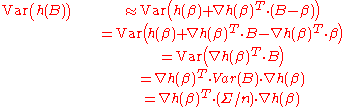
One can use the mean value theorem
(for real-valued functions of many variables) to see that this does not rely on taking first order approximation.
The delta method therefore implies that

or in univariate terms,


we can apply the Delta method with to see
Hence, the variance of is approximately
is approximately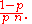
Moreoever, if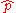 and
and 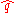 are estimates of different group rates from independent samples of sizes n and m respectively, then the logarithm of the estimated relative risk
are estimates of different group rates from independent samples of sizes n and m respectively, then the logarithm of the estimated relative risk
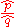 is approximately normally distributed with variance that can be estimated by
is approximately normally distributed with variance that can be estimated by 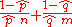 . This is useful to construct a hypothesis test or to make a confidence interval for the relative risk.
. This is useful to construct a hypothesis test or to make a confidence interval for the relative risk.
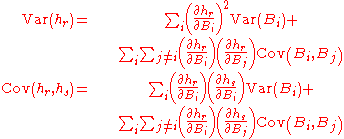
where hr is the rth element of h(B) and Biis the ith element of B. The only difference is that Klein stated these as identities, whereas they are actually approximations.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the delta method is a method for deriving an approximate probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
for a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of an asymptotically normal statistical estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
from knowledge of the limiting variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of that estimator. More broadly, the delta method may be considered a fairly general central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
.
Univariate delta method
While the delta method generalizes easily to a multivariate setting, careful motivation of the technique is more easily demonstrated in univariate terms. Roughly, for some sequence of random variables Xn satisfying
where θ and σ2 are finite valued constants and
 denotes convergence in distribution, it is the case that
denotes convergence in distribution, it is the case that
for any function g satisfying the property that exists and is non-zero valued. (The final restriction is really only needed for purposes of clarity in argument and application. Should the first derivative evaluate to zero at θ, then the delta method may be extended via use of a second or higher order Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion.)
Proof in the univariate case
Demonstration of this result is fairly straightforward under the assumption that is continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. To begin, we use the Mean value theorem
Mean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
:

where
 lies between Xn and θ.
lies between Xn and θ.Note that since
 implies
implies  and since is continuous, applying the continuous mapping theorem
and since is continuous, applying the continuous mapping theoremContinuous mapping theorem
In probability theory, the continuous mapping theorem states that continuous functions are limit-preserving even if their arguments are sequences of random variables. A continuous function, in Heine’s definition, is such a function that maps convergent sequences into convergent sequences: if xn → x...
yields

where
 denotes convergence in probability.
denotes convergence in probability.Rearranging the terms and multiplying by
 gives
gives
Since

by assumption, it follows immediately from appeal to Slutsky's Theorem that

This concludes the proof.
Motivation of multivariate delta method
By definition, a consistentConsistency (statistics)
In statistics, consistency of procedures such as confidence intervals or hypothesis tests involves their behaviour as the number of items in the data-set to which they are applied increases indefinitely...
estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
B converges in probability to its true value β, and often a central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
can be applied to obtain asymptotic normality:

where n is the number of observations and Σ is a (symmetric positive semi-definite) covariance matrix. Suppose we want to estimate the variance of a function h of the estimator B. Keeping only the first two terms of the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
, and using vector notation for the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
, we can estimate h(B) as

which implies the variance of h(B) is approximately
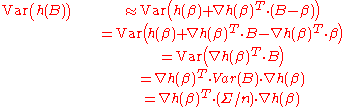
One can use the mean value theorem
Mean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
(for real-valued functions of many variables) to see that this does not rely on taking first order approximation.
The delta method therefore implies that

or in univariate terms,

Example
Suppose Xn is Binomial with parameters p and n. Since
we can apply the Delta method with to see

Hence, the variance of
 is approximately
is approximately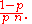
Moreoever, if
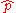 and
and 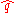 are estimates of different group rates from independent samples of sizes n and m respectively, then the logarithm of the estimated relative risk
are estimates of different group rates from independent samples of sizes n and m respectively, then the logarithm of the estimated relative riskRelative risk
In statistics and mathematical epidemiology, relative risk is the risk of an event relative to exposure. Relative risk is a ratio of the probability of the event occurring in the exposed group versus a non-exposed group....
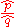 is approximately normally distributed with variance that can be estimated by
is approximately normally distributed with variance that can be estimated by 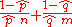 . This is useful to construct a hypothesis test or to make a confidence interval for the relative risk.
. This is useful to construct a hypothesis test or to make a confidence interval for the relative risk.Note
The delta method is often used in a form that is essentially identical to that above, but without the assumption that Xn or B is asymptotically normal. Often the only context is that the variance is "small". The results then just give approximations to the means and covariances of the transformed quantities. For example, the formulae presented in Klein (1953, p. 258) are: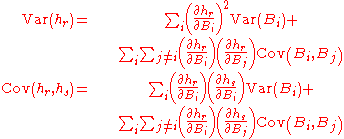
where hr is the rth element of h(B) and Biis the ith element of B. The only difference is that Klein stated these as identities, whereas they are actually approximations.

