
Quadratic growth
Encyclopedia
In mathematics
, a function or sequence is said to exhibit quadratic growth when its values are proportional
to the square of the function argument or sequence position, in the limit as the argument or sequence position goes to infinity. That is, in big Theta notation
,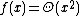 .
.
Examples of quadratic growth include
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a function or sequence is said to exhibit quadratic growth when its values are proportional
Proportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
to the square of the function argument or sequence position, in the limit as the argument or sequence position goes to infinity. That is, in big Theta notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
,
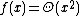 .
.Examples of quadratic growth include
- Any quadratic polynomialQuadratic polynomialIn mathematics, a quadratic polynomial or quadratic is a polynomial of degree two, also called second-order polynomial. That means the exponents of the polynomial's variables are no larger than 2...
.
- Certain integer sequenceInteger sequenceIn mathematics, an integer sequence is a sequence of integers.An integer sequence may be specified explicitly by giving a formula for its nth term, or implicitly by giving a relationship between its terms...
s such as the triangular numberTriangular numberA triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
s. The nth triangular number has value n(n+1)/2, approximately n2/2.
- The amount of time taken in the worst case by certain algorithmAlgorithmIn mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s, such as insertion sortInsertion sortInsertion sort is a simple sorting algorithm: a comparison sort in which the sorted array is built one entry at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort...
, as a function of the input length.
- The numbers of live cells in space-filling cellular automatonCellular automatonA cellular automaton is a discrete model studied in computability theory, mathematics, physics, complexity science, theoretical biology and microstructure modeling. It consists of a regular grid of cells, each in one of a finite number of states, such as "On" and "Off"...
patterns such as the Breeder (CA), as a function of the number of time steps for which the pattern is simulated.
- Metcalfe's lawMetcalfe's lawMetcalfe's law states that the value of a telecommunications network is proportional to the square of the number of connected usersof the system...
stating that the value of a communications network grows quadratically as a function of its number of users

