
De Sitter invariant special relativity
Encyclopedia
In mathematical physics
, de Sitter invariant special relativity is the speculative idea that the fundamental symmetry group
of spacetime
is the Indefinite orthogonal group SO(4,1), that of de Sitter space
. In the standard theory of General Relativity
, de Sitter space is a highly symmetrical special vacuum solution
, which requires a cosmological constant
or the stress-energy of a constant scalar field
to sustain.
The idea of de Sitter invariant relativity is to require that the laws of physics are not fundamentally invariant under the Poincaré group
of special relativity
, but under the symmetry group of de Sitter space instead. With this assumption, empty space automatically has de Sitter symmetry, and what would normally be called the cosmological constant in General Relativity becomes a fundamental dimensional parameter describing the symmetry structure of space-time.
First proposed by Luigi Fantappiè
in 1954, the theory remained obscure until it was rediscovered in 1968 by Henri Bacry
and Jean-Marc Lévy-Leblond
. In 1972, Freeman Dyson
popularized it as a hypothetical road by which mathematicians could have guessed part of the structure of General Relativity
before it was discovered. The discovery of the accelerating expansion of the universe
has led to a revival of interest in deSitter invariant theories, in conjunction with other speculative proposals for new physics, like doubly special relativity.
and Jean-Marc Lévy-Leblond
showed that the de Sitter group was the most general group compatible with isotropy, homogeneity and boost invariance. Later, Freeman Dyson
advocated this as an approach to making the mathematical structure of General Relativity more self-evident.
Minkowski
's unification of space and time within special relativity
replaces the Galilean group of Newtonian mechanics with the Lorentz group
. This is called a unification of space and time because the Lorentz group is simple
, while the Galilean group is a semi-direct product of rotations and Galilean boosts
. This means that the Lorentz group mixes up space and time so that they cannot be disentangled, while the Galilean group treats time as a parameter with different units of measurement than space.
An analogous thing can be made to happen with the ordinary rotation group in three dimensions. If you imagine a nearly-flat world, one in which pancake-like creatures wander around on a pancake flat world, their conventional unit of height might be the micrometre
 , since that's how high typical structures are in their world, while their x and y axis could be the meter, because that's the size of their body. Such creatures would describe the basic symmetry structure of their world as SO(2), rotations in the x-y plane. Later on, they might discover rotations into the z axis— and in their every-day experience such rotations would always be by an infinitesimal angle, so that these z-rotations would commute with each other.
, since that's how high typical structures are in their world, while their x and y axis could be the meter, because that's the size of their body. Such creatures would describe the basic symmetry structure of their world as SO(2), rotations in the x-y plane. Later on, they might discover rotations into the z axis— and in their every-day experience such rotations would always be by an infinitesimal angle, so that these z-rotations would commute with each other.
The rotations into the z-axis would tilt objects by an infinitesimal amount. The tilt in the x-z plane would be one parameter, and the tilt in the y-z plane another. The symmetry group of this pancake world is SO(2) semidirect product with R2, meaning that a two-dimensional rotation plus two extra parameters, the x-tilt and the y-tilt. The reason it is a semidirect product is that, when you rotate, the x-tilt and the y-tilt rotate into each other, since they form a vector
and not two scalar
s. In this world, the difference in height between two objects at the same x, y would be a rotationally invariant quantity unrelated to length and width. The z coordinate is completely separate from x and y.
But eventually, experiments at large angles would convince the creatures that the actual symmetry of the world is SO(3). Then they would understand that z is really the same as x and y, since they can be mixed up by rotations. The SO(2) semidirect product R2 limit would be understood as the limit that the free parameter , the ratio of the height-unit
, the ratio of the height-unit  to the length-unit
to the length-unit  , approaches 0. The Lorentz group is analogous— it is a simple group that turns into the Galilean group when the unit of time is made long compared to the unit of space, which is the limit
, approaches 0. The Lorentz group is analogous— it is a simple group that turns into the Galilean group when the unit of time is made long compared to the unit of space, which is the limit  .
.
But the symmetry group of special relativity is not entirely simple because there are still translations. The Lorentz group are the transformations that keep the origin fixed, but translations are not included. The full Poincaré group is the semi-direct product of translations with the Lorentz group. But if you take the unification idea to its logical conclusion then not only are boosts non-commutative but translations
should be non-commutative too.
In the pancake world, this would happen if the creatures were living on an enormous sphere, not a plane. In this case, when they wander around their sphere, they would eventually come to realize that translations are not entirely separate from rotations, because if they move around on the surface of a sphere, when they come back to where they started, they find that they have been rotated by the holonomy
of parallel transport
on the sphere. If the universe is the same everywhere (homogenous) and there are no preferred directions (isotropic), then there are not many options for the symmetry group: they either live on a flat plane, or on a sphere with everywhere constant positive curvature, or on a Lobachevski plane with constant negative curvature. If they are not living on the plane, they can describe positions using dimensionless angles, the same parameters that describe rotations, so that translations and rotations are nominally unified.
In relativity, if translations mix up nontrivially with rotations, but the universe is still homogeneous
and isotropic, the only options are that space-time has a uniform scalar curvature. If the curvature is positive, the analog of the sphere case for the two-dimensional creatures, the space-time is de Sitter and the symmetry group of spacetime is a de Sitter group rather than the Poincaré group
.
De Sitter special relativity postulates that the empty space has de Sitter symmetry as a fundamental law of nature. This means that spacetime is slightly curved even in the absence of matter or energy. This residual curvature is caused by a positive cosmological constant
 to be determined by observation. Due to the small magnitude of the constant, then special relativity with the Poincaré group is more than accurate enough for all practical purposes.
to be determined by observation. Due to the small magnitude of the constant, then special relativity with the Poincaré group is more than accurate enough for all practical purposes.
Modern proponents of this idea, such as S. Cacciatori, V. Gorini and A. Kamenshchik, have reinterpreted this theory as physics, not just mathematics. They believe that the acceleration of the expansion of the universe is not all due to vacuum energy
, but at least partly due to the kinematics of the de Sitter group
, which in their view is the correct symmetry group of space time, replacing the Lorentz group
.
A modification of this idea allows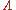 to change with time, so that inflation
to change with time, so that inflation
may come from the cosmological constant being larger near the big bang
than nowadays. It can also be viewed as a different approach to the problem of quantum gravity
.
generalizes the Galilean group for high–velocity kinematics
, meaning that when all velocities are small the Lorentz group 'becomes' the Galilean group. (This can be made precise with İnönü
and Wigner's concept of group contraction.) Similarly, the de Sitter group generalizes Poincaré for long distance kinematics, meaning that when magnitudes of all translations are small compared to the de Sitter radius, the de Sitter group becomes the Lorentz group. In quantum mechanics, short distances are probed by high energies, so that for energies larger than a very small cosmological scale, the Poincaré group is a good approximation to the de Sitter group.
In de Sitter relativity, the cosmological constant is no longer a free parameter of the same type, it is determined by the de Sitter radius, a fundamental quantity that determines the commutation relation of translation with rotations/boosts. This means that the theory of de Sitter relativity might be able to provide insight on the value of the cosmological constant, perhaps explaining the cosmic coincidence. Unfortunately, the de Sitter radius, which is interchangeable with the cosmological constant, is an adjustable parameter in de Sitter relativity, so the theory requires a separate condition to determine its value.
When a cosmological constant is viewed as a kinematic parameter, the definitions of energy and momentum must be changed from those of special relativity. These changes could modify significantly the physics of the early universe, if the cosmological constant was bigger back then. Some speculate that a high energy experiment could modify the local structure of spacetime from Minkowski space
to de Sitter space
with a large cosmological constant for a short period of time, and this might eventually be tested in the existing or planned colliders.
, energy
and momentum
, and is consequently valid at all energy scales. A relationship between doubly special relativity, de Sitter space and general relativity is described by Derek Wise. See also MacDowell-Mansouri action
.
Newton-Hooke: de Sitter special relativity in the limit as v<
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, de Sitter invariant special relativity is the speculative idea that the fundamental symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
is the Indefinite orthogonal group SO(4,1), that of de Sitter space
De Sitter space
In mathematics and physics, a de Sitter space is the analog in Minkowski space, or spacetime, of a sphere in ordinary, Euclidean space. The n-dimensional de Sitter space , denoted dS_n, is the Lorentzian manifold analog of an n-sphere ; it is maximally symmetric, has constant positive curvature,...
. In the standard theory of General Relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, de Sitter space is a highly symmetrical special vacuum solution
Vacuum solution
A vacuum solution is a solution of a field equation in which the sources of the field are taken to be identically zero. That is, such field equations are written without matter interaction .-Examples:...
, which requires a cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
or the stress-energy of a constant scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
to sustain.
The idea of de Sitter invariant relativity is to require that the laws of physics are not fundamentally invariant under the Poincaré group
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, but under the symmetry group of de Sitter space instead. With this assumption, empty space automatically has de Sitter symmetry, and what would normally be called the cosmological constant in General Relativity becomes a fundamental dimensional parameter describing the symmetry structure of space-time.
First proposed by Luigi Fantappiè
Luigi Fantappiè
Luigi Fantappiè was an Italian mathematician, known for work in mathematical analysis and for creating the theory of analytic functionals: he was a student and follower of Vito Volterra. Later in life he proposed scientific theories of sweeping scope.He was born in Viterbo, and studied at the...
in 1954, the theory remained obscure until it was rediscovered in 1968 by Henri Bacry
Henri Bacry
Henri Bacry is Professor Emeritus at the Université de la Méditerranée. Henri Bacry was assistant of physics at the Faculté des Sciences d'Alger and then Professor of mathematics at Lycée Bugeaud, before becoming, in 1969, Professor at the Faculté des Sciences de Marseille. He was a member of the...
and Jean-Marc Lévy-Leblond
Jean-Marc Lévy-Leblond
Jean-Marc Lévy-Leblond, born in 1940, is a physicist and essayist.After a doctorate in Theoretical Physics at the université d’Orsay in 1965, he was successively in charge of research at CNRS, lecturer at the université de Nice, a professor at the Paris Diderot University, and at Nice, where he...
. In 1972, Freeman Dyson
Freeman Dyson
Freeman John Dyson FRS is a British-born American theoretical physicist and mathematician, famous for his work in quantum field theory, solid-state physics, astronomy and nuclear engineering. Dyson is a member of the Board of Sponsors of the Bulletin of the Atomic Scientists...
popularized it as a hypothetical road by which mathematicians could have guessed part of the structure of General Relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
before it was discovered. The discovery of the accelerating expansion of the universe
Accelerating universe
The accelerating universe is the observation that the universe appears to be expanding at an increasing rate, which in formal terms means that the cosmic scale factor a has a positive second derivative, implying that the velocity at which a given galaxy is receding from us should be continually...
has led to a revival of interest in deSitter invariant theories, in conjunction with other speculative proposals for new physics, like doubly special relativity.
Introduction
De Sitter himself suggested that space-time curvature might not be due solely to gravity but he did not give any mathematical details of how this could be accomplished. In 1968 Henri BacryHenri Bacry
Henri Bacry is Professor Emeritus at the Université de la Méditerranée. Henri Bacry was assistant of physics at the Faculté des Sciences d'Alger and then Professor of mathematics at Lycée Bugeaud, before becoming, in 1969, Professor at the Faculté des Sciences de Marseille. He was a member of the...
and Jean-Marc Lévy-Leblond
Jean-Marc Lévy-Leblond
Jean-Marc Lévy-Leblond, born in 1940, is a physicist and essayist.After a doctorate in Theoretical Physics at the université d’Orsay in 1965, he was successively in charge of research at CNRS, lecturer at the université de Nice, a professor at the Paris Diderot University, and at Nice, where he...
showed that the de Sitter group was the most general group compatible with isotropy, homogeneity and boost invariance. Later, Freeman Dyson
Freeman Dyson
Freeman John Dyson FRS is a British-born American theoretical physicist and mathematician, famous for his work in quantum field theory, solid-state physics, astronomy and nuclear engineering. Dyson is a member of the Board of Sponsors of the Bulletin of the Atomic Scientists...
advocated this as an approach to making the mathematical structure of General Relativity more self-evident.
Minkowski
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
's unification of space and time within special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
replaces the Galilean group of Newtonian mechanics with the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
. This is called a unification of space and time because the Lorentz group is simple
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
, while the Galilean group is a semi-direct product of rotations and Galilean boosts
Galilean transformation
The Galilean transformation is used to transform between the coordinates of two reference frames which differ only by constant relative motion within the constructs of Newtonian physics. This is the passive transformation point of view...
. This means that the Lorentz group mixes up space and time so that they cannot be disentangled, while the Galilean group treats time as a parameter with different units of measurement than space.
An analogous thing can be made to happen with the ordinary rotation group in three dimensions. If you imagine a nearly-flat world, one in which pancake-like creatures wander around on a pancake flat world, their conventional unit of height might be the micrometre
Micrometre
A micrometer , is by definition 1×10-6 of a meter .In plain English, it means one-millionth of a meter . Its unit symbol in the International System of Units is μm...
 , since that's how high typical structures are in their world, while their x and y axis could be the meter, because that's the size of their body. Such creatures would describe the basic symmetry structure of their world as SO(2), rotations in the x-y plane. Later on, they might discover rotations into the z axis— and in their every-day experience such rotations would always be by an infinitesimal angle, so that these z-rotations would commute with each other.
, since that's how high typical structures are in their world, while their x and y axis could be the meter, because that's the size of their body. Such creatures would describe the basic symmetry structure of their world as SO(2), rotations in the x-y plane. Later on, they might discover rotations into the z axis— and in their every-day experience such rotations would always be by an infinitesimal angle, so that these z-rotations would commute with each other.The rotations into the z-axis would tilt objects by an infinitesimal amount. The tilt in the x-z plane would be one parameter, and the tilt in the y-z plane another. The symmetry group of this pancake world is SO(2) semidirect product with R2, meaning that a two-dimensional rotation plus two extra parameters, the x-tilt and the y-tilt. The reason it is a semidirect product is that, when you rotate, the x-tilt and the y-tilt rotate into each other, since they form a vector
Visualization software
Visualization software is a range of computer graphics products used to create graphical displays and interfaces for software applications. These products include libraries of graphical components or graphic objects and software editors for building and deploying data displays for applications...
and not two scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
s. In this world, the difference in height between two objects at the same x, y would be a rotationally invariant quantity unrelated to length and width. The z coordinate is completely separate from x and y.
But eventually, experiments at large angles would convince the creatures that the actual symmetry of the world is SO(3). Then they would understand that z is really the same as x and y, since they can be mixed up by rotations. The SO(2) semidirect product R2 limit would be understood as the limit that the free parameter
 , the ratio of the height-unit
, the ratio of the height-unit  to the length-unit
to the length-unit  , approaches 0. The Lorentz group is analogous— it is a simple group that turns into the Galilean group when the unit of time is made long compared to the unit of space, which is the limit
, approaches 0. The Lorentz group is analogous— it is a simple group that turns into the Galilean group when the unit of time is made long compared to the unit of space, which is the limit  .
.But the symmetry group of special relativity is not entirely simple because there are still translations. The Lorentz group are the transformations that keep the origin fixed, but translations are not included. The full Poincaré group is the semi-direct product of translations with the Lorentz group. But if you take the unification idea to its logical conclusion then not only are boosts non-commutative but translations
Translation (physics)
In physics, translation is movement that changes the position of an object, as opposed to rotation. For example, according to Whittaker:...
should be non-commutative too.
In the pancake world, this would happen if the creatures were living on an enormous sphere, not a plane. In this case, when they wander around their sphere, they would eventually come to realize that translations are not entirely separate from rotations, because if they move around on the surface of a sphere, when they come back to where they started, they find that they have been rotated by the holonomy
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
of parallel transport
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
on the sphere. If the universe is the same everywhere (homogenous) and there are no preferred directions (isotropic), then there are not many options for the symmetry group: they either live on a flat plane, or on a sphere with everywhere constant positive curvature, or on a Lobachevski plane with constant negative curvature. If they are not living on the plane, they can describe positions using dimensionless angles, the same parameters that describe rotations, so that translations and rotations are nominally unified.
In relativity, if translations mix up nontrivially with rotations, but the universe is still homogeneous
Homogeneity (physics)
In general, homogeneity is defined as the quality or state of being homogeneous . For instance, a uniform electric field would be compatible with homogeneity...
and isotropic, the only options are that space-time has a uniform scalar curvature. If the curvature is positive, the analog of the sphere case for the two-dimensional creatures, the space-time is de Sitter and the symmetry group of spacetime is a de Sitter group rather than the Poincaré group
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
.
De Sitter special relativity postulates that the empty space has de Sitter symmetry as a fundamental law of nature. This means that spacetime is slightly curved even in the absence of matter or energy. This residual curvature is caused by a positive cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
 to be determined by observation. Due to the small magnitude of the constant, then special relativity with the Poincaré group is more than accurate enough for all practical purposes.
to be determined by observation. Due to the small magnitude of the constant, then special relativity with the Poincaré group is more than accurate enough for all practical purposes.Modern proponents of this idea, such as S. Cacciatori, V. Gorini and A. Kamenshchik, have reinterpreted this theory as physics, not just mathematics. They believe that the acceleration of the expansion of the universe is not all due to vacuum energy
Dark energy
In physical cosmology, astronomy and celestial mechanics, dark energy is a hypothetical form of energy that permeates all of space and tends to accelerate the expansion of the universe. Dark energy is the most accepted theory to explain recent observations that the universe appears to be expanding...
, but at least partly due to the kinematics of the de Sitter group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, which in their view is the correct symmetry group of space time, replacing the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
.
A modification of this idea allows
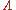 to change with time, so that inflation
to change with time, so that inflationInflation
In economics, inflation is a rise in the general level of prices of goods and services in an economy over a period of time.When the general price level rises, each unit of currency buys fewer goods and services. Consequently, inflation also reflects an erosion in the purchasing power of money – a...
may come from the cosmological constant being larger near the big bang
Big Bang
The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
than nowadays. It can also be viewed as a different approach to the problem of quantum gravity
Quantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
.
High energy
The Poincaré groupPoincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
generalizes the Galilean group for high–velocity kinematics
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
, meaning that when all velocities are small the Lorentz group 'becomes' the Galilean group. (This can be made precise with İnönü
Erdal Inönü
Erdal İnönü was a Turkish physicist and politician. He was the son of Turkey's second president İsmet İnönü...
and Wigner's concept of group contraction.) Similarly, the de Sitter group generalizes Poincaré for long distance kinematics, meaning that when magnitudes of all translations are small compared to the de Sitter radius, the de Sitter group becomes the Lorentz group. In quantum mechanics, short distances are probed by high energies, so that for energies larger than a very small cosmological scale, the Poincaré group is a good approximation to the de Sitter group.
In de Sitter relativity, the cosmological constant is no longer a free parameter of the same type, it is determined by the de Sitter radius, a fundamental quantity that determines the commutation relation of translation with rotations/boosts. This means that the theory of de Sitter relativity might be able to provide insight on the value of the cosmological constant, perhaps explaining the cosmic coincidence. Unfortunately, the de Sitter radius, which is interchangeable with the cosmological constant, is an adjustable parameter in de Sitter relativity, so the theory requires a separate condition to determine its value.
When a cosmological constant is viewed as a kinematic parameter, the definitions of energy and momentum must be changed from those of special relativity. These changes could modify significantly the physics of the early universe, if the cosmological constant was bigger back then. Some speculate that a high energy experiment could modify the local structure of spacetime from Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
to de Sitter space
De Sitter space
In mathematics and physics, a de Sitter space is the analog in Minkowski space, or spacetime, of a sphere in ordinary, Euclidean space. The n-dimensional de Sitter space , denoted dS_n, is the Lorentzian manifold analog of an n-sphere ; it is maximally symmetric, has constant positive curvature,...
with a large cosmological constant for a short period of time, and this might eventually be tested in the existing or planned colliders.
Doubly special relativity
Since the de Sitter group naturally incorporates an invariant length–parameter, de Sitter relativity can be interpreted as an example of the so-called doubly special relativity. There is a fundamental difference, though: whereas in all doubly special relativity models the Lorentz symmetry is violated, in de Sitter relativity it remains as a physical symmetry. A drawback of the usual doubly special relativity models is that they are valid only at the energy scales where ordinary special relativity is supposed to break down, giving rise to a patchwork relativity. On the other hand, de Sitter relativity is found to be invariant under a simultaneous re-scaling of massMass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
, energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
and momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, and is consequently valid at all energy scales. A relationship between doubly special relativity, de Sitter space and general relativity is described by Derek Wise. See also MacDowell-Mansouri action
MacDowell-Mansouri action
The MacDowell–Mansouri action is a mathematical object that is used to derive Einstein's field equations of general relativity....
.
Newton-Hooke: de Sitter special relativity in the limit as v<
In the limit as v≪c, the de Sitter group contracts to the Newton-Hooke group. This implies that in the nonrelativistic limit, objects in de Sitter space have an extra "repulsion" from the origin, objects have a tendency to move away from the center with an outward pointing fictitious forceFictitious forceA fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
proportional to their distance from the origin.
While this setup looks like it picks out a preferred point in space— the center of repulsion— it is more subtly isotropic. If you move to another point, you should transform to the uniformly accelerated frame of reference of an observer at this point, which changes all accelerations to shift the repulsion center to the new origin of coordinates.
What this means is that in a spacetime with non-vanishing curvature, gravity is modified from Newtonian gravity. At distances comparable to the radius of the space, objects feel an additional linear repulsion from the center of coordinates.
History of de Sitter invariant special relativity
- "de Sitter relativity" is the same as the theory of "projective relativity" of Luigi FantappièLuigi FantappièLuigi Fantappiè was an Italian mathematician, known for work in mathematical analysis and for creating the theory of analytic functionals: he was a student and follower of Vito Volterra. Later in life he proposed scientific theories of sweeping scope.He was born in Viterbo, and studied at the...
and Giuseppe ArcidiaconoGiuseppe ArcidiaconoGiuseppe Arcidiacono was an Italian physicist. He was born in Acireale and graduated in physics in Catania in 1951. He began working with Luigi Fantappiè on what they called projective relativity at the Istituto Nazionale di Alta Matematica in Rome. In 1958 he won a scholarship to the Istituto H....
first published in 1954 by Fantappiè and the same as another independent discovery in 1976.
- In 1968 Henri BacryHenri BacryHenri Bacry is Professor Emeritus at the Université de la Méditerranée. Henri Bacry was assistant of physics at the Faculté des Sciences d'Alger and then Professor of mathematics at Lycée Bugeaud, before becoming, in 1969, Professor at the Faculté des Sciences de Marseille. He was a member of the...
and Jean-Marc Lévy-LeblondJean-Marc Lévy-LeblondJean-Marc Lévy-Leblond, born in 1940, is a physicist and essayist.After a doctorate in Theoretical Physics at the université d’Orsay in 1965, he was successively in charge of research at CNRS, lecturer at the université de Nice, a professor at the Paris Diderot University, and at Nice, where he...
published a paper on possible kinematics
- In 1972 Freeman DysonFreeman DysonFreeman John Dyson FRS is a British-born American theoretical physicist and mathematician, famous for his work in quantum field theory, solid-state physics, astronomy and nuclear engineering. Dyson is a member of the Board of Sponsors of the Bulletin of the Atomic Scientists...
further explored this.
- In 1973 Eliano Pessa described how Fantappié-Arcidiacono projective relativity relates to earlier conceptions of projective relativity and to Kaluza Klein theory.
- Han-Ying Guo, Chao-Guang Huang, Zhan Xu, Bin Zhou have used the term "de Sitter special relativity" from 2004 onwards.
- R. Aldrovandi, J.P. Beltrán Almeida and J.G. Pereira have used the terms "de Sitter special relativity" and "de Sitter relativity" starting from their 2007 paper "de Sitter special relativity". This paper was based on previous work on amongst other things: the consequences of a non-vanishing cosmological constant, on doubly special relativity and on the Newton-Hooke group and early work formulating special relativity with a de Sitter space
- From 2006 onwards Ignazio Licata and Leonardo Chiatti have published papers on Fantappié-Arcidiacono theory of relativity pointing out that it is the same thing as de Sitter relativity
- In 2008 S. Cacciatori, V. Gorini and A. Kamenshchik published a paper about the kinematics of de Sitter relativity.
- Papers by other authors include: dSR and the fine structure constant; dSR and dark energy; dSR Hamiltonian Formalism; and De Sitter Thermodynamics from Diamonds’s Temperature, Triply special relativity from six dimensions, Deformed General Relativity and Torsion.
Quantum de Sitter special relativity
There are quantized or quantum versions of de Sitter special relativity.
Early work on formulating a quantum theory in a de Sitter space includes:
Fictitious force
A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
proportional to their distance from the origin.
While this setup looks like it picks out a preferred point in space— the center of repulsion— it is more subtly isotropic. If you move to another point, you should transform to the uniformly accelerated frame of reference of an observer at this point, which changes all accelerations to shift the repulsion center to the new origin of coordinates.
What this means is that in a spacetime with non-vanishing curvature, gravity is modified from Newtonian gravity. At distances comparable to the radius of the space, objects feel an additional linear repulsion from the center of coordinates.
History of de Sitter invariant special relativity
- "de Sitter relativity" is the same as the theory of "projective relativity" of Luigi FantappièLuigi FantappièLuigi Fantappiè was an Italian mathematician, known for work in mathematical analysis and for creating the theory of analytic functionals: he was a student and follower of Vito Volterra. Later in life he proposed scientific theories of sweeping scope.He was born in Viterbo, and studied at the...
and Giuseppe ArcidiaconoGiuseppe ArcidiaconoGiuseppe Arcidiacono was an Italian physicist. He was born in Acireale and graduated in physics in Catania in 1951. He began working with Luigi Fantappiè on what they called projective relativity at the Istituto Nazionale di Alta Matematica in Rome. In 1958 he won a scholarship to the Istituto H....
first published in 1954 by Fantappiè and the same as another independent discovery in 1976. - In 1968 Henri BacryHenri BacryHenri Bacry is Professor Emeritus at the Université de la Méditerranée. Henri Bacry was assistant of physics at the Faculté des Sciences d'Alger and then Professor of mathematics at Lycée Bugeaud, before becoming, in 1969, Professor at the Faculté des Sciences de Marseille. He was a member of the...
and Jean-Marc Lévy-LeblondJean-Marc Lévy-LeblondJean-Marc Lévy-Leblond, born in 1940, is a physicist and essayist.After a doctorate in Theoretical Physics at the université d’Orsay in 1965, he was successively in charge of research at CNRS, lecturer at the université de Nice, a professor at the Paris Diderot University, and at Nice, where he...
published a paper on possible kinematics - In 1972 Freeman DysonFreeman DysonFreeman John Dyson FRS is a British-born American theoretical physicist and mathematician, famous for his work in quantum field theory, solid-state physics, astronomy and nuclear engineering. Dyson is a member of the Board of Sponsors of the Bulletin of the Atomic Scientists...
further explored this. - In 1973 Eliano Pessa described how Fantappié-Arcidiacono projective relativity relates to earlier conceptions of projective relativity and to Kaluza Klein theory.
- Han-Ying Guo, Chao-Guang Huang, Zhan Xu, Bin Zhou have used the term "de Sitter special relativity" from 2004 onwards.
- R. Aldrovandi, J.P. Beltrán Almeida and J.G. Pereira have used the terms "de Sitter special relativity" and "de Sitter relativity" starting from their 2007 paper "de Sitter special relativity". This paper was based on previous work on amongst other things: the consequences of a non-vanishing cosmological constant, on doubly special relativity and on the Newton-Hooke group and early work formulating special relativity with a de Sitter space
- From 2006 onwards Ignazio Licata and Leonardo Chiatti have published papers on Fantappié-Arcidiacono theory of relativity pointing out that it is the same thing as de Sitter relativity
- In 2008 S. Cacciatori, V. Gorini and A. Kamenshchik published a paper about the kinematics of de Sitter relativity.
- Papers by other authors include: dSR and the fine structure constant; dSR and dark energy; dSR Hamiltonian Formalism; and De Sitter Thermodynamics from Diamonds’s Temperature, Triply special relativity from six dimensions, Deformed General Relativity and Torsion.
Quantum de Sitter special relativity
There are quantized or quantum versions of de Sitter special relativity.Early work on formulating a quantum theory in a de Sitter space includes:

