
De Finetti's theorem
Encyclopedia
In probability theory
, de Finetti's theorem explains why exchangeable observations are conditionally independent given some latent variable
to which an epistemic probability distribution
would then be assigned. It is named in honor of Bruno de Finetti
.
It states that an exchangeable sequence of Bernoulli random variables is a "mixture" of independent and identically distributed (i.i.d.) Bernoulli random variables – while the individual variables of the exchangeable sequence are not themselves i.i.d., only exchangeable, there is an underlying family of i.i.d. random variables.
Thus, while observations need not be i.i.d. for a sequence to be exchangeable, there are underlying, generally unobservable, quantities which are i.i.d. – exchangeable sequences are (not necessarily i.i.d.) mixtures of i.i.d. sequences.
An infinite sequence
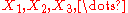
of random variables is said to be exchangeable if for any finite cardinal number
n and any two finite sequences i1, ..., in and j1, ..., jn (with each of the is distinct, and each of the js distinct), the two sequences

both have the same joint probability distribution.
If an identically distributed sequence is independent
, then the sequence is exchangeable; however, the converse is false --- there exist exchangeable random variables that are statistically dependent, for example the Polya urn model
.
X has a Bernoulli distribution if Pr(X = 1) = p and Pr(X = 0) = 1 − p for some p ∈ (0, 1).
De Finetti's theorem states that the probability distribution of any infinite exchangeable sequence of Bernoulli random variables is a "mixture" of the probability distributions of independent and identically distributed sequences of Bernoulli random variables. "Mixture", in this sense, means a weighted average, but this need not mean a finite or countably infinite (i.e., discrete) weighted average: it can be an integral rather than a sum.
More precisely, suppose X1, X2, X3, ... is an infinite exchangeable sequence of Bernoulli-distributed random variables. Then there is some probability distribution m on the interval [0, 1] and some random variable Y such that
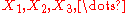
given the event that p = 2/3, is described by saying that they are independent and identically distributed and X1 = 1 with probability 2/3 and X1 = 0 with probability 1 − (2/3). Further, the conditional distribution of the same sequence given the event that p = 9/10, is described by saying that they are independent and identically distributed and X1 = 1 with probability 9/10 and X1 = 0 with probability 1 − (9/10). The independence asserted here is conditional independence, i.e., the Bernoulli random variables in the sequence are conditionally independent given the event that p = 2/3, and are conditionally independent given the event that p = 9/10. But they are not unconditionally independent; they are positively correlated
. In view of the strong law of large numbers
, we can say that
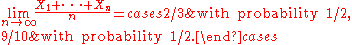
Rather than concentrating probability 1/2 at each of two points between 0 and 1, the "mixing distribution" can be any probability distribution
supported on the interval from 0 to 1; which one it is depends on the joint distribution of the infinite sequence of Bernoulli random variables.
The conclusion of the first version of the theorem above makes sense if the sequence of exchangeable Bernoulli random variables is finite, but the theorem is not generally true in that case. It is true if the sequence can be extended to an exchangeable sequence that is infinitely long. The simplest example of an exchangeable sequence of Bernoulli random variables that cannot be so extended is the one in which X1 = 1 − X2 and X1 is either 0 or 1, each with probability 1/2. This sequence is exchangeable, but cannot be extended to an exchangeable sequence of length 3, let alone an infinitely long one.
Two notions of partial exchangeability of arrays, known as separate and joint exchangeability lead to extensions of de Finetti's theorem for arrays by Aldous and Hoover.
The computable de Finetti theorem shows that if an exchangeable sequence of real random variables is given by a computer program, then a program which samples from the mixing measure can be automatically recovered.
In the setting of free probability
, there is a noncommutative extension of de Finetti's theorem which characterizes noncommutative sequences invariant under quantum permutations.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, de Finetti's theorem explains why exchangeable observations are conditionally independent given some latent variable
Latent variable
In statistics, latent variables , are variables that are not directly observed but are rather inferred from other variables that are observed . Mathematical models that aim to explain observed variables in terms of latent variables are called latent variable models...
to which an epistemic probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
would then be assigned. It is named in honor of Bruno de Finetti
Bruno de Finetti
Bruno de Finetti was an Italian probabilist, statistician and actuary, noted for the "operational subjective" conception of probability...
.
It states that an exchangeable sequence of Bernoulli random variables is a "mixture" of independent and identically distributed (i.i.d.) Bernoulli random variables – while the individual variables of the exchangeable sequence are not themselves i.i.d., only exchangeable, there is an underlying family of i.i.d. random variables.
Thus, while observations need not be i.i.d. for a sequence to be exchangeable, there are underlying, generally unobservable, quantities which are i.i.d. – exchangeable sequences are (not necessarily i.i.d.) mixtures of i.i.d. sequences.
Background
A Bayesian statistician often seeks the conditional probability distribution of a random quantity given the data. The concept of exchangeability was introduced by de Finetti. De Finetti's theorem explains a mathematical relationship between independence and exchangeability.An infinite sequence
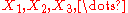
of random variables is said to be exchangeable if for any finite cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
n and any two finite sequences i1, ..., in and j1, ..., jn (with each of the is distinct, and each of the js distinct), the two sequences

both have the same joint probability distribution.
If an identically distributed sequence is independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
, then the sequence is exchangeable; however, the converse is false --- there exist exchangeable random variables that are statistically dependent, for example the Polya urn model
Polya urn model
In statistics, a Polya urn model , named after George Pólya, is a type of statistical model used as an idealized mental exercise to understand the nature of certain statistical distributions.In an urn model, objects of real interest are represented as colored balls in an urn or...
.
Statement of the theorem
A random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X has a Bernoulli distribution if Pr(X = 1) = p and Pr(X = 0) = 1 − p for some p ∈ (0, 1).
De Finetti's theorem states that the probability distribution of any infinite exchangeable sequence of Bernoulli random variables is a "mixture" of the probability distributions of independent and identically distributed sequences of Bernoulli random variables. "Mixture", in this sense, means a weighted average, but this need not mean a finite or countably infinite (i.e., discrete) weighted average: it can be an integral rather than a sum.
More precisely, suppose X1, X2, X3, ... is an infinite exchangeable sequence of Bernoulli-distributed random variables. Then there is some probability distribution m on the interval [0, 1] and some random variable Y such that
- The probability distribution of Y is m, and
- The conditional probability distribution of the whole sequence X1, X2, X3, ... given the value of Y is described by saying that
- X1, X2, X3, ... are conditionally independentConditional independenceIn probability theory, two events R and B are conditionally independent given a third event Y precisely if the occurrence or non-occurrence of R and the occurrence or non-occurrence of B are independent events in their conditional probability distribution given Y...
given Y, and - For any i ∈ {1, 2, 3, ...}, the conditional probability that Xi = 1, given the value of Y, is Y.
- X1, X2, X3, ... are conditionally independent
Another way of stating the theorem
Suppose X1, X2, X3, ... is an infinite exchangeable sequence of Bernoulli-distributed random variables. Then X1, X2, X3, ... are conditionally independent given the tail sigma-field.Example
Here is a concrete example. Suppose p = 2/3 with probability 1/2 and p = 9/10 with probability 1/2. Suppose the conditional distribution of the sequence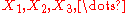
given the event that p = 2/3, is described by saying that they are independent and identically distributed and X1 = 1 with probability 2/3 and X1 = 0 with probability 1 − (2/3). Further, the conditional distribution of the same sequence given the event that p = 9/10, is described by saying that they are independent and identically distributed and X1 = 1 with probability 9/10 and X1 = 0 with probability 1 − (9/10). The independence asserted here is conditional independence, i.e., the Bernoulli random variables in the sequence are conditionally independent given the event that p = 2/3, and are conditionally independent given the event that p = 9/10. But they are not unconditionally independent; they are positively correlated
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
. In view of the strong law of large numbers
Law of large numbers
In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
, we can say that
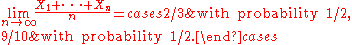
Rather than concentrating probability 1/2 at each of two points between 0 and 1, the "mixing distribution" can be any probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
supported on the interval from 0 to 1; which one it is depends on the joint distribution of the infinite sequence of Bernoulli random variables.
The conclusion of the first version of the theorem above makes sense if the sequence of exchangeable Bernoulli random variables is finite, but the theorem is not generally true in that case. It is true if the sequence can be extended to an exchangeable sequence that is infinitely long. The simplest example of an exchangeable sequence of Bernoulli random variables that cannot be so extended is the one in which X1 = 1 − X2 and X1 is either 0 or 1, each with probability 1/2. This sequence is exchangeable, but cannot be extended to an exchangeable sequence of length 3, let alone an infinitely long one.
Extensions
Versions of de Finetti's theorem for finitely exchangeable sequences and for Markov exchangeable sequences have been proved by Diaconis and Freedman.Two notions of partial exchangeability of arrays, known as separate and joint exchangeability lead to extensions of de Finetti's theorem for arrays by Aldous and Hoover.
The computable de Finetti theorem shows that if an exchangeable sequence of real random variables is given by a computer program, then a program which samples from the mixing measure can be automatically recovered.
In the setting of free probability
Free probability
Free probability is a mathematical theory that studies non-commutative random variables. The "freeness" or free independence property is the analogue of the classical notion of independence, and it is connected with free products....
, there is a noncommutative extension of de Finetti's theorem which characterizes noncommutative sequences invariant under quantum permutations.

