
De Branges' theorem
Encyclopedia
In complex analysis
, the Bieberbach conjecture or de Branges's theorem, posed by and proven by , states a necessary condition on a holomorphic function
to map the open unit disk of the complex plane
injectively to the complex plane.
The statement concerns the Taylor coefficient
s an of such a function, normalized as is always possible so that a0 = 0 and a1 = 1. That is, we consider a holomorphic function
of the form

which is defined and injective on the open unit disk (such functions are also called univalent or schlicht functions). The theorem then states that
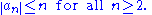
mean that
this can always be assured by a linear fractional transformation: starting with an arbitrary injective holomorphic function g defined on the open unit disk and setting
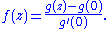
Such functions g are of interest because they appear in the Riemann mapping theorem.
A family of schlicht functions are the rotated Köbe functions
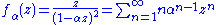
with α a complex number of absolute value
1. If f is a schlicht function and |an| = n for some n ≥ 2, then f is a rotated Köbe function.
The condition of de Branges' theorem is not sufficient to show the function is schlicht, as the function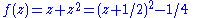
shows: it is holomorphic on the unit disc and satisfies |an|≤n for all n, but it is not injective since f(−1/2 + z) = f(−1/2 − z).
proved |a3| ≤ 3, using the Löwner equation. His work was used by most later attempts, and is also applied in the theory of Schramm–Loewner evolution.
proved that |an| ≤ en for all n, showing that the Bieberbach conjecture is true up to a factor of e = 2.718... Several authors later reduced the constant in the inequality below e.
If f(z) = z + ... is a schlicht function then φ(z) = f(z2)1/2 is an odd schlicht function.
showed that bk ≤ 14 for all k. They conjectured that 14 can be replaced by 1 as a natural generalization of the Bieberbach conjecture. The Littlewood–Paley conjecture easily implies the Bieberbach conjecture using the Cauchy inequality, but it was soon disproved by , who showed there is an odd schlicht function with b5 = 1/2 + exp(−2/3) = 1.013..., and that this is the maximum possible value of b5. (Milin
later showed that 14 can be replaced by 1.14., and Hayman showed that the numbers bk have a limit less than 1 if φ is not a Koebe function, so Littewood and Paley's conjecture is true for all but a finite number of coefficients of any function.) A weaker form of Littlewood and Paley's conjecture was found by .
The Robertson conjecture states that if

is an odd schlicht function in the unit disk with b1=1 then for all positive integers n,
Robertson observed that his conjecture is still strong enough to imply the Bieberbach conjecture, and proved it for n = 3. This conjecture introduced the key idea of bounding various quadratic functions of the coefficients rather than the coefficients themselves, which is equivalent to bounding norms of elements in certain Hilbert spaces of schlicht functions.
There were several proofs of the Bieberbach conjecture for certain higher values of n, in particular proved |a4| ≤ 4, and proved |a6| ≤ 6, and proved |a5| ≤ 5.
proved that the limit of an/n exists, and has absolute value less than 1 unless f is a Koebe function. In particular this showed that for any f there can be at most a finite number of exceptions to the Bieberbach conjecture.
The Milin conjecture states that for each simple function on the unit disk, and for all positive integers n,
where the logarithmic coefficients γn of f are given by

showed using the Lebedev–Milin inequality
that the Milin conjecture (later proved by de Branges) implies the Robertson conjecture and therefore the Bieberbach conjecture.
Finally proved |an| ≤ n for all n.
s of entire function
s. The study of these spaces grew into a sub-field of complex analysis and the spaces come to be called de Branges space
s and the functions de Branges functions. De Branges proved the stronger Milin conjecture on logarithmic coefficients. This was already known to imply the Robertson conjecture about odd univalent functions, which in turn was known to imply the Bieberbach conjecture about simple functions . His proof uses the Loewner equation, the Askey–Gasper inequality
about Jacobi polynomials, and the Lebedev–Milin inequality
on exponentiated power series.
De Branges reduced the conjecture to some inequalities for Jacobi polynomials, and verified the first few by hand. Walter Gautschi verified more of these inequalities by computer for de Branges (proving the Bieberbach conjecture for the first 30 or so coefficients) and then asked Richard Askey if he knew of any similar inequalities. Askey pointed out that had proved the necessary inequalities eight years before, which allowed de Branges to complete his proof. The first version was very long and had some minor mistakes which caused some skepticism about it, but these were corrected with the help of members of the Leningrad Department of Steklov Mathematical Institute
when de Branges visited in 1984.
De Branges proved the following result, which for ν = 0 implies the Milin conjecture (and therefore the Bieberbach conjecture).
Suppose that ν > −3/2 and σn are real numbers for positive integers n with limit 0 and such that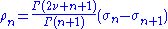
is non-negative, non-increasing, and has limit 0. Then for all Riemann mapping functions F(z) = z + ... univalent in the unit disk with
the maximinum value of
is achieved by the Koebe function z/(1 − z)2.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, the Bieberbach conjecture or de Branges's theorem, posed by and proven by , states a necessary condition on a holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
to map the open unit disk of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
injectively to the complex plane.
The statement concerns the Taylor coefficient
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
s an of such a function, normalized as is always possible so that a0 = 0 and a1 = 1. That is, we consider a holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
of the form

which is defined and injective on the open unit disk (such functions are also called univalent or schlicht functions). The theorem then states that
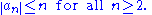
Schlicht functions
The normalizations- a0 = 0 and a1 = 1
mean that
- f(0) = 0 and f '(0) = 1;
this can always be assured by a linear fractional transformation: starting with an arbitrary injective holomorphic function g defined on the open unit disk and setting
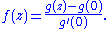
Such functions g are of interest because they appear in the Riemann mapping theorem.
A family of schlicht functions are the rotated Köbe functions
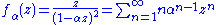
with α a complex number of absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
1. If f is a schlicht function and |an| = n for some n ≥ 2, then f is a rotated Köbe function.
The condition of de Branges' theorem is not sufficient to show the function is schlicht, as the function
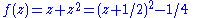
shows: it is holomorphic on the unit disc and satisfies |an|≤n for all n, but it is not injective since f(−1/2 + z) = f(−1/2 − z).
History
proved |a2| ≤ 2, and stated the conjecture that |an| ≤ n. Then Charles LoewnerCharles Loewner
Charles Loewner was an American mathematician. His name was Karel Löwner in Czech and Karl Löwner in German.Loewner received his Ph.D...
proved |a3| ≤ 3, using the Löwner equation. His work was used by most later attempts, and is also applied in the theory of Schramm–Loewner evolution.
proved that |an| ≤ en for all n, showing that the Bieberbach conjecture is true up to a factor of e = 2.718... Several authors later reduced the constant in the inequality below e.
If f(z) = z + ... is a schlicht function then φ(z) = f(z2)1/2 is an odd schlicht function.
showed that bk ≤ 14 for all k. They conjectured that 14 can be replaced by 1 as a natural generalization of the Bieberbach conjecture. The Littlewood–Paley conjecture easily implies the Bieberbach conjecture using the Cauchy inequality, but it was soon disproved by , who showed there is an odd schlicht function with b5 = 1/2 + exp(−2/3) = 1.013..., and that this is the maximum possible value of b5. (Milin
Isaak Moiseevich Milin
Isaak Moiseevich Milin was a Russian mathematician who worked on coefficients of univalent and meromorphic functions. He found the Lebedev-Milin inequality, and stated the Milin conjecture that played an important role in the proof of the Bieberbach conjecture....
later showed that 14 can be replaced by 1.14., and Hayman showed that the numbers bk have a limit less than 1 if φ is not a Koebe function, so Littewood and Paley's conjecture is true for all but a finite number of coefficients of any function.) A weaker form of Littlewood and Paley's conjecture was found by .
The Robertson conjecture states that if

is an odd schlicht function in the unit disk with b1=1 then for all positive integers n,

Robertson observed that his conjecture is still strong enough to imply the Bieberbach conjecture, and proved it for n = 3. This conjecture introduced the key idea of bounding various quadratic functions of the coefficients rather than the coefficients themselves, which is equivalent to bounding norms of elements in certain Hilbert spaces of schlicht functions.
There were several proofs of the Bieberbach conjecture for certain higher values of n, in particular proved |a4| ≤ 4, and proved |a6| ≤ 6, and proved |a5| ≤ 5.
proved that the limit of an/n exists, and has absolute value less than 1 unless f is a Koebe function. In particular this showed that for any f there can be at most a finite number of exceptions to the Bieberbach conjecture.
The Milin conjecture states that for each simple function on the unit disk, and for all positive integers n,

where the logarithmic coefficients γn of f are given by

showed using the Lebedev–Milin inequality
Lebedev–Milin inequality
In mathematics, the Lebedev–Milin inequality is any of several inequalities for the coefficients of the exponential of a power series, found by and...
that the Milin conjecture (later proved by de Branges) implies the Robertson conjecture and therefore the Bieberbach conjecture.
Finally proved |an| ≤ n for all n.
De Branges's proof
The proof uses a type of Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s of entire function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
s. The study of these spaces grew into a sub-field of complex analysis and the spaces come to be called de Branges space
De Branges space
In mathematics, a de Branges space is a concept in functional analysis and is constructed from a de Branges function....
s and the functions de Branges functions. De Branges proved the stronger Milin conjecture on logarithmic coefficients. This was already known to imply the Robertson conjecture about odd univalent functions, which in turn was known to imply the Bieberbach conjecture about simple functions . His proof uses the Loewner equation, the Askey–Gasper inequality
Askey–Gasper inequality
In mathematics, the Askey–Gasper inequality is an inequality for Jacobi polynomials proved by and used in the proof of the Bieberbach conjecture.-Statement:...
about Jacobi polynomials, and the Lebedev–Milin inequality
Lebedev–Milin inequality
In mathematics, the Lebedev–Milin inequality is any of several inequalities for the coefficients of the exponential of a power series, found by and...
on exponentiated power series.
De Branges reduced the conjecture to some inequalities for Jacobi polynomials, and verified the first few by hand. Walter Gautschi verified more of these inequalities by computer for de Branges (proving the Bieberbach conjecture for the first 30 or so coefficients) and then asked Richard Askey if he knew of any similar inequalities. Askey pointed out that had proved the necessary inequalities eight years before, which allowed de Branges to complete his proof. The first version was very long and had some minor mistakes which caused some skepticism about it, but these were corrected with the help of members of the Leningrad Department of Steklov Mathematical Institute
St. Petersburg Department of Steklov Institute of Mathematics of Russian Academy of Sciences
The St. Petersburg Department of Steklov Institute of Mathematics of Russian Academy of Sciences for "Петербургское отделение Математического института", Petersburg Department of the Mathematical Institute) is a mathematical research institute in St. Petersburg, part of the Russian Academy of...
when de Branges visited in 1984.
De Branges proved the following result, which for ν = 0 implies the Milin conjecture (and therefore the Bieberbach conjecture).
Suppose that ν > −3/2 and σn are real numbers for positive integers n with limit 0 and such that
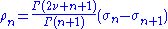
is non-negative, non-increasing, and has limit 0. Then for all Riemann mapping functions F(z) = z + ... univalent in the unit disk with

the maximinum value of

is achieved by the Koebe function z/(1 − z)2.

