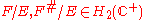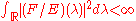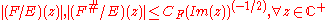De Branges space
Encyclopedia
In mathematics
, a de Branges space (sometimes written De Branges space) is a concept in functional analysis
and is constructed from a de Branges function.
The concept is named after Louis de Branges who proved numerous results regarding these spaces, especially as Hilbert space
s, and used those results to prove the Bieberbach conjecture.
E from
to 
that satisfies the inequality 
, for all z in the upper half of the complex plane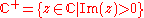 
.
s F such that:
where:
A de Branges space with such a scalar product can be proven to be a Hilbert space.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a de Branges space (sometimes written De Branges space) is a concept in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and is constructed from a de Branges function.
The concept is named after Louis de Branges who proved numerous results regarding these spaces, especially as Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s, and used those results to prove the Bieberbach conjecture.
De Branges functions
A de Branges function is an entire functionEntire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
E from
to that satisfies the inequality , for all z in the upper half of the complex plane 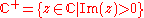.Definition 1
Given a de Branges function E, the de Branges space B(E) is defined as the set of all entire functionEntire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
s F such that:
where:
-
is the open upper half of the complex plane. -
. -
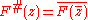is the usual Hardy spaceHardy spaceIn complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
on the open upper half plane.
Definition 2
A de Branges space can also be defined as all entire functions F satisfying all of the following conditions:
As Hilbert spaces
Given a de Branges space B(E). Define the scalar product:A de Branges space with such a scalar product can be proven to be a Hilbert space.