Dagger compact category
Encyclopedia
In mathematics, dagger compact categories (or dagger compact closed categories) first appeared in 1989 in the work of Doplicher and Roberts on the reconstruction of compact topological group from their category of finite-dimensional continuous unitary representations. They also appeared independently in the work of Baez and Dolan as an instance of semistrict k-tuply monoidal n-categories, which describe general topological quantum field theories, for n = 1 and k = 3.
Selinger showed that dagger compact categories admit a Joyal-Street style diagrammatic language and proved that dagger compact categories are complete with respect to finite dimensional Hilbert spaces i.e. an equational statement in the language of dagger compact categories holds if and only if it can be derived in the concrete category of finite dimensional Hilbert spaces and linear maps.
, logic gate teleportation and entanglement swapping
; the resulting line of research is now known as categorical quantum mechanics
.
, a dagger compact category is a dagger symmetric monoidal category which is also compact closed
which is also compact closed
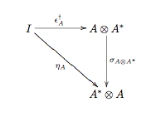
and such that for all in
in  ,
,
 commutes.
commutes.
Selinger showed that dagger compact categories admit a Joyal-Street style diagrammatic language and proved that dagger compact categories are complete with respect to finite dimensional Hilbert spaces i.e. an equational statement in the language of dagger compact categories holds if and only if it can be derived in the concrete category of finite dimensional Hilbert spaces and linear maps.
Connection to quantum information processing
Dagger compact categories were applied to capture some quantum information protocols namely: teleportationQuantum teleportation
Quantum teleportation, or entanglement-assisted teleportation, is a process by which a qubit can be transmitted exactly from one location to another, without the qubit being transmitted through the intervening space...
, logic gate teleportation and entanglement swapping
Quantum teleportation
Quantum teleportation, or entanglement-assisted teleportation, is a process by which a qubit can be transmitted exactly from one location to another, without the qubit being transmitted through the intervening space...
; the resulting line of research is now known as categorical quantum mechanics
Categorical quantum mechanics
Categorical quantum mechanics is the study of quantum physics using methods from mathematics and computer science, notably category theory, that emphasize compositionality...
.
Formal definition
In mathematicsMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a dagger compact category is a dagger symmetric monoidal category
 which is also compact closed
which is also compact closedCompact closed category
In category theory, compact closed categories are a general context for treating dual objects. The idea of a dual object generalizes the more familiar concept of the dual of a finite-dimensional vector space...
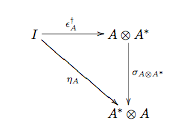
and such that for all
 in
in  ,
,
Examples
The following categories are dagger compact.- The category FdHilb of finite dimensional Hilbert spacesCategory of finite dimensional Hilbert spacesIn mathematics, the category FdHilb has all finite dimensional Hilbert spaces for objects and linear transformations between them.-Properties:This category* is monoidal,* possesses finite biproducts, and* is dagger compact....
and linear maps. - The category Rel of Sets and relationsCategory of relationsIn mathematics, the category Rel has the class of sets as objects and binary relations as morphisms.A morphism R : A → B in this category is a relation between the sets A and B, so ....
. - The category of finitely generatedFinitely generatedIn mathematics, finitely generated may refer to:* Finitely generated group* Finitely generated monoid* Finitely generated abelian group* Finitely generated module* Finitely generated ideal* Finitely generated algebra* Finitely generated space...
projective modules over a commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
.

