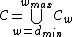DNA code construction
Encyclopedia
DNA code construction refers to the application of coding theory
to the design
of nucleic acid systems for the field of DNA–based computation
.
sequences are known to appear in the form of double helices
in living cells
, in which one DNA strand is hybridized
to its complementary
strand through a series of hydrogen bond
s. For the purpose of this entry, we shall focus on only oligonucleotide
s. DNA computing
involves allowing synthetic
oligonucleotide strands to hybridize in such a way as to perform computation
. DNA computing requires that the self-assembly of the oligonucleotide strands happen in such a way that hybridization should occur in a manner compatible with the goals of computation.
The field of DNA computing was established in Leonard M. Adelman’s seminal paper. His work is significant for a number of reasons:
This capability for massively parallel computation
in DNA computing can be exploited in solving many computational problems on an enormously large scale such as cell-based computational systems for cancer diagnostics and treatment, and ultra-high density storage media.
This selection of codewords (sequences of DNA oligonucleotides) is a major hurdle in itself due to the phenomenon of secondary structure formation (in which DNA strands tend to fold onto themselves during hybridization and hence rendering themselves useless in further computations. This is also known as self-hybridization). The Nussinov-Jacobson algorithm is used to predict secondary structures and also to identify certain design criteria that reduce the possibility of secondary structure formation in a codeword. In essence this algorithm shows how the presence of a cyclic structure in a DNA code reduces the complexity of the problem of testing the codewords for secondary structures.
Novel constructions of such codes include using cyclic reversible extended Goppa codes, generalized Hadamard matrices
, and a binary approach. Before diving into these constructions, we shall revisit certain fundamental genetic terminology. The motivation for the theorems presented in this article, is that they concur with the Nussinov - Jacobson algorithm, in that the existence of cyclic structure helps in reducing complexity and thus prevents secondary structure formation. i.e. these algorithms satisfy some or all the design requirements for DNA oligonucleotides at the time of hybridization (which is the core of the DNA computing process) and hence do not suffer from the problems of self - hybridization.
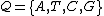 .
.
Each purine
base is the Watson-Crick complement
of a unique pyrimidine
base (and vice versa) – adenine
and thymine
form a complementary pair, as do guanine
and cytosine
. This pairing can be described as follows –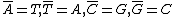 .
.
Such pairing is chemically very stable and strong. However, pairing of mismatching bases does occur at times due to biological mutations.
Most of the focus on DNA coding has been on constructing large sets of DNA codewords with prescribed minimum distance properties.
For this purpose let us lay down the required groundwork to proceed further.
Let be a word of length
be a word of length  over the alphabet
over the alphabet  . For
. For  , we will use the notation
, we will use the notation  to denote the subsequence
to denote the subsequence 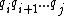 . Furthermore, the sequence obtained by reversing
. Furthermore, the sequence obtained by reversing 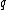 will be denoted as
will be denoted as 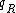 . The Watson-Crick complement, or the reverse-complement of q, is defined to be
. The Watson-Crick complement, or the reverse-complement of q, is defined to be 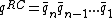 , where
, where 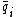 denotes the Watson-Crick complement base pair of
denotes the Watson-Crick complement base pair of 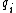 .
.
For any pair of length- words
words 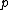 and
and 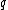 over
over 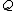 , the Hamming distance
, the Hamming distance
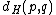 is the number of positions
is the number of positions 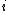 at which
at which 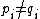 . Further, define reverse-Hamming distance as
. Further, define reverse-Hamming distance as 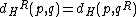 . Similarly, reverse-complement Hamming distance is
. Similarly, reverse-complement Hamming distance is 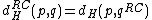 . (where
. (where 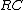 stands for reverse complement)
stands for reverse complement)
Another important code design consideration linked to the process of oligonucleotide hybridization pertains to the GC content of sequences in a DNA code. The GC-content,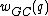 , of a DNA sequence
, of a DNA sequence 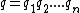 is defined to be the number of indices
is defined to be the number of indices 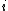 such that
such that 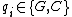 . A DNA code in which all codewords have the same GC-content,
. A DNA code in which all codewords have the same GC-content, 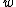 , is called a constant GC-content code.
, is called a constant GC-content code.
A generalized Hadamard matrix
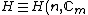 ) is an
) is an 

 square matrix with entries taken from the set of
square matrix with entries taken from the set of 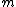 th roots of unity,
th roots of unity, 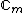 =
= 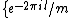 ,
,  = 0, ...,
= 0, ..., 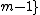 , that satisfies
, that satisfies  =
= 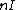 . Here
. Here  denotes the identity matrix of order
denotes the identity matrix of order  , while * stands for complex-congugation. We will only concern ourselves with the case
, while * stands for complex-congugation. We will only concern ourselves with the case 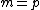 for some prime
for some prime 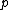 . A necessary condition for the existence of generalized Hadamard matrices
. A necessary condition for the existence of generalized Hadamard matrices 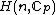 is that
is that 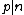 . The exponent matrix,
. The exponent matrix, 
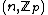 , of
, of 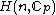 is the
is the 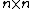 matrix with the entries in
matrix with the entries in  , is obtained by replacing each entry
, is obtained by replacing each entry 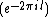 in
in 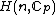 by the exponent
by the exponent  .
.
The elements of the Hadamard exponent matrix lie in the Galois field
 , and its row vectors constitute the codewords of what shall be called a generalized Hadamard code.
, and its row vectors constitute the codewords of what shall be called a generalized Hadamard code.
Here, the elements of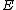 lie in the Galois field
lie in the Galois field 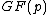 .
.
By definition, a generalized Hadamard matrix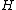 in its standard form has only 1s in its first row and column. The
in its standard form has only 1s in its first row and column. The 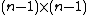 square matrix formed by the remaining entries of
square matrix formed by the remaining entries of 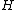 is called the core of
is called the core of 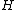 , and the corresponding submatrix of the exponent matrix
, and the corresponding submatrix of the exponent matrix  is called the core of construction. Thus, by omission of the all-zero first column cyclic generalized Hadamard codes are possible,
is called the core of construction. Thus, by omission of the all-zero first column cyclic generalized Hadamard codes are possible,
whose codewords are the row vectors of the punctured matrix.
Also, the rows of such an exponent matrix satisfy the following two properties: (i) in each of the nonzero rows of the exponent matrix, each element of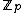 appears a constant number,
appears a constant number, 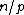 , of times; and (ii) the Hamming distance between any two rows is
, of times; and (ii) the Hamming distance between any two rows is 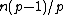 .
.
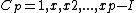 be the cyclic group generated by
be the cyclic group generated by  , where
, where 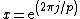 is a complex primitive
is a complex primitive 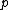 th root of unity, and
th root of unity, and 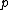 >
> 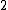 is a fixed prime. Further, let
is a fixed prime. Further, let 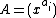 ,
, 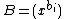 denote arbitrary vectors over
denote arbitrary vectors over 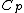 which are of length
which are of length  , where
, where  is a positive integer. Define the collection of differences between exponents
is a positive integer. Define the collection of differences between exponents  , where
, where 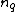 is the multiplicity of element
is the multiplicity of element  of
of  which appears in
which appears in 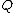 .
.
Vector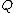 is said to satisfy Property U iff each element
is said to satisfy Property U iff each element 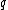 of
of 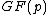 appears in
appears in 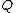 exactly
exactly  times (
times (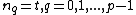 )
)
The following lemma is of fundamental importance in constructing generalized Hadamard codes.
Lemma. Orthogonality of vectors over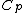 - For fixed primes
- For fixed primes 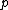 , arbitrary vectors
, arbitrary vectors 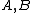 of length
of length 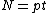 , whose elements are from
, whose elements are from  , are orthogonal if the vector
, are orthogonal if the vector 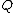 satisfies Property U, where
satisfies Property U, where  is the collection of
is the collection of  differences between the Hadamard exponents associated with
differences between the Hadamard exponents associated with 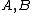 .
.
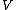 be an arbitrary vector of length
be an arbitrary vector of length 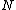 whose elements are in the finite field
whose elements are in the finite field 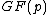 , where
, where  is a prime. Let the elements of vector
is a prime. Let the elements of vector  constitute the first period of an infinite sequence
constitute the first period of an infinite sequence  which is periodic of period
which is periodic of period 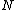 . If
. If 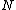 is the smallest period for conceiving a subsequence, the sequence is called an M-sequence, or a sequence of maximal least period obtained by cycling
is the smallest period for conceiving a subsequence, the sequence is called an M-sequence, or a sequence of maximal least period obtained by cycling 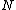 elements. If, when the elements of the ordered set
elements. If, when the elements of the ordered set  are permuted arbitrarily to yield
are permuted arbitrarily to yield 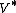 , the sequence
, the sequence  is an M-sequence, the sequence
is an M-sequence, the sequence  is called M-invariant.
is called M-invariant.
The theorems that follow present conditions that ensure invariance in an M sequence. In conjunction with a certain uniformity property of
polynomial coeffecients, these conditions yield a simple method by which complex Hadamard matrices with cyclic core can be constructed.
The goal as outlined at the head of this article is to find cyclic matrix whose elements are in Galois field
whose elements are in Galois field 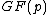 and whose dimension is
and whose dimension is 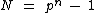 . The rows of
. The rows of 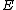 will be the nonzero codewords of a linear cyclic code
will be the nonzero codewords of a linear cyclic code 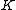 , if and only if there is polynomial
, if and only if there is polynomial 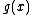 with coefficients in
with coefficients in 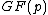 , which is a proper divisor of
, which is a proper divisor of  and which generates
and which generates 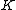 .
.
In order to have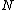 nonzero codewords,
nonzero codewords, 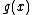 must be of degree
must be of degree 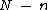 . Further, in order to generate a cyclic Hadamard core, the vector (of coefficients of)
. Further, in order to generate a cyclic Hadamard core, the vector (of coefficients of) 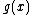 when operated upon with the cyclic shift operation must be of period
when operated upon with the cyclic shift operation must be of period 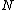 , and the vector difference of two arbitrary rows of
, and the vector difference of two arbitrary rows of 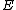 (augmented with zero) must satisfy the uniformity condition of Butson, previously referred to as Property U.
(augmented with zero) must satisfy the uniformity condition of Butson, previously referred to as Property U.
One necessary condition for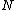 -peridoicity is that
-peridoicity is that 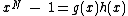 , where
, where  is monic irreducible
is monic irreducible
over.
The approach here is to replace the last requirement with the condition that the coefficients of the vector be uniformly distributed over
be uniformly distributed over 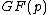 , each residue
, each residue  appears the same number of times (Property U). This heuristic approach has succeeded for all cases tried, and a proof that it always produces a cyclic core is given below.
appears the same number of times (Property U). This heuristic approach has succeeded for all cases tried, and a proof that it always produces a cyclic core is given below.
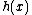 over
over 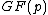 which are of degree
which are of degree  , and which permit a suitable companion
, and which permit a suitable companion 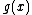 of degree
of degree 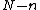 such that
such that 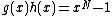 , where also vector
, where also vector 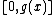 satisfies Property U. This requires only a simple computer algorithm for long division over
satisfies Property U. This requires only a simple computer algorithm for long division over 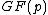 . Since
. Since 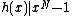 , the ideal generated by
, the ideal generated by 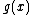 ,
, 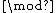
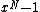 , will be a cyclic code
, will be a cyclic code 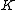 . Moreover, Property U guarantees the nonzero codewords form a cyclic matrix, each row being of period
. Moreover, Property U guarantees the nonzero codewords form a cyclic matrix, each row being of period 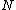 under cyclic permutation, which serves as a cyclic core
under cyclic permutation, which serves as a cyclic core
for Hadamard matrix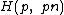 .
.
As an example, a cyclic core for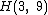 results from the companions
results from the companions 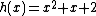 and
and 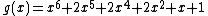 . The coefficients of
. The coefficients of 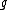 indicate that
indicate that 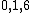 is the relative difference set,
is the relative difference set, 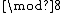 .
.
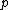 be a prime and
be a prime and 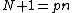 , with
, with 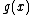 a monic polynomial of degree
a monic polynomial of degree 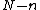 whose extended vector of coefficients
whose extended vector of coefficients 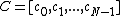 are elements of
are elements of  . The conditions are as follows:
. The conditions are as follows:
(1) vector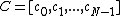 satisfies the property U explained above,
satisfies the property U explained above,
(2)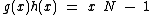 , where
, where 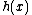 is a monic irreducible polynomial of degree
is a monic irreducible polynomial of degree  , guarantee the existence of a p-ary, linear cyclic code
, guarantee the existence of a p-ary, linear cyclic code 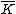 : of blocksize
: of blocksize 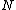 , such that the augmented code
, such that the augmented code 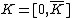 is the Hadamard exponent, for Hadamard matrix
is the Hadamard exponent, for Hadamard matrix 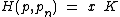 , with
, with 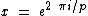 , where the core of
, where the core of 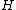 is cyclic matrix.
is cyclic matrix.
Proof:
First, we note that since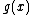 is monic, it divides
is monic, it divides 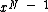 , and has degree =
, and has degree =  . Now, we need to show that the matrix
. Now, we need to show that the matrix  whose rows are the nonzero codewords, constitutes a cyclic core for some complex Hadamard matrix
whose rows are the nonzero codewords, constitutes a cyclic core for some complex Hadamard matrix 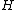 .
.
Given: we know that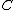 satisfies property U. Hence, all of the nonzero residues of
satisfies property U. Hence, all of the nonzero residues of 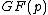 lie in C. By cycling through
lie in C. By cycling through  , we get the desired exponent matrix
, we get the desired exponent matrix 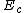 where we can get every codeword in
where we can get every codeword in  by cycling the first codeword. (This is because the sequence obtained by cycling through
by cycling the first codeword. (This is because the sequence obtained by cycling through 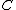 is an M-invariant sequence.)
is an M-invariant sequence.)
We also see that augmentation of each codeword of by adding a leading zero element produces a vector which satisfies Property U. Also, since the code is linear, the
by adding a leading zero element produces a vector which satisfies Property U. Also, since the code is linear, the  vector difference of two arbitrary codewords is also a codeword and thus satisfy Property U. Therefore, the row vectors of the augmented code
vector difference of two arbitrary codewords is also a codeword and thus satisfy Property U. Therefore, the row vectors of the augmented code 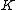 form a Hadamard exponent. Thus,
form a Hadamard exponent. Thus,  is the standard form of some complex Hadamard matrix
is the standard form of some complex Hadamard matrix 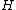 .
.
Thus from the above property, we see that the core of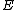 is a circulant matrix
is a circulant matrix
consisting of all the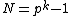 cyclic shifts of its first row. Such a core is called a cyclic core where in each element of
cyclic shifts of its first row. Such a core is called a cyclic core where in each element of 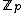 appears in each row of
appears in each row of 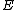 exactly
exactly 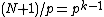 times, and the Hamming distance between any two rows is exactly
times, and the Hamming distance between any two rows is exactly 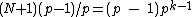 . The
. The 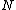 rows of the core
rows of the core 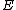 form a constant-composition code - one consisting of
form a constant-composition code - one consisting of  cyclic shifts of some length
cyclic shifts of some length 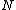 over the set
over the set 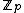 . Hamming distance between any two codewords in
. Hamming distance between any two codewords in 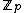 is
is 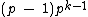 .
.
The following can be inferred from the theorem as explained above. (For more detailed reading, the reader is referred to the paper by Heng and Cooke.)
Let for
for 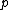 prime and
prime and 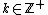 . Let
. Let 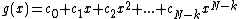 be a monic polynomial over
be a monic polynomial over 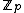 , of degree N - k such that
, of degree N - k such that 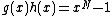 over
over 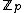 , for some monic irreducible polynomial
, for some monic irreducible polynomial 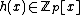 . Suppose that the vector
. Suppose that the vector  , with
, with 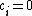 for (N - k) < i < N, has the property that it contains each element of
for (N - k) < i < N, has the property that it contains each element of  the same number of times. Then, the
the same number of times. Then, the 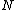 cyclic shifts of the vector
cyclic shifts of the vector 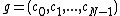 form the core of the exponent matrix of some Hadamard matrix .
form the core of the exponent matrix of some Hadamard matrix .
DNA codes with constant GC-content can obviously be constructed from constant-composition codes (A constant composition code over a k-ary alphabet has the property that the numbers of occurrences of the k symbols within a codeword is the same for each codeword) over by mapping the symbols of
by mapping the symbols of  to the symbols of the DNA alphabet,
to the symbols of the DNA alphabet, 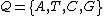 . For example, using cyclic constant composition code of length
. For example, using cyclic constant composition code of length  over
over 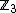 guaranteed by the theorem proved above and the resulting property, and using the mapping that takes
guaranteed by the theorem proved above and the resulting property, and using the mapping that takes 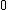 to
to  ,
, 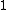 to
to 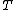 and
and 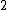 to
to  , we obtain a DNA code
, we obtain a DNA code 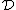 with
with 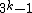 and a GC-content of
and a GC-content of 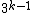 . Clearly
. Clearly 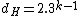 and in fact since
and in fact since 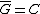 and no codeword in
and no codeword in 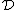 contains no symbol
contains no symbol 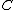 , we also have
, we also have 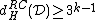 .
.
This is summarized in the following corollary.
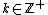 , there exists DNA codes
, there exists DNA codes 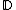 with
with 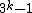 codewords of length
codewords of length  , constant GC-content
, constant GC-content 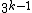 ,
,  and in which every codeword is a cyclic shift of a fixed generator codeword
and in which every codeword is a cyclic shift of a fixed generator codeword 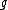 .
.
Each of the following vectors generates a cyclic core of a Hadamard matrix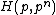 (where
(where 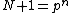 , and
, and 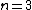 in this example) :
in this example) :
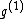 =
= 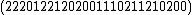 ;
;
 =
= 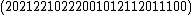 .
.
Where,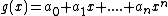 .
.
Thus, we see how DNA codes can be obtained from such generators by mapping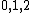 onto
onto 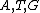 . The actual choice of mapping plays a major role in secondary structure formations in the codewords.
. The actual choice of mapping plays a major role in secondary structure formations in the codewords.
We see that all such mappings yield codes with essentially the same parameters. However the actual choice of mapping has a strong influence on the secondary structure of the codewords. For example, the codeword illustrated was obtained from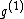 via the mapping
via the mapping 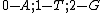 , while the codeword
, while the codeword 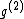 was obtained from the same generator
was obtained from the same generator 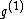 via the mapping
via the mapping 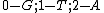 .
.
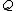 onto the set of 2-bit length binary words as shown:
onto the set of 2-bit length binary words as shown: 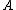 ->
-> 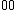 ,
, 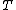 ->
-> 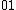 ,
, 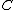 ->
-> 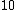 ,
, 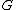 ->
-> .
.
As we can see, the first bit of a binary image clearly determines which complementary pair it belongs to.
Let be a DNA sequence. The sequence
be a DNA sequence. The sequence 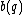 obtained by applying the mapping given above to
obtained by applying the mapping given above to 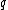 , is called the binary image of
, is called the binary image of 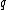 .
.
Now, let =
= 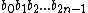 .
.
Now, let the subsequence =
= 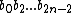 be called the even subsequence of
be called the even subsequence of  , and
, and 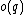 =
= 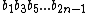 be called the odd subsequence of
be called the odd subsequence of 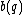 .
.
Thus, for example, for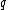 =
= 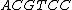 , then,
, then, 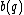 =
= 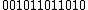 .
.
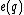 will then be =
will then be = 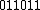 and
and 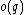 =
=  .
.
Let us define an even component as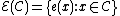 , and an odd component as
, and an odd component as  .
.
From this choice of binary mapping, the GC-content of DNA sequence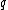 = Hamming weight of
= Hamming weight of 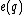 .
.
Hence, a DNA code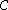 is a constant GC-content codeword if and only if its even component
is a constant GC-content codeword if and only if its even component 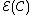 is a constant-weight code.
is a constant-weight code.
Let be a binary code consisting of
be a binary code consisting of 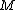 codewords of length
codewords of length  and minimum distance
and minimum distance 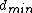 , such that
, such that 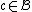 implies that
implies that 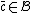 .
.
For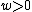 , consider the constant-weight subcode
, consider the constant-weight subcode 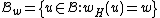 , where
, where 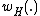 denotes Hamming weight.
denotes Hamming weight.
Choose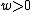 such that
such that 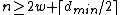 , and consider a DNA code,
, and consider a DNA code, 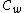 , with the following choice for its even and odd components:
, with the following choice for its even and odd components:
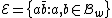 ,
, 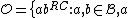 <
<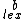
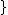 .
.
Where <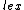 denotes lexicographic ordering. The
denotes lexicographic ordering. The  <
< 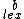 in the definition of
in the definition of 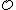 ensures that if
ensures that if 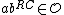 , then
, then 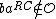 , so that distinct codewords in
, so that distinct codewords in  cannot be reverse-complements of each other.
cannot be reverse-complements of each other.
The code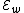 has
has 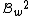 codewords of length
codewords of length 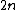 and constant weight
and constant weight  .
.
Furthermore,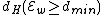 and
and 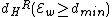 ( this is because
( this is because 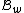 is a subset of the codewords in
is a subset of the codewords in 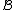 ).
).
Also,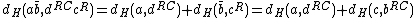 .
.
Note that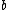 and
and  both have weight
both have weight 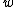 . This implies that
. This implies that 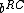 and
and 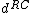 have weight
have weight  .
.
And due to the weight constraint on , we must have for all
, we must have for all 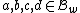 ,
,
 .
.
Thus, the code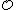 has
has  codewords of length
codewords of length 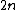 .
.
From this, we see that
(because of the fact that the component codewords of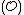 are taken from
are taken from 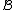 ).
).
Similarly,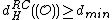 .
.
Therefore, the DNA code
with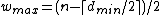 , has
, has 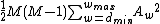 codewords of length
codewords of length  ,
,
and satisfies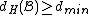
and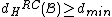 .
.
From the examples listed above, one can wonder what could be the future potential of DNA-based computers?
Despite its enormous potential, this method is highly unlikely to be implemented in home computers or even computers at offices, etc. because of the sheer flexibility and speed as well as cost factors that favor silicon chip based devices used for the computers today.
However, such a method could be used in situations where the only available method is this and requires the accuracy associated with the DNA hybridization mechanism; applications which require operations to be performed with a high degree of reliability.
Currently, there are several software packages, such as the Vienna package, which can predict secondary structure formations in single stranded DNAs (i.e. oligonucleotides) or RNA sequences.
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
to the design
Nucleic acid design
Nucleic acid design is the process of generating a set of nucleic acid base sequences that will associate into a desired conformation. Nucleic acid design is central to the fields of DNA nanotechnology and DNA computing...
of nucleic acid systems for the field of DNA–based computation
DNA computing
DNA computing is a form of computing which uses DNA, biochemistry and molecular biology, instead of the traditional silicon-based computer technologies. DNA computing, or, more generally, biomolecular computing, is a fast developing interdisciplinary area...
.
Introduction
DNADNA
Deoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...
sequences are known to appear in the form of double helices
Nucleic acid double helix
In molecular biology, the term double helix refers to the structure formed by double-stranded molecules of nucleic acids such as DNA and RNA. The double helical structure of a nucleic acid complex arises as a consequence of its secondary structure, and is a fundamental component in determining its...
in living cells
Cell (biology)
The cell is the basic structural and functional unit of all known living organisms. It is the smallest unit of life that is classified as a living thing, and is often called the building block of life. The Alberts text discusses how the "cellular building blocks" move to shape developing embryos....
, in which one DNA strand is hybridized
Nucleic acid thermodynamics
Nucleic acid thermodynamics is the study of the thermodynamics of nucleic acid molecules, or how temperature affects nucleic acid structure. For multiple copies of DNA molecules, the melting temperature is defined as the temperature at which half of the DNA strands are in the double-helical state...
to its complementary
Complementarity (molecular biology)
In molecular biology, complementarity is a property of double-stranded nucleic acids such as DNA, as well as DNA:RNA duplexes. Each strand is complementary to the other in that the base pairs between them are non-covalently connected via two or three hydrogen bonds...
strand through a series of hydrogen bond
Hydrogen bond
A hydrogen bond is the attractive interaction of a hydrogen atom with an electronegative atom, such as nitrogen, oxygen or fluorine, that comes from another molecule or chemical group. The hydrogen must be covalently bonded to another electronegative atom to create the bond...
s. For the purpose of this entry, we shall focus on only oligonucleotide
Oligonucleotide
An oligonucleotide is a short nucleic acid polymer, typically with fifty or fewer bases. Although they can be formed by bond cleavage of longer segments, they are now more commonly synthesized, in a sequence-specific manner, from individual nucleoside phosphoramidites...
s. DNA computing
DNA computing
DNA computing is a form of computing which uses DNA, biochemistry and molecular biology, instead of the traditional silicon-based computer technologies. DNA computing, or, more generally, biomolecular computing, is a fast developing interdisciplinary area...
involves allowing synthetic
Oligonucleotide synthesis
Oligonucleotide synthesis is the chemical synthesis of relatively short fragments of nucleic acids with defined chemical structure . The technique is extremely useful in current laboratory practice because it provides a rapid and inexpensive access to custom-made oligonucleotides of the desired...
oligonucleotide strands to hybridize in such a way as to perform computation
Computation
Computation is defined as any type of calculation. Also defined as use of computer technology in Information processing.Computation is a process following a well-defined model understood and expressed in an algorithm, protocol, network topology, etc...
. DNA computing requires that the self-assembly of the oligonucleotide strands happen in such a way that hybridization should occur in a manner compatible with the goals of computation.
The field of DNA computing was established in Leonard M. Adelman’s seminal paper. His work is significant for a number of reasons:
- It shows how one could use the highly parallel nature of computation performed by DNA to solve problems that are difficult or almost impossible to solve using the traditional methods.
- It's an example of computation at a molecular level, on the lines of nanocomputingNanocomputerNanocomputer is the logical name for a computer smaller than the microcomputer, which is smaller than the minicomputer. More technically, it is a computer whose fundamental parts are no bigger than a few nanometers...
, and this potentially is a major advantage as far as the information density on storage media is considered, which can never be reached by the semiconductor industry.
- It demonstrates unique aspects of DNA as a data structure.
This capability for massively parallel computation
Parallel computing
Parallel computing is a form of computation in which many calculations are carried out simultaneously, operating on the principle that large problems can often be divided into smaller ones, which are then solved concurrently . There are several different forms of parallel computing: bit-level,...
in DNA computing can be exploited in solving many computational problems on an enormously large scale such as cell-based computational systems for cancer diagnostics and treatment, and ultra-high density storage media.
This selection of codewords (sequences of DNA oligonucleotides) is a major hurdle in itself due to the phenomenon of secondary structure formation (in which DNA strands tend to fold onto themselves during hybridization and hence rendering themselves useless in further computations. This is also known as self-hybridization). The Nussinov-Jacobson algorithm is used to predict secondary structures and also to identify certain design criteria that reduce the possibility of secondary structure formation in a codeword. In essence this algorithm shows how the presence of a cyclic structure in a DNA code reduces the complexity of the problem of testing the codewords for secondary structures.
Novel constructions of such codes include using cyclic reversible extended Goppa codes, generalized Hadamard matrices
Hadamard matrix
In mathematics, an Hadamard matrix, named after the French mathematician Jacques Hadamard, is a square matrix whose entries are either +1 or −1 and whose rows are mutually orthogonal...
, and a binary approach. Before diving into these constructions, we shall revisit certain fundamental genetic terminology. The motivation for the theorems presented in this article, is that they concur with the Nussinov - Jacobson algorithm, in that the existence of cyclic structure helps in reducing complexity and thus prevents secondary structure formation. i.e. these algorithms satisfy some or all the design requirements for DNA oligonucleotides at the time of hybridization (which is the core of the DNA computing process) and hence do not suffer from the problems of self - hybridization.
Definitions
A DNA code is simply a set of sequences over the alphabet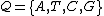 .
.Each purine
Purine
A purine is a heterocyclic aromatic organic compound, consisting of a pyrimidine ring fused to an imidazole ring. Purines, including substituted purines and their tautomers, are the most widely distributed kind of nitrogen-containing heterocycle in nature....
base is the Watson-Crick complement
Base pair
In molecular biology and genetics, the linking between two nitrogenous bases on opposite complementary DNA or certain types of RNA strands that are connected via hydrogen bonds is called a base pair...
of a unique pyrimidine
Pyrimidine
Pyrimidine is a heterocyclic aromatic organic compound similar to benzene and pyridine, containing two nitrogen atoms at positions 1 and 3 of the six-member ring...
base (and vice versa) – adenine
Adenine
Adenine is a nucleobase with a variety of roles in biochemistry including cellular respiration, in the form of both the energy-rich adenosine triphosphate and the cofactors nicotinamide adenine dinucleotide and flavin adenine dinucleotide , and protein synthesis, as a chemical component of DNA...
and thymine
Thymine
Thymine is one of the four nucleobases in the nucleic acid of DNA that are represented by the letters G–C–A–T. The others are adenine, guanine, and cytosine. Thymine is also known as 5-methyluracil, a pyrimidine nucleobase. As the name suggests, thymine may be derived by methylation of uracil at...
form a complementary pair, as do guanine
Guanine
Guanine is one of the four main nucleobases found in the nucleic acids DNA and RNA, the others being adenine, cytosine, and thymine . In DNA, guanine is paired with cytosine. With the formula C5H5N5O, guanine is a derivative of purine, consisting of a fused pyrimidine-imidazole ring system with...
and cytosine
Cytosine
Cytosine is one of the four main bases found in DNA and RNA, along with adenine, guanine, and thymine . It is a pyrimidine derivative, with a heterocyclic aromatic ring and two substituents attached . The nucleoside of cytosine is cytidine...
. This pairing can be described as follows –
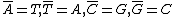 .
.Such pairing is chemically very stable and strong. However, pairing of mismatching bases does occur at times due to biological mutations.
Most of the focus on DNA coding has been on constructing large sets of DNA codewords with prescribed minimum distance properties.
For this purpose let us lay down the required groundwork to proceed further.
Let
 be a word of length
be a word of length  over the alphabet
over the alphabet  . For
. For  , we will use the notation
, we will use the notation  to denote the subsequence
to denote the subsequence 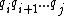 . Furthermore, the sequence obtained by reversing
. Furthermore, the sequence obtained by reversing 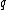 will be denoted as
will be denoted as 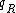 . The Watson-Crick complement, or the reverse-complement of q, is defined to be
. The Watson-Crick complement, or the reverse-complement of q, is defined to be 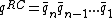 , where
, where 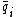 denotes the Watson-Crick complement base pair of
denotes the Watson-Crick complement base pair of 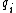 .
.For any pair of length-
 words
words 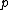 and
and 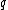 over
over 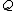 , the Hamming distance
, the Hamming distanceHamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
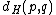 is the number of positions
is the number of positions 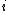 at which
at which 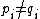 . Further, define reverse-Hamming distance as
. Further, define reverse-Hamming distance as 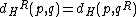 . Similarly, reverse-complement Hamming distance is
. Similarly, reverse-complement Hamming distance is 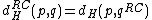 . (where
. (where 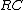 stands for reverse complement)
stands for reverse complement)Another important code design consideration linked to the process of oligonucleotide hybridization pertains to the GC content of sequences in a DNA code. The GC-content,
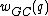 , of a DNA sequence
, of a DNA sequence 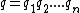 is defined to be the number of indices
is defined to be the number of indices 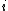 such that
such that 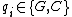 . A DNA code in which all codewords have the same GC-content,
. A DNA code in which all codewords have the same GC-content, 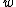 , is called a constant GC-content code.
, is called a constant GC-content code.A generalized Hadamard matrix
Hadamard matrix
In mathematics, an Hadamard matrix, named after the French mathematician Jacques Hadamard, is a square matrix whose entries are either +1 or −1 and whose rows are mutually orthogonal...
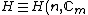 ) is an
) is an 

 square matrix with entries taken from the set of
square matrix with entries taken from the set of 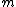 th roots of unity,
th roots of unity, 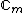 =
= 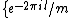 ,
,  = 0, ...,
= 0, ..., 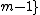 , that satisfies
, that satisfies  =
= 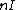 . Here
. Here  denotes the identity matrix of order
denotes the identity matrix of order  , while * stands for complex-congugation. We will only concern ourselves with the case
, while * stands for complex-congugation. We will only concern ourselves with the case 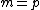 for some prime
for some prime 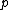 . A necessary condition for the existence of generalized Hadamard matrices
. A necessary condition for the existence of generalized Hadamard matrices 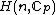 is that
is that 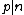 . The exponent matrix,
. The exponent matrix, 
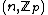 , of
, of 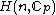 is the
is the 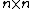 matrix with the entries in
matrix with the entries in  , is obtained by replacing each entry
, is obtained by replacing each entry 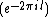 in
in 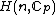 by the exponent
by the exponent  .
.The elements of the Hadamard exponent matrix lie in the Galois field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
 , and its row vectors constitute the codewords of what shall be called a generalized Hadamard code.
, and its row vectors constitute the codewords of what shall be called a generalized Hadamard code.Here, the elements of
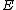 lie in the Galois field
lie in the Galois field 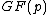 .
.By definition, a generalized Hadamard matrix
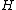 in its standard form has only 1s in its first row and column. The
in its standard form has only 1s in its first row and column. The 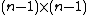 square matrix formed by the remaining entries of
square matrix formed by the remaining entries of 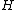 is called the core of
is called the core of 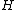 , and the corresponding submatrix of the exponent matrix
, and the corresponding submatrix of the exponent matrix  is called the core of construction. Thus, by omission of the all-zero first column cyclic generalized Hadamard codes are possible,
is called the core of construction. Thus, by omission of the all-zero first column cyclic generalized Hadamard codes are possible,whose codewords are the row vectors of the punctured matrix.
Also, the rows of such an exponent matrix satisfy the following two properties: (i) in each of the nonzero rows of the exponent matrix, each element of
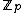 appears a constant number,
appears a constant number, 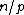 , of times; and (ii) the Hamming distance between any two rows is
, of times; and (ii) the Hamming distance between any two rows is 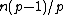 .
.Property U
Let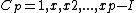 be the cyclic group generated by
be the cyclic group generated by  , where
, where 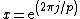 is a complex primitive
is a complex primitive 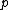 th root of unity, and
th root of unity, and 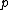 >
> 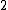 is a fixed prime. Further, let
is a fixed prime. Further, let 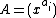 ,
, 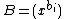 denote arbitrary vectors over
denote arbitrary vectors over 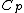 which are of length
which are of length  , where
, where  is a positive integer. Define the collection of differences between exponents
is a positive integer. Define the collection of differences between exponents  , where
, where 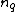 is the multiplicity of element
is the multiplicity of element  of
of  which appears in
which appears in 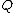 .
.Vector
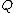 is said to satisfy Property U iff each element
is said to satisfy Property U iff each element 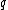 of
of 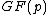 appears in
appears in 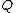 exactly
exactly  times (
times (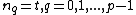 )
)The following lemma is of fundamental importance in constructing generalized Hadamard codes.
Lemma. Orthogonality of vectors over
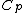 - For fixed primes
- For fixed primes 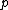 , arbitrary vectors
, arbitrary vectors 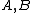 of length
of length 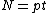 , whose elements are from
, whose elements are from  , are orthogonal if the vector
, are orthogonal if the vector 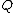 satisfies Property U, where
satisfies Property U, where  is the collection of
is the collection of  differences between the Hadamard exponents associated with
differences between the Hadamard exponents associated with 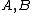 .
.M sequences
Let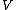 be an arbitrary vector of length
be an arbitrary vector of length 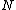 whose elements are in the finite field
whose elements are in the finite field 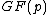 , where
, where  is a prime. Let the elements of vector
is a prime. Let the elements of vector  constitute the first period of an infinite sequence
constitute the first period of an infinite sequence  which is periodic of period
which is periodic of period 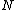 . If
. If 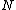 is the smallest period for conceiving a subsequence, the sequence is called an M-sequence, or a sequence of maximal least period obtained by cycling
is the smallest period for conceiving a subsequence, the sequence is called an M-sequence, or a sequence of maximal least period obtained by cycling 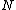 elements. If, when the elements of the ordered set
elements. If, when the elements of the ordered set  are permuted arbitrarily to yield
are permuted arbitrarily to yield 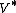 , the sequence
, the sequence  is an M-sequence, the sequence
is an M-sequence, the sequence  is called M-invariant.
is called M-invariant.The theorems that follow present conditions that ensure invariance in an M sequence. In conjunction with a certain uniformity property of
polynomial coeffecients, these conditions yield a simple method by which complex Hadamard matrices with cyclic core can be constructed.
The goal as outlined at the head of this article is to find cyclic matrix
 whose elements are in Galois field
whose elements are in Galois field 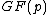 and whose dimension is
and whose dimension is 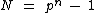 . The rows of
. The rows of 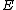 will be the nonzero codewords of a linear cyclic code
will be the nonzero codewords of a linear cyclic code 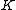 , if and only if there is polynomial
, if and only if there is polynomial 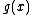 with coefficients in
with coefficients in 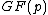 , which is a proper divisor of
, which is a proper divisor of  and which generates
and which generates 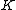 .
.In order to have
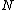 nonzero codewords,
nonzero codewords, 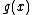 must be of degree
must be of degree 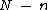 . Further, in order to generate a cyclic Hadamard core, the vector (of coefficients of)
. Further, in order to generate a cyclic Hadamard core, the vector (of coefficients of) 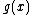 when operated upon with the cyclic shift operation must be of period
when operated upon with the cyclic shift operation must be of period 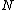 , and the vector difference of two arbitrary rows of
, and the vector difference of two arbitrary rows of 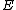 (augmented with zero) must satisfy the uniformity condition of Butson, previously referred to as Property U.
(augmented with zero) must satisfy the uniformity condition of Butson, previously referred to as Property U.One necessary condition for
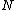 -peridoicity is that
-peridoicity is that 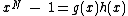 , where
, where  is monic irreducible
is monic irreducibleIrreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
over.
The approach here is to replace the last requirement with the condition that the coefficients of the vector
 be uniformly distributed over
be uniformly distributed over 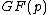 , each residue
, each residue  appears the same number of times (Property U). This heuristic approach has succeeded for all cases tried, and a proof that it always produces a cyclic core is given below.
appears the same number of times (Property U). This heuristic approach has succeeded for all cases tried, and a proof that it always produces a cyclic core is given below.Construction algorithm
Consider all monic irreducible polynomials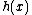 over
over 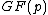 which are of degree
which are of degree  , and which permit a suitable companion
, and which permit a suitable companion 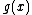 of degree
of degree 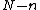 such that
such that 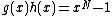 , where also vector
, where also vector 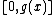 satisfies Property U. This requires only a simple computer algorithm for long division over
satisfies Property U. This requires only a simple computer algorithm for long division over 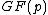 . Since
. Since 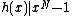 , the ideal generated by
, the ideal generated by 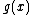 ,
, 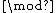
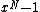 , will be a cyclic code
, will be a cyclic code 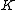 . Moreover, Property U guarantees the nonzero codewords form a cyclic matrix, each row being of period
. Moreover, Property U guarantees the nonzero codewords form a cyclic matrix, each row being of period 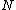 under cyclic permutation, which serves as a cyclic core
under cyclic permutation, which serves as a cyclic corefor Hadamard matrix
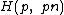 .
.As an example, a cyclic core for
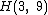 results from the companions
results from the companions 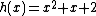 and
and 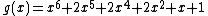 . The coefficients of
. The coefficients of 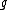 indicate that
indicate that 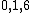 is the relative difference set,
is the relative difference set, 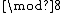 .
.Theorem
Let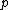 be a prime and
be a prime and 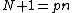 , with
, with 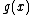 a monic polynomial of degree
a monic polynomial of degree 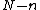 whose extended vector of coefficients
whose extended vector of coefficients 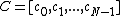 are elements of
are elements of  . The conditions are as follows:
. The conditions are as follows:(1) vector
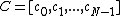 satisfies the property U explained above,
satisfies the property U explained above,(2)
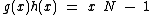 , where
, where 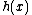 is a monic irreducible polynomial of degree
is a monic irreducible polynomial of degree  , guarantee the existence of a p-ary, linear cyclic code
, guarantee the existence of a p-ary, linear cyclic code 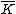 : of blocksize
: of blocksize 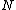 , such that the augmented code
, such that the augmented code 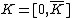 is the Hadamard exponent, for Hadamard matrix
is the Hadamard exponent, for Hadamard matrix 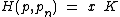 , with
, with 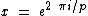 , where the core of
, where the core of 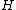 is cyclic matrix.
is cyclic matrix.Proof:
First, we note that since
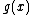 is monic, it divides
is monic, it divides 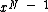 , and has degree =
, and has degree =  . Now, we need to show that the matrix
. Now, we need to show that the matrix  whose rows are the nonzero codewords, constitutes a cyclic core for some complex Hadamard matrix
whose rows are the nonzero codewords, constitutes a cyclic core for some complex Hadamard matrix 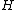 .
.Given: we know that
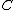 satisfies property U. Hence, all of the nonzero residues of
satisfies property U. Hence, all of the nonzero residues of 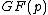 lie in C. By cycling through
lie in C. By cycling through  , we get the desired exponent matrix
, we get the desired exponent matrix 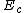 where we can get every codeword in
where we can get every codeword in  by cycling the first codeword. (This is because the sequence obtained by cycling through
by cycling the first codeword. (This is because the sequence obtained by cycling through 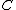 is an M-invariant sequence.)
is an M-invariant sequence.)We also see that augmentation of each codeword of
 by adding a leading zero element produces a vector which satisfies Property U. Also, since the code is linear, the
by adding a leading zero element produces a vector which satisfies Property U. Also, since the code is linear, the  vector difference of two arbitrary codewords is also a codeword and thus satisfy Property U. Therefore, the row vectors of the augmented code
vector difference of two arbitrary codewords is also a codeword and thus satisfy Property U. Therefore, the row vectors of the augmented code 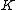 form a Hadamard exponent. Thus,
form a Hadamard exponent. Thus,  is the standard form of some complex Hadamard matrix
is the standard form of some complex Hadamard matrix 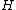 .
.Thus from the above property, we see that the core of
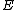 is a circulant matrix
is a circulant matrixCirculant matrix
In linear algebra, a circulant matrix is a special kind of Toeplitz matrix where each row vector is rotated one element to the right relative to the preceding row vector. In numerical analysis, circulant matrices are important because they are diagonalized by a discrete Fourier transform, and hence...
consisting of all the
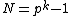 cyclic shifts of its first row. Such a core is called a cyclic core where in each element of
cyclic shifts of its first row. Such a core is called a cyclic core where in each element of 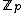 appears in each row of
appears in each row of 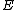 exactly
exactly 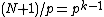 times, and the Hamming distance between any two rows is exactly
times, and the Hamming distance between any two rows is exactly 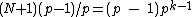 . The
. The 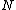 rows of the core
rows of the core 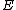 form a constant-composition code - one consisting of
form a constant-composition code - one consisting of  cyclic shifts of some length
cyclic shifts of some length 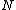 over the set
over the set 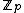 . Hamming distance between any two codewords in
. Hamming distance between any two codewords in 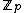 is
is 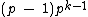 .
.The following can be inferred from the theorem as explained above. (For more detailed reading, the reader is referred to the paper by Heng and Cooke.)
Let
 for
for 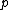 prime and
prime and 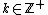 . Let
. Let 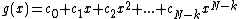 be a monic polynomial over
be a monic polynomial over 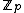 , of degree N - k such that
, of degree N - k such that 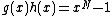 over
over 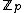 , for some monic irreducible polynomial
, for some monic irreducible polynomial 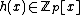 . Suppose that the vector
. Suppose that the vector  , with
, with 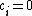 for (N - k) < i < N, has the property that it contains each element of
for (N - k) < i < N, has the property that it contains each element of  the same number of times. Then, the
the same number of times. Then, the 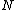 cyclic shifts of the vector
cyclic shifts of the vector 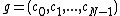 form the core of the exponent matrix of some Hadamard matrix .
form the core of the exponent matrix of some Hadamard matrix .DNA codes with constant GC-content can obviously be constructed from constant-composition codes (A constant composition code over a k-ary alphabet has the property that the numbers of occurrences of the k symbols within a codeword is the same for each codeword) over
 by mapping the symbols of
by mapping the symbols of  to the symbols of the DNA alphabet,
to the symbols of the DNA alphabet, 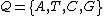 . For example, using cyclic constant composition code of length
. For example, using cyclic constant composition code of length  over
over 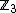 guaranteed by the theorem proved above and the resulting property, and using the mapping that takes
guaranteed by the theorem proved above and the resulting property, and using the mapping that takes 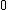 to
to  ,
, 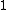 to
to 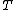 and
and 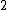 to
to  , we obtain a DNA code
, we obtain a DNA code 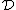 with
with 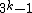 and a GC-content of
and a GC-content of 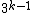 . Clearly
. Clearly 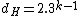 and in fact since
and in fact since 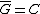 and no codeword in
and no codeword in 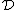 contains no symbol
contains no symbol 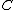 , we also have
, we also have 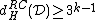 .
.This is summarized in the following corollary.
Corollary
For any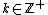 , there exists DNA codes
, there exists DNA codes 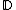 with
with 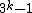 codewords of length
codewords of length  , constant GC-content
, constant GC-content 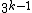 ,
,  and in which every codeword is a cyclic shift of a fixed generator codeword
and in which every codeword is a cyclic shift of a fixed generator codeword 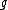 .
.Each of the following vectors generates a cyclic core of a Hadamard matrix
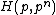 (where
(where 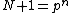 , and
, and 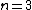 in this example) :
in this example) :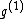 =
= 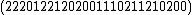 ;
; =
= 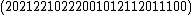 .
.Where,
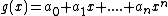 .
.Thus, we see how DNA codes can be obtained from such generators by mapping
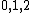 onto
onto 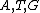 . The actual choice of mapping plays a major role in secondary structure formations in the codewords.
. The actual choice of mapping plays a major role in secondary structure formations in the codewords.We see that all such mappings yield codes with essentially the same parameters. However the actual choice of mapping has a strong influence on the secondary structure of the codewords. For example, the codeword illustrated was obtained from
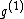 via the mapping
via the mapping 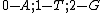 , while the codeword
, while the codeword 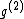 was obtained from the same generator
was obtained from the same generator 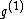 via the mapping
via the mapping 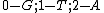 .
.2. Code construction via a Binary Mapping
Perhaps a simpler approach to building/designing DNA codewords is by having a binary mapping by looking at the design problem as that of constructing the codewords as binary codes. i.e. map the DNA codeword alphabet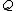 onto the set of 2-bit length binary words as shown:
onto the set of 2-bit length binary words as shown: 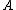 ->
-> 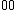 ,
, 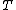 ->
-> 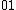 ,
, 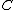 ->
-> 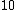 ,
, 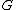 ->
-> .
.As we can see, the first bit of a binary image clearly determines which complementary pair it belongs to.
Let
 be a DNA sequence. The sequence
be a DNA sequence. The sequence 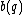 obtained by applying the mapping given above to
obtained by applying the mapping given above to 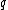 , is called the binary image of
, is called the binary image of 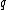 .
.Now, let
 =
= 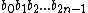 .
.Now, let the subsequence
 =
= 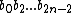 be called the even subsequence of
be called the even subsequence of  , and
, and 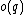 =
= 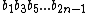 be called the odd subsequence of
be called the odd subsequence of 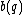 .
.Thus, for example, for
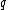 =
= 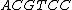 , then,
, then, 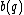 =
= 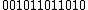 .
.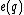 will then be =
will then be = 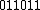 and
and 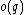 =
=  .
.Let us define an even component as
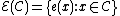 , and an odd component as
, and an odd component as  .
.From this choice of binary mapping, the GC-content of DNA sequence
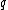 = Hamming weight of
= Hamming weight of 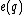 .
.Hence, a DNA code
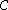 is a constant GC-content codeword if and only if its even component
is a constant GC-content codeword if and only if its even component 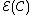 is a constant-weight code.
is a constant-weight code.Let
 be a binary code consisting of
be a binary code consisting of 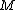 codewords of length
codewords of length  and minimum distance
and minimum distance 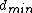 , such that
, such that 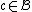 implies that
implies that 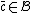 .
.For
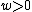 , consider the constant-weight subcode
, consider the constant-weight subcode 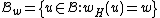 , where
, where 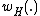 denotes Hamming weight.
denotes Hamming weight.Choose
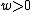 such that
such that 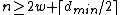 , and consider a DNA code,
, and consider a DNA code, 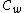 , with the following choice for its even and odd components:
, with the following choice for its even and odd components: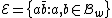 ,
, 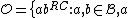 <
<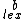
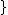 .
.Where <
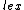 denotes lexicographic ordering. The
denotes lexicographic ordering. The  <
< 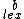 in the definition of
in the definition of  ensures that if
ensures that if 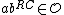 , then
, then 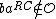 , so that distinct codewords in
, so that distinct codewords in  cannot be reverse-complements of each other.
cannot be reverse-complements of each other.The code
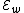 has
has 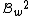 codewords of length
codewords of length 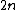 and constant weight
and constant weight  .
.Furthermore,
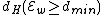 and
and 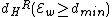 ( this is because
( this is because 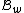 is a subset of the codewords in
is a subset of the codewords in 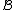 ).
).Also,
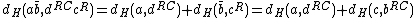 .
.Note that
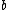 and
and  both have weight
both have weight 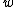 . This implies that
. This implies that 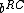 and
and 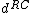 have weight
have weight  .
.And due to the weight constraint on
 , we must have for all
, we must have for all 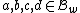 ,
, .
.Thus, the code
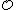 has
has  codewords of length
codewords of length 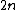 .
.From this, we see that

(because of the fact that the component codewords of
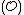 are taken from
are taken from 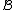 ).
).Similarly,
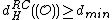 .
.Therefore, the DNA code
with
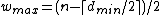 , has
, has 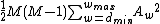 codewords of length
codewords of length  ,
,and satisfies
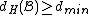
and
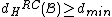 .
.From the examples listed above, one can wonder what could be the future potential of DNA-based computers?
Despite its enormous potential, this method is highly unlikely to be implemented in home computers or even computers at offices, etc. because of the sheer flexibility and speed as well as cost factors that favor silicon chip based devices used for the computers today.
However, such a method could be used in situations where the only available method is this and requires the accuracy associated with the DNA hybridization mechanism; applications which require operations to be performed with a high degree of reliability.
Currently, there are several software packages, such as the Vienna package, which can predict secondary structure formations in single stranded DNAs (i.e. oligonucleotides) or RNA sequences.