
D'Alembert operator
Encyclopedia
In special relativity
, electromagnetism
and wave theory
, the d'Alembert operator (represented by a box: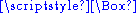 ), also called the d'Alembertian or the wave operator, is the Laplace operator
), also called the d'Alembertian or the wave operator, is the Laplace operator
of Minkowski space
. The operator is named for French mathematician and physicist Jean le Rond d'Alembert
. In Minkowski space in standard coordinates (t, x, y, z) it has the form:
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
and wave theory
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
, the d'Alembert operator (represented by a box:
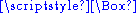 ), also called the d'Alembertian or the wave operator, is the Laplace operator
), also called the d'Alembertian or the wave operator, is the Laplace operatorLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
of Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
. The operator is named for French mathematician and physicist Jean le Rond d'Alembert
Jean le Rond d'Alembert
Jean-Baptiste le Rond d'Alembert was a French mathematician, mechanician, physicist, philosopher, and music theorist. He was also co-editor with Denis Diderot of the Encyclopédie...
. In Minkowski space in standard coordinates (t, x, y, z) it has the form:
-
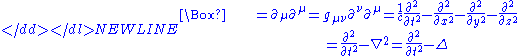
Here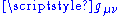 is the Minkowski metric with
is the Minkowski metric with 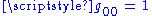 ,
, 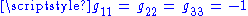 ,
, 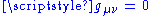 for
for  . Note that the μ and ν summation indices range from 0 to 3: see Einstein notationEinstein notationIn mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
. Note that the μ and ν summation indices range from 0 to 3: see Einstein notationEinstein notationIn mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
. We have assumed units such that the speed of light . Some authors also use the negative metric signatureMetric signatureThe signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
. Some authors also use the negative metric signatureMetric signatureThe signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
of [− + + +] with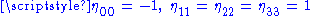 .
.
Lorentz transformationLorentz transformationIn physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s leave the Minkowski metric invariant, so the d'Alembertian is a Lorentz scalarLorentz scalarIn physics, a Lorentz scalar is a scalar which is invariant under a Lorentz transformation. A Lorentz scalar may be generated from multiplication of vectors or tensors...
. The above coordinate expressions remain valid for the standard coordinates in every inertial frame.
Alternate notations
There are a variety of notations for the d'Alembertian. The most common is the symbol : the four sides of the box representing the four dimensions of space-time and the
: the four sides of the box representing the four dimensions of space-time and the  which emphasizes the scalar property through the squared term (much like the Laplacian). This symbol is sometimes called the quabla (cf. nabla symbolNabla symbolright|thumb|256px|The [[harp]], the instrument after which the nabla symbol is namedNabla is the symbol \nabla . The name comes from the Greek word for a Hebrew harp, which had a similar shape. Related words also exist in Aramaic and Hebrew. The symbol was first used by William Rowan Hamilton in...
which emphasizes the scalar property through the squared term (much like the Laplacian). This symbol is sometimes called the quabla (cf. nabla symbolNabla symbolright|thumb|256px|The [[harp]], the instrument after which the nabla symbol is namedNabla is the symbol \nabla . The name comes from the Greek word for a Hebrew harp, which had a similar shape. Related words also exist in Aramaic and Hebrew. The symbol was first used by William Rowan Hamilton in...
). In keeping with the triangular notation for the Laplacian sometimes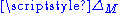 is used.
is used.
Another way to write the d'Alembertian in flat standard coordinates is . This notation is used extensively in quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. This notation is used extensively in quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
where partial derivatives are usually indexed: so the lack of an index with the squared partial derivative signals the presence of the D'Alembertian.
Sometimes is used to represent the four-dimensional Levi-Civita covariant derivativeCovariant derivativeIn mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
is used to represent the four-dimensional Levi-Civita covariant derivativeCovariant derivativeIn mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
. The symbol is then used to represent the space derivatives, but this is coordinate chart dependent.
is then used to represent the space derivatives, but this is coordinate chart dependent.
Applications
The Klein–Gordon equation has the form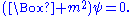
The wave equationWave equationThe wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
for the electromagnetic field in vacuum is
- where
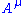 is the electromagnetic four-potentialElectromagnetic four-potentialThe electromagnetic four-potential is a potential from which the electromagnetic field can be derived. It combines both the electric scalar potential and the magnetic vector potential into a single space-time four-vector. In a given reference frame, the first component is the scalar potential and...
is the electromagnetic four-potentialElectromagnetic four-potentialThe electromagnetic four-potential is a potential from which the electromagnetic field can be derived. It combines both the electric scalar potential and the magnetic vector potential into a single space-time four-vector. In a given reference frame, the first component is the scalar potential and...
.
The wave equationWave equationThe wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
for small vibrations is of the form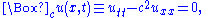
- where
 is the displacement.
is the displacement.
Green's function
The Green's functionGreen's functionIn mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
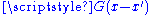 for the d'Alembertian is defined by the equation
for the d'Alembertian is defined by the equation
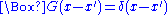
where is the Dirac delta functionDirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
is the Dirac delta functionDirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
and and
and 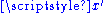 are two points in Minkowski space.
are two points in Minkowski space.
Explicitly we have
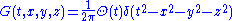
where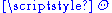 is the Heaviside step functionHeaviside step functionThe Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
is the Heaviside step functionHeaviside step functionThe Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
. - where

