
Curvature invariant
Encyclopedia
In Riemannian geometry
and pseudo-Riemannian geometry, curvature invariants are scalar
quantities constructed from tensors that represent curvature
. These tensors are usually the Riemann tensor, the Weyl tensor
, the Ricci tensor and tensors formed from these by the operations of taking dual
s, contractions and covariant differentiations.
The Riemann tensor is a multilinear operator of fourth rank acting on tangent vector
s. However, it can also be considered a linear operator acting on bivector
s, and as such it has a characteristic polynomial
, whose coefficients and roots (eigenvalues) are polynomial scalar invariants.
, curvature scalars play an important role in telling distinct spacetimes apart.
Two of the most basic curvature invariants in general relativity are the Kretschmann scalar

and the Chern–Pontryagin scalar,
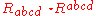
These are analogous to two familiar quadratic invariants of the electromagnetic field tensor in classical electromagnetism.
An important unsolved problem in general relativity is to give a basis
(and any syzygies
) for the zero-th order invariants of the Riemann tensor.
They have limitations because many distinct spacetimes cannot be distinguished on this basis. In particular, so called VSI spacetime
s (including pp-waves as well as some other Petrov type N and III spacetimes) cannot be distinguished from Minkowski spacetime using any number of curvature invariants (of any order).
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
and pseudo-Riemannian geometry, curvature invariants are scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
quantities constructed from tensors that represent curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
. These tensors are usually the Riemann tensor, the Weyl tensor
Weyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
, the Ricci tensor and tensors formed from these by the operations of taking dual
Dual
Dual may refer to:* Dual , a notion of paired concepts that mirror one another** Dual , a formalization of mathematical duality** . . ...
s, contractions and covariant differentiations.
Types of curvature invariants
The invariants most often considered are polynomial invariants. These are polynomials constructed from contractions such as traces. Second degree examples are called quadratic invariants, and so forth. Invariants constructed using covariant derivatives up to order n are called n-th order differential invariants.The Riemann tensor is a multilinear operator of fourth rank acting on tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
s. However, it can also be considered a linear operator acting on bivector
Bivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
s, and as such it has a characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
, whose coefficients and roots (eigenvalues) are polynomial scalar invariants.
Physical applications
In metric theories of gravitation such as general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, curvature scalars play an important role in telling distinct spacetimes apart.
Two of the most basic curvature invariants in general relativity are the Kretschmann scalar

and the Chern–Pontryagin scalar,
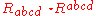
These are analogous to two familiar quadratic invariants of the electromagnetic field tensor in classical electromagnetism.
An important unsolved problem in general relativity is to give a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
(and any syzygies
Syzygy (mathematics)
In mathematics, a syzygy is a relation between the generators of a module M. The set of all such relations is called the "first syzygy module of M". A relation between generators of the first syzygy module is called a "second syzygy" of M, and the set of all such relations is called the...
) for the zero-th order invariants of the Riemann tensor.
They have limitations because many distinct spacetimes cannot be distinguished on this basis. In particular, so called VSI spacetime
VSI spacetime
In mathematical physics, VSI spacetimes are Lorentzian manifolds with all polynomial curvature invariants of all orders vanishing. An example with this property in four dimensions is a pp-wave. VSI spacetimes however also contain some other four-dimensional Kundt spacetimes of Petrov type N and III...
s (including pp-waves as well as some other Petrov type N and III spacetimes) cannot be distinguished from Minkowski spacetime using any number of curvature invariants (of any order).
See also
- Cartan–Karlhede algorithm
- Carminati–McLenaghan invariants
- Curvature invariant (general relativity)Curvature invariant (general relativity)Curvature invariants in general relativity are a set of scalars called curvature invariants that arise in general relativity. They are formed from the Riemann, Weyl and Ricci tensors - which represent curvature - and possibly operations on them such as contraction, covariant differentiation and...
- Ricci decompositionRicci decompositionIn semi-Riemannian geometry, the Ricci decomposition is a way of breaking up the Riemann curvature tensor of a pseudo-Riemannian manifold into pieces with useful individual algebraic properties...

