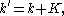Crystal momentum
Encyclopedia
In solid-state physics
crystal momentum or quasimomentum is a momentum-like vector associated with electron
s in a crystal lattice
. It is defined by the associated wave vectors
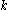 of this lattice, according to
of this lattice, according to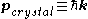
(where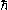 is the reduced Planck's constant).
is the reduced Planck's constant).
Like regular momentum, crystal momentum frequently exhibits the property of being conserved, and is thus extraordinarily useful to physicists and materials scientists as an analytical tool.
particles traveling through a fixed infinite periodic potential such that
such that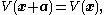
where is an arbitrary lattice vector. Such a model is sensible because (a) crystal ions that actually form the lattice structure are typically on the order of tens of thousands of times more massive than electrons
is an arbitrary lattice vector. Such a model is sensible because (a) crystal ions that actually form the lattice structure are typically on the order of tens of thousands of times more massive than electrons
,
making it safe to replace them with a fixed potential structure, and (b) the macroscopic dimensions of a crystal are typically far greater than a single lattice spacing, making edge effects negligible. A consequence of this potential energy function is that it is possible to shift the initial position of an electron by any lattice vector without changing any aspect of the problem, thereby defining a discrete symmetry. (Speaking more technically, an infinite periodic potential implies that the lattice translation operator
without changing any aspect of the problem, thereby defining a discrete symmetry. (Speaking more technically, an infinite periodic potential implies that the lattice translation operator 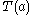 commutes
commutes
with the Hamiltonian
, assuming a simple kinetic-plus-potential form.)
These conditions imply Bloch's theorem
, which states in terms of equations that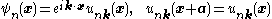 ,
,
or in terms of words that an electron in a lattice, which can be modeled as a single particle wave function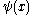 , finds its stationary state solutions in the form of a plane wave multiplied by a periodic function
, finds its stationary state solutions in the form of a plane wave multiplied by a periodic function 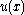 . The theorem arises as a direct consequence of the aforementioned fact that the lattice symmetry translation operator commutes with the system's Hamiltonian.
. The theorem arises as a direct consequence of the aforementioned fact that the lattice symmetry translation operator commutes with the system's Hamiltonian.
One of the notable aspects of Bloch's theorem is that it shows directly that steady state solutions may be identified with a wave vector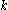 , meaning that this quantum number
, meaning that this quantum number
remains a constant of motion. Crystal momentum is then conventionally defined by multiplying this wave vector by Planck's constant: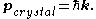
While this is in fact identical to the definition one might give for regular momentum (for example, by treating the effects of the translation operator by the effects of a particle in free space
),
there are important theoretical differences. For example, while regular momentum is completely conserved, crystal momentum is only conserved to within a lattice vector, i.e., an electron can be described not only by the wave vector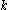 , but also with any other wave vector k' such that
, but also with any other wave vector k' such that
where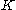 is an arbitrary reciprocal lattice
is an arbitrary reciprocal lattice
vector.
This is a consequence of the fact that the lattice symmetry is discrete as opposed to continuous, and thus its associated conservation law cannot be derived using Noether's theorem
.
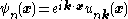 is the same as that of a free particle with momentum
is the same as that of a free particle with momentum 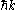 , i.e.
, i.e.  gives the state's periodicity, which is not the same as that of the lattice. This modulation contributes to the kinetic energy of the particle (whereas the modulation is entirely responsible for the kinetic energy of a free particle).
gives the state's periodicity, which is not the same as that of the lattice. This modulation contributes to the kinetic energy of the particle (whereas the modulation is entirely responsible for the kinetic energy of a free particle).
In regions where the band is approximately parabolic the crystal momentum is equal to the momentum of a free particle with momentum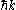 if we assign the particle an effective mass
if we assign the particle an effective mass
that's related to the curvature of the parabola.
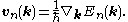
This is the same formula as the group velocity of a wave
. Because this has nonzero velocity solutions, it implies that any crystal structure containing electrons should be a perfect conductor
.
In an infinite perfect crystal, an electron can travel forever in the same direction, without ever colliding with the atoms in the crystal. In practice, however, crystals conductivity is finite because crystals are not perfect. Electrons can collide with and scatter
from anything that alters the perfect periodic structure of the crystal, most commonly, crystallographic defect
s, the crystal surface, and random thermal vibrations of the atoms in the crystal (phonon
s).
Nevertheless, if one looks sufficiently deeply within the crystal on a short enough distance scale, these solutions form a valid approximation and one really can visualize Bloch electrons as crystal momentum eigenstates passing through a crystal at finite nonzero velocity.
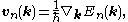
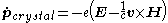
Here perhaps the analogy between crystal momentum and true momentum is at its most powerful, for these are precisely the equations that a free space electron obeys in the absence of any crystal structure. Crystal momentum also earns its chance to shine in these types of calculations, for, in order to calculate an electron's trajectory of motion using the above equations one need only consider external fields, while attempting the calculation from a set of EOMs based on true momentum would require taking into account individual coulomb and Lorenz forces of every single lattice ion in addition to the external field.
), irradiating light on a crystal sample results in the ejection of an electron away from the crystal. Throughout the course of the interaction, one is allowed to conflate the two concepts of crystal and true momentum and thereby gain direct knowledge of a crystal's band structure. That is to say, an electron's crystal momentum inside the crystal becomes its true momentum after it leaves, and the true momentum may be subsequently inferred from the equation
by measuring the angle and kinetic energy at which the electron exits the crystal (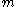 is a single electron's mass). Interestingly, because crystal symmetry in the direction normal to the crystal surface is lost at the crystal boundary, crystal momentum in this direction is not conserved. Consequently, the only directions in which useful ARPES data can be gleaned are directions parallel to the crystal surface.
is a single electron's mass). Interestingly, because crystal symmetry in the direction normal to the crystal surface is lost at the crystal boundary, crystal momentum in this direction is not conserved. Consequently, the only directions in which useful ARPES data can be gleaned are directions parallel to the crystal surface.
Solid-state physics
Solid-state physics is the study of rigid matter, or solids, through methods such as quantum mechanics, crystallography, electromagnetism, and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the large-scale properties of solid materials result from...
crystal momentum or quasimomentum is a momentum-like vector associated with electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s in a crystal lattice
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
. It is defined by the associated wave vectors
Reciprocal lattice
In physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
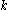 of this lattice, according to
of this lattice, according to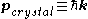
(where
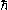 is the reduced Planck's constant).
is the reduced Planck's constant).Like regular momentum, crystal momentum frequently exhibits the property of being conserved, and is thus extraordinarily useful to physicists and materials scientists as an analytical tool.
Lattice symmetry origins
A common method of modeling crystal structure and behavior is to view electrons as quantum mechanicalQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
particles traveling through a fixed infinite periodic potential
 such that
such that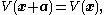
where
 is an arbitrary lattice vector. Such a model is sensible because (a) crystal ions that actually form the lattice structure are typically on the order of tens of thousands of times more massive than electrons
is an arbitrary lattice vector. Such a model is sensible because (a) crystal ions that actually form the lattice structure are typically on the order of tens of thousands of times more massive than electrons,
making it safe to replace them with a fixed potential structure, and (b) the macroscopic dimensions of a crystal are typically far greater than a single lattice spacing, making edge effects negligible. A consequence of this potential energy function is that it is possible to shift the initial position of an electron by any lattice vector
 without changing any aspect of the problem, thereby defining a discrete symmetry. (Speaking more technically, an infinite periodic potential implies that the lattice translation operator
without changing any aspect of the problem, thereby defining a discrete symmetry. (Speaking more technically, an infinite periodic potential implies that the lattice translation operator 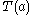 commutes
commutesCommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
with the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
, assuming a simple kinetic-plus-potential form.)
These conditions imply Bloch's theorem
Bloch wave
A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle placed in a periodic potential...
, which states in terms of equations that
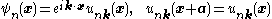 ,
,or in terms of words that an electron in a lattice, which can be modeled as a single particle wave function
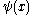 , finds its stationary state solutions in the form of a plane wave multiplied by a periodic function
, finds its stationary state solutions in the form of a plane wave multiplied by a periodic function 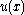 . The theorem arises as a direct consequence of the aforementioned fact that the lattice symmetry translation operator commutes with the system's Hamiltonian.
. The theorem arises as a direct consequence of the aforementioned fact that the lattice symmetry translation operator commutes with the system's Hamiltonian.One of the notable aspects of Bloch's theorem is that it shows directly that steady state solutions may be identified with a wave vector
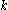 , meaning that this quantum number
, meaning that this quantum numberQuantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
remains a constant of motion. Crystal momentum is then conventionally defined by multiplying this wave vector by Planck's constant:
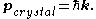
While this is in fact identical to the definition one might give for regular momentum (for example, by treating the effects of the translation operator by the effects of a particle in free space
),
there are important theoretical differences. For example, while regular momentum is completely conserved, crystal momentum is only conserved to within a lattice vector, i.e., an electron can be described not only by the wave vector
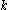 , but also with any other wave vector k' such that
, but also with any other wave vector k' such that
where
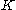 is an arbitrary reciprocal lattice
is an arbitrary reciprocal latticeReciprocal lattice
In physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
vector.
This is a consequence of the fact that the lattice symmetry is discrete as opposed to continuous, and thus its associated conservation law cannot be derived using Noether's theorem
Noether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
.
Physical significance
The phase modulation of the Bloch state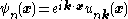 is the same as that of a free particle with momentum
is the same as that of a free particle with momentum 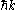 , i.e.
, i.e.  gives the state's periodicity, which is not the same as that of the lattice. This modulation contributes to the kinetic energy of the particle (whereas the modulation is entirely responsible for the kinetic energy of a free particle).
gives the state's periodicity, which is not the same as that of the lattice. This modulation contributes to the kinetic energy of the particle (whereas the modulation is entirely responsible for the kinetic energy of a free particle).In regions where the band is approximately parabolic the crystal momentum is equal to the momentum of a free particle with momentum
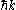 if we assign the particle an effective mass
if we assign the particle an effective massEffective mass
In solid state physics, a particle's effective mass is the mass it seems to carry in the semiclassical model of transport in a crystal. It can be shown that electrons and holes in a crystal respond to electric and magnetic fields almost as if they were particles with a mass dependence in their...
that's related to the curvature of the parabola.
Nonzero steady velocity
Crystal momentum corresponds to the physically measurable concept of velocity according to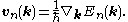
This is the same formula as the group velocity of a wave
Group velocity
The group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space....
. Because this has nonzero velocity solutions, it implies that any crystal structure containing electrons should be a perfect conductor
Perfect conductor
A perfect conductor is an electrical conductor with no resistivity. The concept is used to model systems in which the electrical resistance or resistivity is negligible compared to other effects. One such model is ideal magnetohydrodynamics, the study of perfectly conductive fluids...
.
In an infinite perfect crystal, an electron can travel forever in the same direction, without ever colliding with the atoms in the crystal. In practice, however, crystals conductivity is finite because crystals are not perfect. Electrons can collide with and scatter
Electron scattering
Electron scattering is the process whereby an electron is deflected from its original trajectory. As they are charged particles, they are subject to electromagnetic forces.-Phenomena:...
from anything that alters the perfect periodic structure of the crystal, most commonly, crystallographic defect
Crystallographic defect
Crystalline solids exhibit a periodic crystal structure. The positions of atoms or molecules occur on repeating fixed distances, determined by the unit cell parameters. However, the arrangement of atom or molecules in most crystalline materials is not perfect...
s, the crystal surface, and random thermal vibrations of the atoms in the crystal (phonon
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
s).
Nevertheless, if one looks sufficiently deeply within the crystal on a short enough distance scale, these solutions form a valid approximation and one really can visualize Bloch electrons as crystal momentum eigenstates passing through a crystal at finite nonzero velocity.
Response to electric and magnetic fields
Crystal momentum also plays a seminal role in the Semiclassical model of electron dynamics, where it obeys the equations of motion (in cgs units)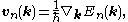
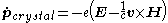
Here perhaps the analogy between crystal momentum and true momentum is at its most powerful, for these are precisely the equations that a free space electron obeys in the absence of any crystal structure. Crystal momentum also earns its chance to shine in these types of calculations, for, in order to calculate an electron's trajectory of motion using the above equations one need only consider external fields, while attempting the calculation from a set of EOMs based on true momentum would require taking into account individual coulomb and Lorenz forces of every single lattice ion in addition to the external field.
ARPES
In angle resolved photo-emission spectroscopy (ARPESARPES
Angle-resolved photoemission spectroscopy , also known as ARUPS , is a direct experimental technique to observe the distribution of the electrons in the reciprocal space of solids...
), irradiating light on a crystal sample results in the ejection of an electron away from the crystal. Throughout the course of the interaction, one is allowed to conflate the two concepts of crystal and true momentum and thereby gain direct knowledge of a crystal's band structure. That is to say, an electron's crystal momentum inside the crystal becomes its true momentum after it leaves, and the true momentum may be subsequently inferred from the equation

by measuring the angle and kinetic energy at which the electron exits the crystal (
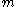 is a single electron's mass). Interestingly, because crystal symmetry in the direction normal to the crystal surface is lost at the crystal boundary, crystal momentum in this direction is not conserved. Consequently, the only directions in which useful ARPES data can be gleaned are directions parallel to the crystal surface.
is a single electron's mass). Interestingly, because crystal symmetry in the direction normal to the crystal surface is lost at the crystal boundary, crystal momentum in this direction is not conserved. Consequently, the only directions in which useful ARPES data can be gleaned are directions parallel to the crystal surface.