Cramer-von-Mises criterion
Encyclopedia
In statistics
the Cramér–von Mises criterion is a criterion used for judging the goodness of fit
of a cumulative distribution function
compared to a given empirical distribution function
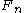, or for comparing two empirical distributions. It is also used as a part of other algorithms, such as minimum distance estimation
. It is defined as
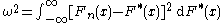
In one-sample applications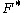
is the theoretical distribution and 
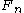is the empirically observed distribution
. Alternatively the two distributions can both be empirically estimated ones; this is called the two-sample case.
The criterion is named after Harald Cramér
and Richard Edler von Mises
who first proposed it in 1928-1930. The generalization to two samples is due to Anderson
.
The Cramér–von Mises test is an alternative to the Kolmogorov-Smirnov test
.
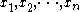be the observed values, in increasing order. Then the statistic is
If this value is larger than the tabulated value the hypothesis that the data come from the distribution
can be rejected.
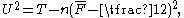
where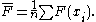
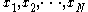and 
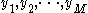be the observed values in the first and second sample respectively, in increasing order. Let 
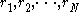be the ranks of the x's in the combined sample, and let 
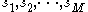be the ranks of the y's in the combined sample. Anderson shows that
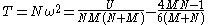
where U is defined as
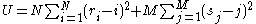
If the value of T is larger than the tabulated values, the hypothesis that the two samples come from the same distribution can be rejected. (Some books give critical values for U, which is more convenient, as it avoids the need to compute T via the expression above. The conclusion will be the same).
The above assumes there are no duplicates in the
, 
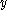, and 
sequences. So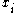 
is unique, and its rank is 
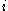in the sorted list 
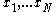. If there are duplicates, and 
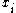through 
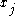are a run of identical values in the sorted list, then one common approach is the midrank method: assign each duplicate a "rank" of 
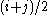. In the above equations, in the expressions 
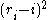and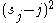 
, duplicates can modify all four variables 
, 
, 
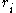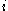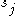, and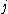 
.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
the Cramér–von Mises criterion is a criterion used for judging the goodness of fit
Goodness of fit
The goodness of fit of a statistical model describes how well it fits a set of observations. Measures of goodness of fit typically summarize the discrepancy between observed values and the values expected under the model in question. Such measures can be used in statistical hypothesis testing, e.g...
of a cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
compared to a given empirical distribution functionEmpirical distribution function
In statistics, the empirical distribution function, or empirical cdf, is the cumulative distribution function associated with the empirical measure of the sample. This cdf is a step function that jumps up by 1/n at each of the n data points. The empirical distribution function estimates the true...
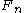, or for comparing two empirical distributions. It is also used as a part of other algorithms, such as minimum distance estimationMinimum distance estimation
Minimum distance estimation is a statistical method for fitting a mathematical model to data, usually the empirical distribution.-Definition:...
. It is defined as
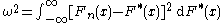
In one-sample applications
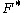is the theoretical distribution and 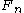is the empirically observed distributionEmpirical distribution function
In statistics, the empirical distribution function, or empirical cdf, is the cumulative distribution function associated with the empirical measure of the sample. This cdf is a step function that jumps up by 1/n at each of the n data points. The empirical distribution function estimates the true...
. Alternatively the two distributions can both be empirically estimated ones; this is called the two-sample case.
The criterion is named after Harald Cramér
Harald Cramér
Harald Cramér was a Swedish mathematician, actuary, and statistician, specializing in mathematical statistics and probabilistic number theory. He was once described by John Kingman as "one of the giants of statistical theory".-Early life:Harald Cramér was born in Stockholm, Sweden on September...
and Richard Edler von Mises
Richard Edler von Mises
Richard Edler von Mises was a scientist and mathematician who worked on solid mechanics, fluid mechanics, aerodynamics, aeronautics, statistics and probability theory. He held the position of Gordon-McKay Professor of Aerodynamics and Applied Mathematics at Harvard University...
who first proposed it in 1928-1930. The generalization to two samples is due to Anderson
Theodore Wilbur Anderson
Theodore Wilbur Anderson is an American mathematician and statistician who has specialized in the analysis of multivariate data.Born in Minneapolis, Minnesota, he was awarded a Guggenheim Fellowship in 1946....
.
The Cramér–von Mises test is an alternative to the Kolmogorov-Smirnov test
Kolmogorov-Smirnov test
In statistics, the Kolmogorov–Smirnov test is a nonparametric test for the equality of continuous, one-dimensional probability distributions that can be used to compare a sample with a reference probability distribution , or to compare two samples...
.
Cramér–von Mises test (one sample)
Let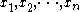 be the observed values, in increasing order. Then the statistic isIf this value is larger than the tabulated value the hypothesis that the data come from the distribution
can be rejected.Watson test
A modified version of the Cramér–von Mises test is the Watson test which uses the statistic U2, where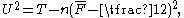where
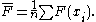
Cramér–von Mises test (two samples)
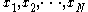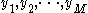Let and be the observed values in the first and second sample respectively, in increasing order. Let 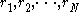be the ranks of the x's in the combined sample, and let 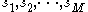be the ranks of the y's in the combined sample. Anderson shows that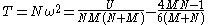where U is defined as
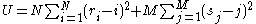
If the value of T is larger than the tabulated values, the hypothesis that the two samples come from the same distribution can be rejected. (Some books give critical values for U, which is more convenient, as it avoids the need to compute T via the expression above. The conclusion will be the same).
The above assumes there are no duplicates in the
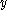, , and sequences. So 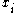is unique, and its rank is 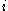in the sorted list 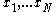. If there are duplicates, and 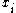through 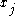are a run of identical values in the sorted list, then one common approach is the midrank method: assign each duplicate a "rank" of 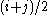. In the above equations, in the expressions 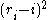and 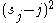, duplicates can modify all four variables 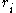, , 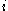, 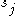and 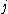.External links
- C-vM Two Sample Test (Documentation for performing the test using RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
- Table of Critical values for 1 sample CvM test